
 ∥
∥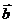 (
(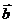 ¹
¹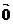 )的充要条件是x1y2-x2y1=0
)的充要条件是x1y2-x2y1=0
设 =(x1, y1) ,
=(x1, y1) ,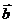 =(x2, y2) 其中
=(x2, y2) 其中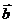 ¹
¹ .
.
由 =λ
=λ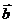 得,
(x1, y1)
=λ(x2, y2)
得,
(x1, y1)
=λ(x2, y2) 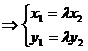 消去λ,x1y2-x2y1=0
消去λ,x1y2-x2y1=0
探究:(1)消去λ时不能两式相除,∵y1, y2有可能为0, ∵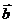 ¹
¹ ∴x2, y2中至少有一个不为0
∴x2, y2中至少有一个不为0
(2)充要条件不能写成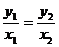 ∵x1, x2有可能为0
∵x1, x2有可能为0
(3)从而向量共线的充要条件有两种形式: ∥
∥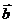 (
(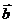 ¹
¹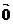 )
)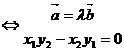
2.平面向量的坐标运算
若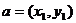 ,
,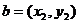 ,
,
则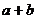
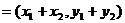 ,
,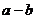
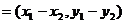 ,
,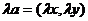 .
.
若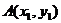 ,
,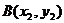 ,则
,则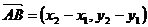
1.平面向量的坐标表示
 分别取与
分别取与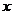 轴、
轴、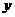 轴方向相同的两个单位向量
轴方向相同的两个单位向量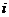 、
、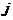 作为基底.任作一个向量
作为基底.任作一个向量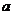 ,由平面向量基本定理知,有且只有一对实数
,由平面向量基本定理知,有且只有一对实数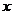 、
、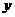 ,使得
,使得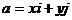
把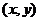 叫做向量
叫做向量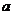 的(直角)坐标,记作
的(直角)坐标,记作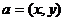
其中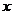 叫做
叫做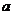 在
在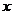 轴上的坐标,
轴上的坐标,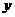 叫做
叫做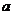 在
在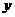 轴上的坐标, 特别地,
轴上的坐标, 特别地,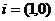 ,
,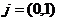 ,
,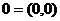 .
.
(王海)
第6课时
§2.3.4 平面向量共线的坐标表示
教学目的:
(1)理解平面向量的坐标的概念;
(2)掌握平面向量的坐标运算;
(3)会根据向量的坐标,判断向量是否共线.
教学重点:平面向量的坐标运算
教学难点:向量的坐标表示的理解及运算的准确性
授课类型:新授课
教 具:多媒体、实物投影仪
教学过程:
3.已知:四点A(5, 1), B(3, 4), C(1, 3), D(5, -3) , 求证:四边形ABCD是梯形.
2.若A(0, 1), B(1, 2), C(3, 4) , 则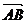 -2
-2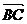 = .
= .
1.若M(3, -2) N(-5, -1) 且 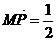
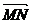 , 求P点的坐标
, 求P点的坐标
例1 已知A(x1,y1),B(x2,y2),求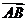 的坐标.
的坐标.
例2 已知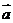 =(2,1),
=(2,1), 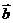 =(-3,4),求
=(-3,4),求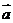 +
+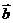 ,
,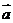 -
-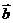 ,3
,3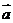 +4
+4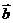 的坐标.
的坐标.
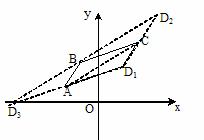
例3 已知平面上三点的坐标分别为A(-2, 1), B(-1, 3), C(3, 4),求点D的坐标使这四点构成平行四边形四个顶点.
解:当平行四边形为ABCD时,由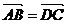 得D1=(2, 2)
得D1=(2, 2)
当平行四边形为ACDB时,得D2=(4, 6),当平行四边形为DACB时,得D3=(-6, 0)
例4已知三个力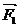 (3, 4),
(3, 4), 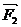 (2, -5),
(2, -5), 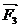 (x, y)的合力
(x, y)的合力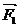 +
+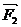 +
+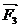 =
=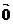 ,求
,求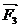 的坐标.
的坐标.
解:由题设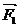 +
+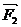 +
+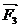 =
=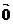 得:(3, 4)+ (2, -5)+(x, y)=(0, 0)
得:(3, 4)+ (2, -5)+(x, y)=(0, 0)
即: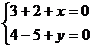 ∴
∴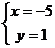 ∴
∴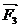 (-5,1)
(-5,1)
2.平面向量的坐标运算
(1)
若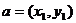 ,
,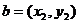 ,则
,则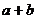
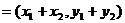 ,
,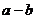
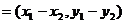
两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.
设基底为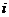 、
、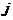 ,则
,则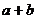
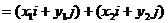
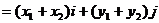
即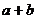
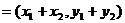 ,同理可得
,同理可得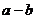
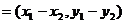
(2)
若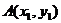 ,
,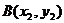 ,则
,则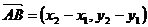
一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标.
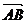 =
=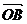 -
-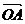 =( x2, y2)
- (x1,y1)= (x2- x1, y2- y1)
=( x2, y2)
- (x1,y1)= (x2- x1, y2- y1)
(3)若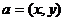 和实数
和实数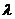 ,则
,则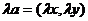 .
.
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标.
 设基底为
设基底为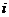 、
、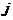 ,则
,则
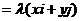
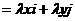 ,即
,即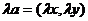
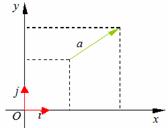
1.平面向量的坐标表示
如图,在直角坐标系内,我们分别取与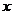 轴、
轴、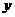 轴方向相同的两个单位向量
轴方向相同的两个单位向量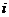 、
、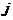 作为基底.任作一个向量
作为基底.任作一个向量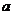 ,由平面向量基本定理知,有且只有一对实数
,由平面向量基本定理知,有且只有一对实数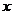 、
、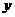 ,使得
,使得
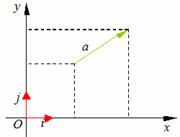
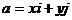 …………1
…………1
我们把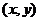 叫做向量
叫做向量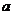 的(直角)坐标,记作
的(直角)坐标,记作
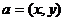 …………2
…………2
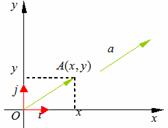 其中
其中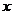 叫做
叫做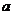 在
在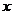 轴上的坐标,
轴上的坐标,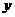 叫做
叫做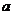 在
在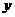 轴上的坐标,2式叫做向量的坐标表示.与
轴上的坐标,2式叫做向量的坐标表示.与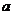 相等的向量的坐标也为
相等的向量的坐标也为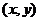 .
.
特别地,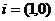 ,
,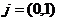 ,
,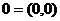 .
.
如图,在直角坐标平面内,以原点O为起点作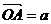 ,则点
,则点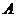 的位置由
的位置由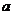 唯一确定.
唯一确定.
设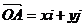 ,则向量
,则向量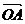 的坐标
的坐标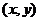 就是点
就是点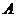 的坐标;反过来,点
的坐标;反过来,点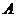 的坐标
的坐标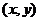 也就是向量
也就是向量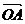 的坐标.因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示.
的坐标.因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com