
4.以平行六面体相邻两个面上互相异面的两条面对角线的端点为顶点的四面体的体积是平行六面体体积的( B )
?A.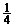 ? B.
? B. 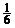 ? C.
? C.  ? D.
? D. 
3.正六棱柱ABCDEF-A1B1C1D1E1F1底面边长为1,侧棱长为 ,则这个棱柱的侧面对角线E1D与BC1所成的角是(
B ) A.90° B.60°? C.45° D.30°?
,则这个棱柱的侧面对角线E1D与BC1所成的角是(
B ) A.90° B.60°? C.45° D.30°?
2.设命题甲:“直四棱柱ABCD-A1B1C1D1中,平面ACB1与对角面BB1D1D垂直”;命题乙:“直四棱柱ABCD-A1B1C1D1是正方体”,那么,甲是乙的 ( C )
?A.充分必要条件 B.充分非必要条件 ?C.必要非充分条件 D.既非充分又非必要条件
1.具有下列性质的三棱锥中,哪一个是正棱锥 ( D )
?A.顶点在底面上的射影到底面各顶点的距离相等 ?B.底面是正三角形,且侧面都是等腰三角形
?C.相邻两条侧棱的夹角相等 ?D.三条侧棱相等,侧面与底面所成角也相等
4.在Rt△ABC中,∠C=30°,∠B=90°,D是BC边的中点,AC=2,DE⊥平面ABC,DE=1,则点E到斜边AC的
距离是 ( D )
A. ? B.
? B. ? C.
? C. ? D.
? D.
 典例剖析:
典例剖析:
例1.如图所示,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=a,D、E分别为棱AB、BC的中点,M为棱AA1上的点,二面角M-DE-A为30°.
(1)证明:A1B1⊥C1D; (2)求MA的长,并求点C到平面MDE的距离.
(1)证明 连结CD.∵三棱柱ABC-A1B1C1是直三棱柱,
∴CC1⊥平面ABC. ∴CD为C1D在平面ABC内的射影.
 ∵在△ABC中,AC=BC,D为AB的中点,
∵在△ABC中,AC=BC,D为AB的中点,
∴AB⊥CD,∴AB⊥C1D. ∵A1B1∥AB,∴A1B1⊥C1D.
(2)过点A作CE的平行线交ED的延长线于F,连结MF.
∵D、E分别为AB、BC的中点,∴DE∥AC. 又∵AF∥CE,CE⊥AC.∴AF⊥DE.
∵MA⊥平面ABC, ∴AF为MF在平面ABC内的射影,
∴MF⊥DE. ∴∠MFA为二面角M-DE-A的平面角,∠MFA=30°
在Rt△MAF中,AF= BC=
BC= ,∠MFA=30°,∴AM=
,∠MFA=30°,∴AM= a,
a,
作AG⊥MF于G. ∵MF⊥DE,AF⊥FE,∴DE⊥平面AMF. ∴平面MDE⊥平面AMF.∴AG⊥平面MDE.
在Rt△GAF中,∠GFA=30°,AF= . ∴AG=
. ∴AG= ,即点A到平面MDE的距离为
,即点A到平面MDE的距离为 .
.
∵CA∥DE,∴CA∥平面MDE, ∴点C到平面MDE的距离为 .
.
例2.已知正方形ABCD,边长为1,过D作PD⊥平面ABCD,且PD=1,E、F分别是AB、BC的中点.
(1)求D点到平面PEF的距离; (2)求直线AC到平面PEF的距离.
 解 (1)∵EF⊥BD,EF⊥PD. ∴EF⊥平面PDB.
解 (1)∵EF⊥BD,EF⊥PD. ∴EF⊥平面PDB.
∴平面PEF⊥平面PBD,交线为PG,∴D点到平面PEF的距离,就是D到PG的距离h.
在△PDG中,h= ,而PD=1,DG=
,而PD=1,DG= , PG=
, PG= ,
,
∴h=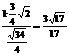 , 即D点到平面PEF的距离是
, 即D点到平面PEF的距离是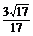 .
.
另解(等积法):
∵VD-PEF=VP-DEF,即 S△PEF·h=
S△PEF·h= S△DEF·PD, ∴h=
S△DEF·PD, ∴h=
∴D点到平面PEF的距离是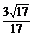 .
.
(2)连结AC交BD于O,则O到平面PEF的距离就为所求.因为平面PDG⊥平面PEF,所以O到PG
的距离就是O到平面PEF的距离.
 过O作OH⊥PG于H 在Rt△PDG中,∵OH⊥PG,
过O作OH⊥PG于H 在Rt△PDG中,∵OH⊥PG,
∴△PDG∽△OHG,∴ ∵PD=1,OG=
∵PD=1,OG=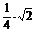 ,
,
∴PG= ∴OH=
∴OH=
∴直线AC到平面PEF的距离为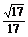 .
.
 例3.(07辽宁)如图,在直三棱柱
例3.(07辽宁)如图,在直三棱柱 中,
中, ,
, ,
,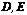 分别为棱
分别为棱 的中点,
的中点, 为棱
为棱 上的点,二面角
上的点,二面角 为
为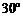 .(1)证明:
.(1)证明: (此小题略去不写);(2)求
(此小题略去不写);(2)求 的长,并求点
的长,并求点 到平面
到平面 的距离. (请用多种方法,至少要用向量法)
的距离. (请用多种方法,至少要用向量法)
(I)证明:连结 ,三棱柱
,三棱柱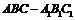 是直三棱柱,
是直三棱柱,

 平面
平面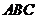 ,
,


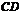 为
为 在平面
在平面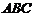 内的射影.
内的射影.
 中,
中, ,
, 为
为 中点,
中点,

 ,
, 
 .
.
 ,
,
 .
.
(II)解法一:过点 作
作 的平行线,交
的平行线,交 的延长线于
的延长线于 ,连结
,连结 .
.

 分别为
分别为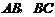 的中点,
的中点,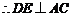 .
.
又
 ,
, .
.
 .
.
 平面
平面 ,
,

 为
为 在平面
在平面 内的射影.
内的射影.
 .
.
 为二面角
为二面角 的平面角,
的平面角, .
.
在 中,
中, ,
, ,
, .
.
作 ,垂足为
,垂足为 ,
, ,
, ,
,
 平面
平面 ,
, 平面
平面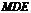
 平面
平面 ,
,

 平面
平面 .
.
在 中,
中, ,
,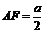 ,
,
 ,即
,即 到平面
到平面 的距离为
的距离为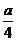 .
.

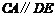 ,
,
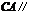 平面
平面 ,
,

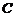 到平面
到平面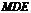 的距离与
的距离与 到平面
到平面 的距离相等,为
的距离相等,为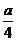 .
.
解法二:过点 作
作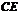 的平行线,交
的平行线,交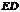 的延长线于
的延长线于 ,连接
,连接 .
.
 分别为
分别为 的中点,
的中点,

 .又
.又
 ,
,

 .
.
 平面
平面 ,
,

 是
是 在平面
在平面 内的射影,
内的射影,
 .
.

 为二面角
为二面角 的平面角,
的平面角,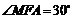 .
.
在 中,
中, ,
, ,
,
 .
.
设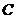 到平面
到平面 的距离为
的距离为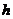 ,
,
 .
.
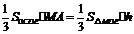
 ,
, ,
,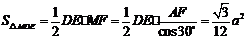 ,
,

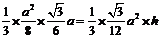 ,
,
 ,即
,即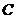 到平面
到平面 的距离为
的距离为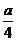 .
.
例4.如图,在直三棱柱ABC- 中,
中,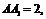 AB = 1,
AB = 1, ;点D、E分别在
;点D、E分别在 上,且
上,且 ,四棱锥
,四棱锥 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
 (1)求异面直线DE与
(1)求异面直线DE与 的距离;(2)若BC =
的距离;(2)若BC = ,求二面角
,求二面角 的平面角的正切值。
的平面角的正切值。
解法一:(Ⅰ)因 ,且
,且 ,故
,故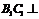 面
面 ,
,
从而 ,又
,又 ,故
,故 是异面直线
是异面直线 与
与 的公垂线.
的公垂线.
设 的长度为
的长度为 ,则四棱椎
,则四棱椎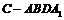 的体积
的体积 为
为
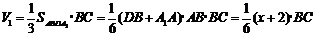 .
.
而直三棱柱 的体积
的体积 为
为 .
.
由已知条件 ,故
,故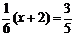 ,解之得
,解之得 .
.
从而 .
.
在直角三角形 中,
中, ,
,
又因 ,
, 故
故 .
.
(Ⅱ)如答(19)图1,过 作
作 ,垂足为
,垂足为 ,连接
,连接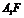 ,因
,因 ,
, ,故
,故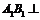 面
面 .
.
由三垂线定理知 ,故
,故 为所求二面角的平面角.
为所求二面角的平面角.
在直角 中,
中, ,
,
又因 ,
,
故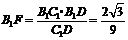 ,所以
,所以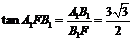 .
.
解法二:
(Ⅰ)如答(19)图2,以 点为坐标原点
点为坐标原点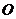 建立空间直角坐标系
建立空间直角坐标系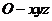 ,则
,则 ,
, ,
, ,
, ,则
,则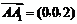 ,
, .设
.设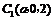 ,则
,则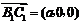 ,
,
 又设
又设 ,则
,则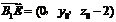 ,
,
从而 ,即
,即 .
.
又 ,所以
,所以 是异面直线
是异面直线 与
与 的公垂线.
的公垂线.
下面求点 的坐标.设
的坐标.设 ,则
,则 .
.
因四棱锥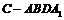 的体积
的体积 为
为

 .
.
而直三棱柱 的体积
的体积 为
为 .
.
由已知条件 ,故
,故 ,解得
,解得 ,即
,即 .
.
从而 ,
, ,
,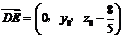 .
.
接下来再求点 的坐标.
的坐标.
由 ,有
,有 ,即
,即 (1)
(1)
又由 得
得 . (2)
. (2)
联立(1),(2),解得 ,
, ,即
,即 ,得
,得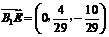 .故
.故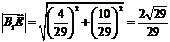 .
.
(Ⅱ)由已知 ,则
,则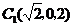 ,从而
,从而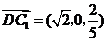 ,过
,过 作
作 ,
,
垂足为 ,连接
,连接 ,设
,设 ,则
,则 ,因为
,因为 ,故
,故
 ……………………………………①
……………………………………①
因 且
且 得
得 ,即
,即
 ……………………………………②
……………………………………②
联立①②解得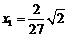 ,
, ,即
,即 .
.
则 ,
, .
. .
.
又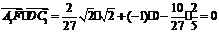 ,故
,故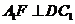 ,
,
因此 为所求二面角的平面角.又
为所求二面角的平面角.又 ,从而
,从而 ,
,
故
 ,
, 为直角三角形,所以
为直角三角形,所以 .
.
3.一副三角板如图拼接,使两个三角板所在的平面互相垂直.如果公共边AC=a,
则异面直线AB与CD的距离是( C )?
A. B.a? C.
B.a? C. D.
D.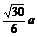
1.在△ABC中,AB=AC=5,BC=6,PA⊥平面ABC,PA=8,则P到BC的距离为 ( D )
 ?A.
?A. ? B.2
? B.2 ? C.3
? C.3 ? D.4
? D.4
7.求距离的一般步骤:①找出或作出相关的距离;②证明它符合定义;③归到某三角形或多边形中计算;④作答.
课前练习:
6.距离的共性:这其中距离中,虽然定义不同,但总具有下列几个特征:
①指相应线段的长度;②相关线段中最短的;③除两点间距离外,其余总与垂直相联系,方法就有几何法和代数等方法.
5.直线到平面的距离:一条直线上的任一点到与它平行的平面的距离,叫做这条直线到平面的距离(转化为点面距离).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com