
2.共面向量定理:两个向量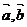 不共线,则向量
不共线,则向量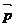 与向量
与向量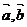 共面的充要条件是存在实数对x,y使
共面的充要条件是存在实数对x,y使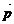 =
=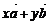 .
.
推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y使得: ,或对空间任意一点O有:
,或对空间任意一点O有: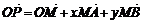 .
.
1.共线向量:对空间任意两个向量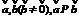 <=>存在唯一实数l使
<=>存在唯一实数l使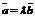 .
.
若直线过点A、B,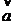 是方向向量,则点P在直线
是方向向量,则点P在直线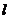 上
上
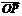 =(1-t)
=(1-t)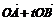 (
(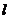 的向量方程)
的向量方程)
3.若a=(2x,1,3),b=(1,-2y,9),且a∥b,则 ( )
?A.x=1,y=1? B.x=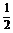 ,y=-
,y=-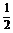 ?C.x=
?C.x=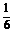 ,y=-
,y=-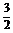 D.x=-
D.x=-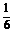 ,y=
,y=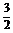
例1已知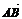 =(2,2,1),
=(2,2,1), =(4,5,3),求平面ABC的单位法向量.
=(4,5,3),求平面ABC的单位法向量.
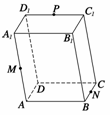 例2 如图所示,在平行六面体ABCD-A1B1C1D1中,设
例2 如图所示,在平行六面体ABCD-A1B1C1D1中,设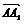 =a,
=a,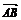 =b,
=b,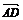 =c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:(1)
=c,M,N,P分别是AA1,BC,C1D1的中点,试用a,b,c表示以下各向量:(1)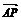 ;(2)
;(2)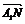 ;(3)
;(3)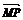 +
+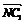 .
.
例3 已知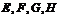 分别是空间四边形ABCD的边
分别是空间四边形ABCD的边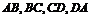 的中点,(1)求证:
的中点,(1)求证: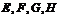 四点共面;
四点共面;
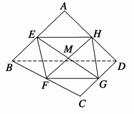 (2)求证:BD∥平面EFGH;(3)设M是EG和FH的交点,求证:对空间任一点O,有
(2)求证:BD∥平面EFGH;(3)设M是EG和FH的交点,求证:对空间任一点O,有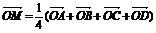 .
.
例4 (1)求与向量a=(2,-1,2)共线且满足方程a·x=-18的向量x的坐标;
(2)已知A、B、C三点坐标分别为(2,-1,2)、(4,5,-1)、(-2,2,3),求点P的坐标使得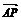 =
=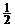 (
(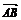 -
-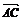 );
);
(3)已知a=(3,5,-4),b=(2,1,8),求: ①a·b;②a与b夹角的余弦值;③确定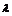 ,
,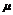 的值使得
的值使得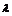 a+
a+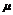 b与z轴垂直,且(
b与z轴垂直,且(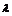 a+
a+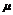 b)·(a+b)=53.
b)·(a+b)=53.
2.下列命题中是真命题的是 ( ) A.分别表示空间向量的有向线段所在的直线是异面直线,则这两个向量不是共面向量
?B.若|a|=|b|,则a,b的长度相等而方向相同或相反 C.若向量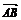 ,
,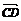 满足|
满足|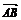 |>|
|>|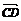 |,且
|,且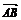 与
与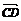 同向,则
同向,则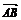 >
>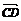 ?D.若两个非零向量
?D.若两个非零向量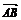 与
与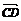 满足
满足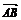 +
+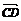 =0,则
=0,则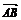 ∥
∥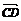
1.有4个命题:①若p=xa+yb,则p与a、b共面; ②若p与a、b共面,则p=xa+yb; ③若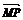 =x
=x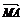 +y
+y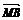 ,则P、M、A、B共面; ④若P、M、A、B共面,则
,则P、M、A、B共面; ④若P、M、A、B共面,则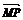 =x
=x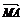 +y
+y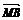 . 其中真命题的个数是 (
)
. 其中真命题的个数是 (
)
?A.1? B.2? C.3? D.4
7.若表示向量a1,a2,…,an的有向线段终点和始点连结起来构成一个封闭折图形,则
基础自测
6. 模长公式: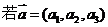 ,
,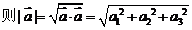
5.空间向量的直角坐标运算律: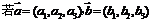
则 ;
;

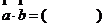 ,
, 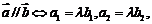
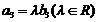 ,
,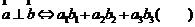 .
.
4.向量的数量积: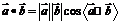 ,
,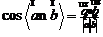 ,;
,;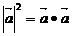 ,
,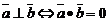 ,
,
3.空间向量基本定理:若向量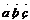 不共面,则对空间任意一向量
不共面,则对空间任意一向量 ,存在惟一有序实数对x、y、z使得
,存在惟一有序实数对x、y、z使得
推论:设O、A、B、C是不共面的四点,则对空间任意一点P,都存在惟一的三个有序实数x、y、z使 。特别地,当 时,则必有P、A、B、C四点共面.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com