
30.已知直线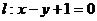 ,⊙
,⊙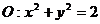 上的任意一点P到直线
上的任意一点P到直线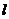 的距离为
的距离为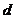 。当
。当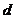 取得最大时对应P的坐标
取得最大时对应P的坐标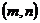 ,设
,设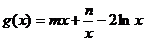 。
。
(1)
 求证:当
求证:当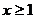 ,
,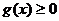 恒成立;
恒成立;
(2)
 讨论关于
讨论关于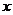 的方程:
的方程: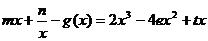 根的个数。
根的个数。
29.已知圆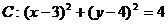 ,直线
,直线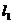 过定点
过定点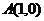 。
。
(1)若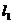 与圆相切,求
与圆相切,求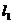 的方程;
的方程;
(2)若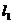 与圆相交于
与圆相交于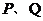 丙点,线段
丙点,线段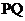 的中点为
的中点为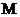 ,又
,又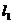 与
与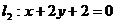 的交点为
的交点为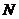 ,判断
,判断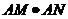 是否为定值,若是,则求出定值;若不是,请说明理由。
是否为定值,若是,则求出定值;若不是,请说明理由。
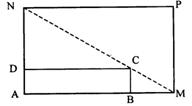
28.如图所示,将一矩形花坛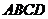 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园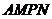 ,要求B在
,要求B在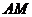 上,D在
上,D在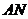 上,且对角线
上,且对角线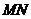 过C点,已知AB=3米,AD=2米,
过C点,已知AB=3米,AD=2米,
 (1)要使矩形
(1)要使矩形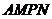 的面积大于32平方米,则
的面积大于32平方米,则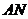 的长应在什么范围内?
的长应在什么范围内?
(2)当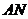 的长度是多少时,矩形
的长度是多少时,矩形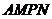 的面积最小?并求最小面积;
的面积最小?并求最小面积;
(3)若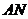 的长度不少于6米,则当
的长度不少于6米,则当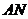 的长度是多少时,矩形
的长度是多少时,矩形 的面积最小?并求出最小面积。
的面积最小?并求出最小面积。
27.多面体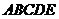 中,
中,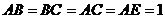 ,
,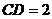 ,
,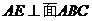 ,
,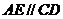 。
。
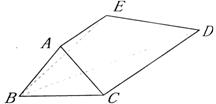 (1)求证:
(1)求证: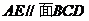 ;
;
(2)求证: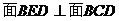 。
。
26.已知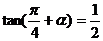
(1)求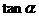 的值;
的值;
(2)求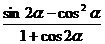 的值。
的值。
25.给出下列四个结论:
①若A、B、C、D是平面内四点,则必有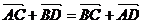 ;
;
②“a>b>0”是“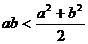 ”的充要条件;
”的充要条件;
③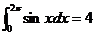 ;
;
④已知点 图象的一个对称中心和一条对称轴,则
图象的一个对称中心和一条对称轴,则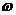 的最小值为2;
的最小值为2;
其中正确结论的序号是 。(填上所有正确结论的序号)
23.一船向正北匀速行驶,看见正西方两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度是 海里/小时。
 24.已知
24.已知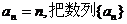 的各项排列成如下的三角形状:
的各项排列成如下的三角形状:
记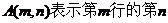 个数,
个数,
则A(21,12)= 。
22.已知圆锥的底面半径为1,高为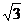 ,则圆锥的表面积为
。
,则圆锥的表面积为
。
21.已知0<x<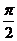 ,t是大于零的常数,且函数
,t是大于零的常数,且函数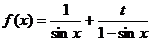 的最小值为9,则t的值为
。
的最小值为9,则t的值为
。
20. 已知函数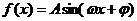 (
(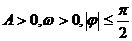 )是定义域为R的奇函数,且当
)是定义域为R的奇函数,且当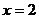 时,
时,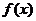 的图象在
的图象在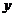 轴右侧取得第一个最大值为2,则
轴右侧取得第一个最大值为2,则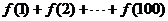 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com