
1.1已知函数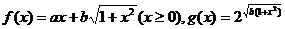 ,且
,且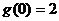 ,
,
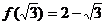 .
.
(Ⅰ)求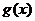 的值域
的值域
(Ⅱ)指出函数 的单调性(不需证明),并求解关于实数
的单调性(不需证明),并求解关于实数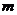 的不等式
的不等式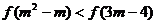 ;
;
(Ⅲ)定义在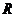 上的函数
上的函数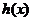 满足
满足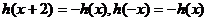 ,且当
,且当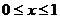 时
时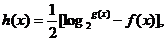 求方程
求方程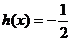 在区间
在区间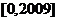 上的解的个数.
上的解的个数.
1. 1.1
1.1
东
61东北师大附中
5.雅礼中学2010届高三月考卷(四)
设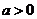 ,函数
,函数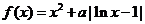
(1)当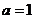 时,求曲线
时,求曲线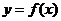 在
在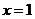 处的切线方程;
处的切线方程;
(2)当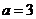 时,求函数
时,求函数 的单调性;
的单调性;
(3)当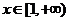 时,求函数
时,求函数 的最小值。
的最小值。



4.(湖南省四市九校2010届高三第一次联考试题)已知数列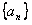 的相邻两项
的相邻两项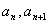 是关于
是关于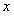 的方程
的方程
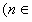 N
N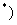 的两根,且
的两根,且 .
.
(I)求证: 数列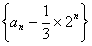 是等比数列;w.w.^w.k.s.5*(II)设
是等比数列;w.w.^w.k.s.5*(II)设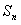 是数列
是数列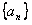 的前
的前 项和,求
项和,求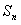 .
.
(III)问是否存在常数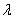 ,使得
,使得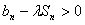 对任意
对任意 N
N 都成立,若存在,
都成立,若存在,
求出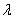 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由. 即
即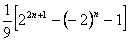
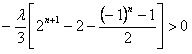 (*)对任意
(*)对任意 N
N 都成立
都成立

1.解:(1)由必要条件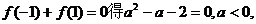
所以a=-1, 下面 证充分性,当a=-1时,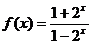 ,
,
任取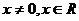 ,
,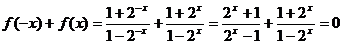 恒成立, 由A={-1}。 (2)法一,当a=-1时,由
恒成立, 由A={-1}。 (2)法一,当a=-1时,由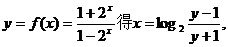
互换x,y得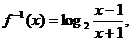 则
则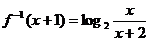 ,
,
从而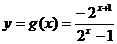 所以
所以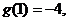 即B={-4}
即B={-4}
法二、当a=-1时,由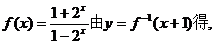

互换x,y得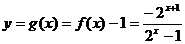 …………8分
…………8分
所以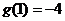 即B={-4} (3)原问题转化为
即B={-4} (3)原问题转化为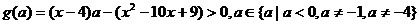
恒成立,则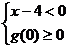 或
或 则x的取值范围为[,4]。
则x的取值范围为[,4]。
2解:(1)因为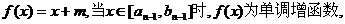
所以其值域为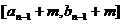 …………2分
…………2分
于是 …………4分
…………4分
又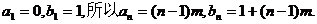 …………6分
…………6分
(2)因为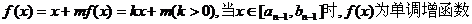
所以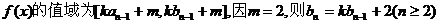 ……8分
……8分
法一:假设存在常数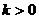 ,使得数列
,使得数列 ,得
,得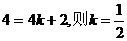 符合。 …………12分
符合。 …………12分
法二:假设存在常数k>0,使得数列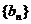 满足
满足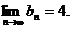
当k=1不符合。……9分
当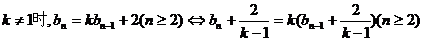 ,
,
则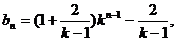 …………11分
…………11分
当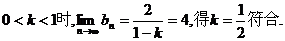 …………12分
…………12分
(3)因为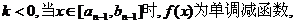
所以 的值域为
的值域为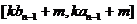 …………13分
…………13分
于是 …………14分
…………14分
则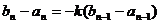 又
又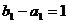
则有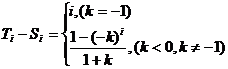 …………16分
…………16分
进而有
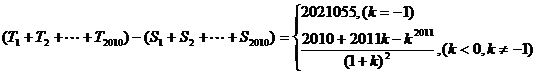
2. 已知函数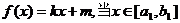 时,
时, 的值域为
的值域为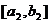 ,当
,当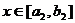
时, 的值域为
的值域为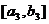 ,依次类推,一般地,当
,依次类推,一般地,当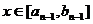 时,
时, 的值域为
的值域为
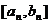 ,其中k、m为常数,且
,其中k、m为常数,且
(1)若k=1,求数列 的通项公式;
的通项公式;
(2)项m=2,问是否存在常数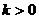 ,使得数列
,使得数列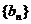 满足
满足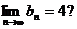 若存在,求k的值;若不存在,请说明理由;
若存在,求k的值;若不存在,请说明理由;
(3)若 ,设数列
,设数列 的前n项和分别为Sn,Tn,求
的前n项和分别为Sn,Tn,求
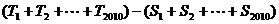 。
。
3.(上海市十三校2010届高三第一次联考)
1已知函数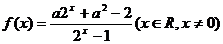 ,其中a为常数,且
,其中a为常数,且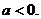
(1)若 是奇函数,求a的取值集合A;
是奇函数,求a的取值集合A;
(2)当a=-1时,设 的反函数为
的反函数为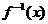 ,且函数
,且函数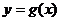 的图像与
的图像与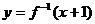 的图像关于
的图像关于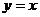 对称,求
对称,求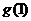 的取值集合B。
的取值集合B。
(3)对于问题(1)(2)中的A、B,当 时,不等式
时,不等式
 恒成立,求x的取值范围。
恒成立,求x的取值范围。
1.解:(1)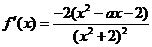 ……………………………………………1分
……………………………………………1分
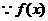 在
在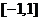 上是增函数
上是增函数
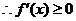 即
即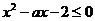 ,在
,在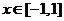 恒成立 …………① …………3分
恒成立 …………① …………3分
设 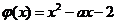 ,则由①得
,则由①得
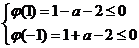 解得
解得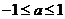
所以,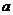 的取值范围为
的取值范围为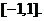 ………………………………………………………6分
………………………………………………………6分
(2)由(1)可知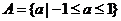
由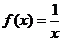 即
即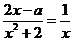 得
得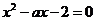

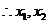 是方程
是方程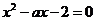 的两个非零实根
的两个非零实根
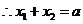 ,
, ,又由
,又由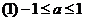
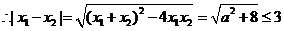 ……………………………9分
……………………………9分
于是要使 对
对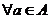 及
及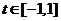 恒成立
恒成立
即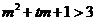 即
即 对
对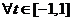 恒成立 ………②………11分
恒成立 ………②………11分
 设
设 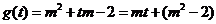 ,则由②得
,则由②得
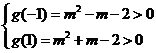 解得
解得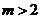 或
或
故存在实数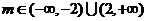 满足题设条件…………………………14分
满足题设条件…………………………14分
2解:(1)由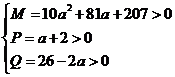 得
得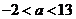 ……………2分
……………2分
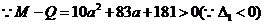 ………………………3分
………………………3分
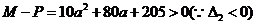 ………………………4分
………………………4分
 ,
,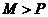
又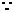 当
当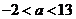 时,
时,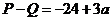 ,
,
当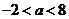 时,即
时,即 ,则
,则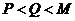 ………………………5分
………………………5分
当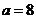 时,
时,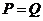 ,则
,则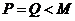
当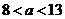 时,
时,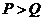 ,则
,则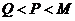
(2)依题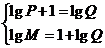 即
即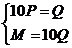
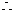
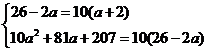
解得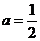 ,从而
,从而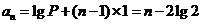 ………………………9分
………………………9分
(3) ,设
,设 与
与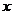 轴交点为
轴交点为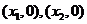
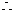 当
当 =0时有
=0时有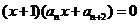
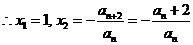 ………………………………………11分
………………………………………11分

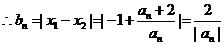
又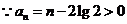 ,
,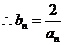
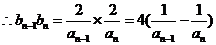
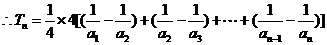
 …………14分
…………14分
2. 设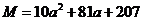 ,
,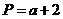 ,Q=
,Q=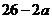 ;若将
;若将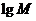 ,
,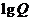 ,
,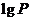 适当排序后可构成公差为1的等差数列
适当排序后可构成公差为1的等差数列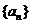 的前三项
的前三项
 (I)在使得
(I)在使得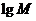 ,
,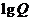 ,
,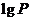 有意义的条件下,试比较
有意义的条件下,试比较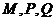 的大小;
的大小;
(II)求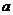 的值及数列
的值及数列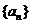 的通项;
的通项;
(III)记函数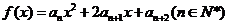 的图象在
的图象在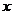 轴上截得的线段长为
轴上截得的线段长为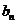 ,设
,设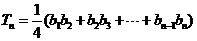 ,求
,求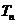 .
.
1.已知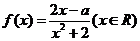 在区间
在区间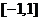 上是增函数
上是增函数
(I)求实数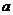 的取值范围;
的取值范围;
(II)记实数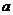 的取值范围为集合A,且设关于
的取值范围为集合A,且设关于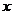 的方程
的方程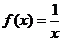 的两个非零实根为
的两个非零实根为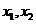 。
。
①求 的最大值;
的最大值;
②试问:是否存在实数m,使得不等式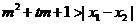 对
对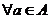 及
及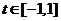 恒成立?若存在,求m的取值范围;若不存在,请说明理由.
恒成立?若存在,求m的取值范围;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com