
9.
一颗正方体骰子,其六个面上的点数分别为1,2,3,4,5,6,将这颗骰子抛掷三次,观察向上的点数,则三次点数之和等于16的概率为_________.
8.
在△ABC中,AB=2,AC=1,D为BC的中点,则 =_________.
=_________.
7.
已知 是两条不同的直线,
是两条不同的直线, 为两个不同的平面,
为两个不同的平面,
有下列四个命题:
①若 ,m⊥n,则
,m⊥n,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则 ;
;
④若 ,则
,则 .
.
其中正确的命题是(填上所有正确命题的序号)_______________.①④
6.
椭圆 的一条准线方程为
的一条准线方程为 ,则
,则 ________.5
________.5
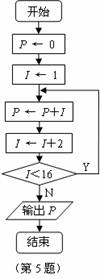
5. 如图,程序执行后输出的结果为_________.64.
4.
函数 的值域是_________.(0,+∞)
的值域是_________.(0,+∞)
3. 直线x+ay+3=0与直线ax+4y+6=0平行的充要条件是_________.
 a=-2.
a=-2.
2.
已知复数 ,
, (
( 是虚数单位),若
是虚数单位),若 为纯虚数,则实数
为纯虚数,则实数 =_________.
=_________.
1.
集合 的所有子集个数为_________.8
的所有子集个数为_________.8
|
15(本题满分14分) (1)  , ,    (定值) (定值)(2)由(1)可知A、B为锐角  所以  的最大值为 的最大值为 ,此时三角形ABC为钝角三角形。 ,此时三角形ABC为钝角三角形。 |
16⑴证明:连结 ,则 ,则 // // , ∵ , ∵ 是正方形,∴ 是正方形,∴ . .∵  面 面 ,∴ ,∴ . .又  ,∴ ,∴ 面 面 . . 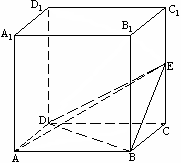 ∵ ∵ 面 面 ,∴ ,∴ , ,∴  . .
⑵证明:作  的中点F,连结 的中点F,连结 . .∵  是 是 的中点,∴ 的中点,∴   , ,∴四边形  是平行四边形,∴ 是平行四边形,∴  . . ∵  是 是 的中点,∴ 的中点,∴ , ,又  ,∴ ,∴ . .∴四边形  是平行四边形, 是平行四边形, // // , ,∵  , , , ,∴平面  面 面 . . 又  平面 平面 ,∴ ,∴ 面 面 . . |
|
17(本题满分14分) (1)  恒成立 恒成立 (2)  “p或q”为真命题且“p且q”为假命题,即p,q一真一假 故  |
18(1)由 ,得 ,得 若函数为  上单调增函数,则 上单调增函数,则 在 在 上恒成立, 上恒成立,即不等式  在 在 上恒成立. 也即 上恒成立. 也即 在 在 上恒成立. 上恒成立. 令  ,上述问题等价于 ,上述问题等价于 ,而 ,而 为在 为在 上的减函数,则 上的减函数,则 ,于是 ,于是 为所求. 为所求.
(2)证明:由  得 得  … … 而
而 ①
又 ①
又 , ∴ , ∴ ② ②∵  ∴ ∴ , ,∵  ∴ ∴ ③ ③ 由①、②、③得  即  ,从而由凹函数的定义可知函数为凹函数 ,从而由凹函数的定义可知函数为凹函数 |
|
19(本题满分16分) (1)证明:直线  恒过(1,1)又点在园内,所以直线和圆恒有两个公共点; 恒过(1,1)又点在园内,所以直线和圆恒有两个公共点;(2)设  则 则  轨迹是半径为 轨迹是半径为 的圆。 的圆。(3)设  , , 由直线与圆方程联立得 由直线与圆方程联立得 解得 解得 ,所求直线方程为 ,所求直线方程为 |
|
20(本题满分16分) (1)  在[0,1]上为增函数, 在[0,1]上为增函数, (2)   两式相减得: 两式相减得: 递推一次 递推一次  所以  (3)  , , 且 且 也满足 也满足存在  使得 使得 对所有的 对所有的 成立。 成立。 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com