
20、(本小题满分16分)
已知函数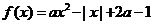 (
(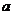 为实常数).
为实常数).
(1)若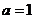 ,求
,求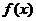 的单调区间;
的单调区间;
(2)若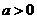 ,设
,设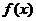 在区间
在区间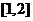 的最小值为
的最小值为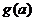 ,求
,求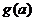 的表达式;
的表达式;
(3)设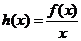 ,若函数
,若函数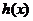 在区间
在区间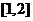 上是增函数,求实数
上是增函数,求实数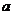 的取值范围.
的取值范围.
19、(本小题满分16分)
在平面直角坐标系中,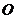 为坐标原点,已知
为坐标原点,已知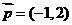 ,
,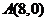 ,
,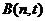 ,
,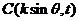 ,其中
,其中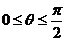
(1)若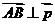 ,且
,且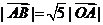 ,求向量
,求向量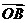 ;
;
(2)若向量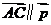 ,当
,当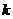 为大于4的某个常数时,
为大于4的某个常数时,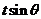 取最大值4,求此时
取最大值4,求此时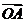 与
与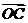 夹角的正切值.
夹角的正切值.
18、(本小题满分16分)
 某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
|
|
年固定成本 |
每件产品成本 |
每件产品销售价 |
每年最多可生产的件数 |
|
A产品 |
20 |
m |
10 |
200 |
|
B产品 |
40 |
8 |
18 |
120 |
其中年固定成本与年生产的件数无关,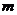 是待定常数,其值由生产
是待定常数,其值由生产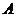 产品的原材料决定,预计
产品的原材料决定,预计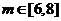 ,另外,年销售
,另外,年销售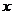 件B产品时需上交
件B产品时需上交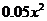 万美元的特别关税,假设生产出来的产品都能在当年销售出去.
万美元的特别关税,假设生产出来的产品都能在当年销售出去.
(1)求该厂分别投资生产A、B两种产品的年利润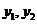 与生产相应产品的件数
与生产相应产品的件数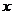 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;
(2)如何投资才可获得最大年利润?请设计相关方案.
17、(本小题满分14分)
设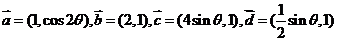 其中
其中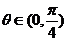 .
.
(1)求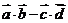 的取值范围;
的取值范围;
(2)若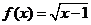 ,
,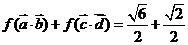 ,求
,求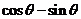 的值.
的值.
16、(本小题满分14分)
已知函数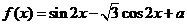
(1)求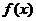 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)当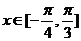 时,函数
时,函数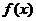 的最大值与最小值的和
的最大值与最小值的和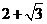 ,求
,求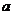 .
.
15、(本小题满分14分)
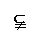 已知函数
已知函数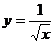 的定义域为集合A,集合
的定义域为集合A,集合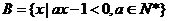 ,集合C =
,集合C =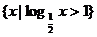 ,且
,且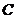 (A∩B).
(A∩B).
(1)求A∩C;(2)求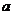 .
.
14、几位同学在研究函数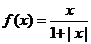
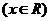 时,给出了下面几个结论:
时,给出了下面几个结论:
①函数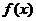 的值域为
的值域为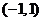 ;②若
;②若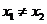 ,则一定有
,则一定有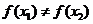 ;③
;③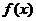 在
在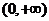 是增函数;④若规定
是增函数;④若规定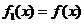 ,
,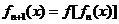 ,则
,则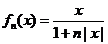 对任意
对任意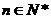 恒成立,上述结论中正确的个数有____▲____个.
恒成立,上述结论中正确的个数有____▲____个.
13、若函数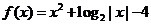 的零点
的零点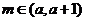 ,
,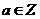 ,则所有满足条件的
,则所有满足条件的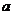 的和为______▲_______.
的和为______▲_______.
12、半圆的直径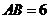 ,
,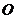 为圆心,
为圆心,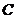 为半圆上不同于
为半圆上不同于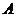 、
、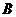 的任意一点,若点
的任意一点,若点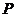 为半径
为半径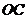 上的动点,则
上的动点,则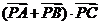 的最小值为______▲_______.
的最小值为______▲_______.
11、设定义在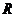 上的函数
上的函数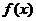 同时满足以下三个条件:①
同时满足以下三个条件:①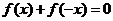 ②
②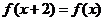 ③当
③当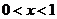 时,
时,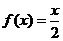 ,则
,则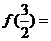 ______▲_______.
______▲_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com