
即先放低的调子,抑制住某人或事物,然后再升高格调,呈现给读者一种曲折的美,使主题更加鲜明。
[例]曾经以为,古代文人的生命会简单而明了,时代赋予他们简明的期望:入相出将,封妻荫子。然而,是谁?偏偏要抛开那些世俗的期望,独上高楼,为自己的人生另择一条路?(2004年重庆高考优秀作文《独上高楼》)
--“简单而明了”--“偏偏要”,说明生命并不简单,点明他人期望与自我认识的矛盾,引出论题。
[例]白居易在《琵琶行》中写下了“别有幽愁暗恨生,此时无声胜有声”的千古绝句。也许,这是当时千言万语在无言中的最好写照。但有时,或者说更多的时候应是有声胜无声。(引自广东2004年高考优秀卷《此时有声胜无声》)
--“无声胜有声”--“有声胜无声”点明中心论点。
3.其它自然现象或事物类比起兴法。
[例]
泉水激石,泠泠作响;好鸟相鸣,嘤嘤成韵。这是和谐的自然美。
层台耸翠,上出重霄;飞阁流丹,下临无地。这是和谐的艺术美。
政通人和,百业俱兴;国富民强,万民同乐。这是和谐的社会美。
和谐即美,美即和谐。
和谐的社会之美,必须你我共同创造。(编者下水文章《你我共创和谐之美》)
--对偶+引诗写物+议论,引出论题。
2.植物类比起兴法。
小草是平凡的,但它默默地绽绿吐翠,它是自豪的,因为有了它,大地才充满生机;石子是平凡的,但它甘愿充当铺路石,它是自豪的,因为有了它,人们才有了道路;农民是平凡的,但他们默默耕耘,他们是自豪的,因为有了他们,社会才有了具大的物质财富……(2004年辽宁高考优秀作文《我平凡,我自豪》)
--拟人写植物+大致排比,由物及人,段末照应题目,即照应中心论点。
1.动物类比起兴法。
起兴:先言他物以引起所言之物。可以起类比作用;还可以奠定情感气氛。写时要注意简短,点到就行,不要过长,以致入题太慢,影响下文的论述。
[例]虎啸深林,震慑百兽,这是强势语言的威力;鹦鹉学舌,招杀身祸,这是弱势语言的悲剧。短短三寸之舌,可骂死周瑜,可退秦师,堪谓有千斤之重也。(2004年广东高考优秀卷《千斤之舌》)--(续写、议论)+(对比+比喻+借代+夸张)。
[说明]要说“语言”,先说鸟兽,把鸟兽的叫声喻为“语言”,对比叫声强弱的不同作用,以此类比语言的重要作用,照应题目,暗含中心论点,说理形象生动。
[例]种子冲破岩层的禁锢;迎向光明;雄鹰冲破风暴的阻遏,飞向云霄;骏马突破缰绳的束缚,奔向原野;海燕突破雷电的肆虐,迎来自由。
《自由》--排比+托物起兴,照应题目,引出论题。
21.(本小题满分14分)已知函数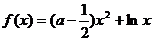 (
(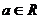 )。
)。
(Ⅰ)当 时,求
时,求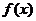 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数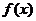 的图象恒在直线
的图象恒在直线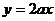 下方,求
下方,求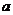 的取值范围。
的取值范围。
|
广东省 |
广州市广东番禺仲元中学 中山市第一中学 深圳市宝安中学 |
六校 联合体 |
|
汕头市潮阳第一中学 佛山市南海中学 揭阳市普宁第二中学 |
20.(本小题满分14分)如图所示的几何体 中,
中,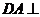 平面
平面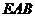 ,
,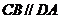 ,
,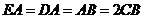 ,
,
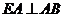 ,
,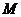 是
是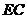 的中点。
的中点。
(Ⅰ)求证: ;
;
(Ⅱ)设二面角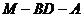 的平面角为
的平面角为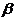 ,求
,求 。
。
19.(本小题满分14分)已知点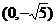 是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为
是中心在原点,长轴在x轴上的椭圆的一个顶点,离心率为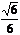 ,椭圆的左右焦点分别为F1和F2 。
,椭圆的左右焦点分别为F1和F2 。
(Ⅰ)求椭圆方程;
(Ⅱ)点M在椭圆上,求⊿MF1F2面积的最大值;
(Ⅲ)试探究椭圆上是否存在一点P,使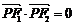 ,若存在,请求出点P的坐标;若不存在,请说明理由。
,若存在,请求出点P的坐标;若不存在,请说明理由。

18.(本小题满分14分)甲、乙等五名亚运志愿者被随机地分到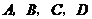 四个不同的赛场服务,每个赛场至少有一名志愿者 。
四个不同的赛场服务,每个赛场至少有一名志愿者 。
(Ⅰ)求甲、乙两人同时参加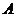 赛场服务的概率;
赛场服务的概率;
(Ⅱ)求甲、乙两人不在同一个赛场服务的概率;
(Ⅲ)设随机变量 为这五名志愿者中参加
为这五名志愿者中参加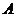 赛场服务的人数,求
赛场服务的人数,求 的分布列。
的分布列。
17.(本小题满分12分)在数列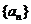 中,
中, ,
,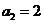 ,且
,且 (
( )。
)。
(Ⅰ)设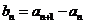 (
(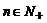 ),求数列
),求数列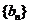 的通项公式;
的通项公式;
(Ⅱ)求数列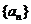 的通项公式 。
的通项公式 。
16.(本小题满分12分)设函数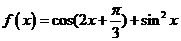 。
。
(Ⅰ)求函数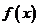 的最小正周期,并判断奇偶性;
的最小正周期,并判断奇偶性; 

(Ⅱ)设A,B,C为 的三个内角,若
的三个内角,若 ,且C为锐角,求
,且C为锐角,求 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com