
(四)艺术手法
(三)词中塑造了怎样的一个形象?
(二)根据你的理解,分析下面的几句话,你认为在词中有什么深刻含义?
1、竹杖芒鞋轻胜马,谁怕!一蓑烟雨任平生。
2、“料峭春风吹酒醒。微冷。山头斜照却相迎”三句,给我们以怎样的人生启示?
3、回首向来萧洒处,归去,也无风雨也无晴。
(一)重点字词
1、 词中“莫听”、“何妨”两个词语,表达了作者怎样的情怀?
2、“竹杖芒鞋轻胜马”中的“轻”字有何含义?
词的内容(上阙、下阙)
上阙主要写的内容
下阙主要写的内容
此词作于宋神宗元丰五年,词人贬谪黄州后的第三年。
苏轼(1037-1101年),字 ,号 ,谥号 。北宋眉
州眉山(即今四川眉山)人,是宋代(北宋)著名的文学家、书画家。他与他的父亲 、弟弟 皆以文学名世,世称“三苏”。且苏轼与唐代的 、 和宋代的 、 、 、 、合称“唐宋八大家”。并与 、 、 被称为最能代表宋代书法成就的书法家,合称为"宋四家"。苏氏四门生为: 、 、 、 。
嘉佑元年(1056年),二十岁的考中进士。神宗即位后,任用王安石支持变法。苏轼上书反对,自求外放,调任杭州通判,后又被调往密州、徐州、湖州等地。后发生“乌台诗案”,差点被杀。被贬为黄州团练副使。
哲宗即位后,又不能容于旧党,因而再度自求外调。他以龙图阁学士的身分,再次到阔别了十六年的杭州当太守。苏轼在杭州修了一项重大的水利工程,也就是著名的“苏堤”。
元佑八年(1093年)新党再度执政,八年后回京,北归途中,卒于常州。
8、函数的最大值和最小值:
(1)定义:函数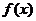 在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数
在一闭区间上的最大值是此函数在此区间上的极大值与其端点值中的“最大值”;函数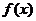 在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。
在一闭区间上的最小值是此函数在此区间上的极小值与其端点值中的“最小值”。
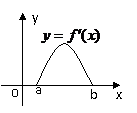 (2)求函数
(2)求函数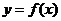 在[
在[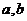 ]上的最大值与最小值的步骤:(1)求函数
]上的最大值与最小值的步骤:(1)求函数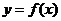 在(
在(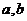 )内的极值(极大值或极小值);(2)将
)内的极值(极大值或极小值);(2)将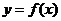 的各极值与
的各极值与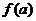 ,
,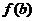 比较,其中最大的一个为最大值,最小的一个为最小值。如(1)函数
比较,其中最大的一个为最大值,最小的一个为最小值。如(1)函数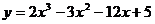 在[0,3]上的最大值、最小值分别是______(答:5;
在[0,3]上的最大值、最小值分别是______(答:5;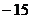 );(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为
);(2)用总长14.8m的钢条制作一个长方体容器的框架,如果所制作容器的底面的一边比另一边长0.5m。那么高为多少时容器的容积最大?并求出它的最大容积。(答:高为1.2米时,容积最大为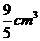 )
)
特别注意:(1)利用导数研究函数的单调性与最值(极值)时,要注意列表!(2)要善于应用函数的导数,考察函数单调性、最值(极值),研究函数的性态,数形结合解决方程不等式等相关问题。如(1)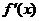 是
是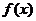 的导函数,
的导函数,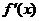 的图象如右图所示,则
的图象如右图所示,则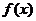 的图象只可能是
( 答:D )
的图象只可能是
( 答:D )
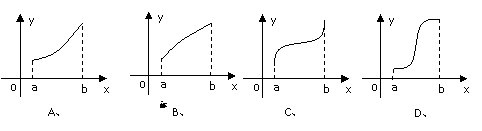
(2)方程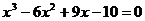 的实根的个数为______(答:1);(3)已知函数
的实根的个数为______(答:1);(3)已知函数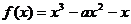 ,抛物线
,抛物线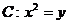 ,当
,当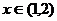 时,函数
时,函数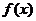 的图象在抛物线
的图象在抛物线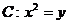 的上方,求
的上方,求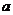 的取值范围(答:
的取值范围(答: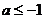 )。
)。
7、函数的极值:
(1)定义:设函数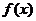 在点
在点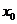 附近有定义,如果对
附近有定义,如果对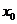 附近所有的点,都有
附近所有的点,都有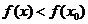 ,就说是
,就说是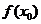 函数
函数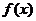 的一个极大值。记作
的一个极大值。记作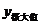 =
=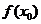 ,如果对
,如果对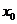 附近所有的点,都有
附近所有的点,都有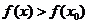 ,就说是
,就说是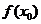 函数
函数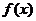 的一个极小值。记作
的一个极小值。记作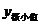 =
=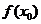 。极大值和极小值统称为极值。
。极大值和极小值统称为极值。
(2)求函数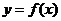 在某个区间上的极值的步骤:(i)求导数
在某个区间上的极值的步骤:(i)求导数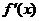 ;(ii)求方程
;(ii)求方程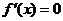 的根
的根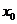 ;(iii)检查
;(iii)检查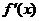 在方程
在方程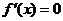 的根
的根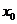 的左右的符号:“左正右负”
的左右的符号:“左正右负”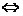
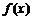 在
在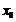 处取极大值;“左负右正”
处取极大值;“左负右正”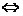
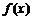 在
在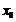 处取极小值。特别提醒:(1)
处取极小值。特别提醒:(1)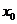 是极值点的充要条件是
是极值点的充要条件是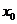 点两侧导数异号,而不仅是
点两侧导数异号,而不仅是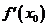 =0,
=0,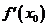 =0是
=0是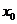 为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑
为极值点的必要而不充分条件。(2)给出函数极大(小)值的条件,一定要既考虑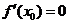 ,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记! 如(1)函数
,又要考虑检验“左正右负”(“左负右正”)的转化,否则条件没有用完,这一点一定要切记! 如(1)函数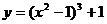 的极值点是 A、极大值点
的极值点是 A、极大值点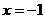 B、极大值点
B、极大值点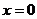 C、极小值点
C、极小值点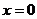 D、极小值点
D、极小值点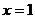 (答:C);(2)已知函数
(答:C);(2)已知函数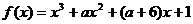 有极大值和极小值,则实数
有极大值和极小值,则实数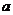 的取值范围是_____(答:
的取值范围是_____(答: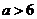 或
或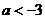 );(3)函数
);(3)函数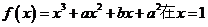 处有极小值10,则a+b的值为____(答:-7);(4)已知函数
处有极小值10,则a+b的值为____(答:-7);(4)已知函数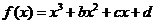 在区间[-1,2 ]上是减函数,那么b+c有最___值___(答:大,
在区间[-1,2 ]上是减函数,那么b+c有最___值___(答:大,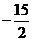 )
)
6、多项式函数的单调性:
(1)多项式函数的导数与函数的单调性:
①若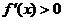 ,则
,则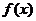 为增函数;若
为增函数;若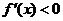 ,则
,则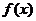 为减函数;若
为减函数;若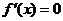 恒成立,则
恒成立,则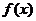 为常数函数;若
为常数函数;若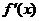 的符号不确定,则
的符号不确定,则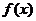 不是单调函数。
不是单调函数。
②若函数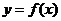 在区间(
在区间(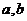 )上单调递增,则
)上单调递增,则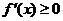 ,反之等号不成立;若函数
,反之等号不成立;若函数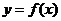 在区间(
在区间(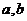 )上单调递减,则
)上单调递减,则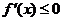 ,反之等号不成立。如(1)函数
,反之等号不成立。如(1)函数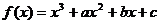 ,其中
,其中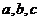 为实数,当
为实数,当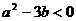 时,
时,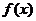 的单调性是______(答:增函数);(2)设
的单调性是______(答:增函数);(2)设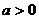 函数
函数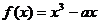 在
在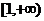 上单调函数,则实数
上单调函数,则实数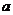 的取值范围______(答:
的取值范围______(答: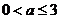 );(3)已知函数
);(3)已知函数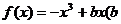 为常数)在区间
为常数)在区间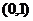 上单调递增,且方程
上单调递增,且方程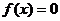 的根都在区间
的根都在区间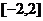 内,则
内,则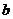 的取值范围是____________(答:
的取值范围是____________(答: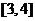 );(4)已知
);(4)已知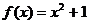 ,
,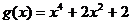 ,设
,设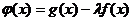 ,试问是否存在实数
,试问是否存在实数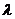 ,使
,使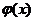 在
在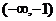 上是减函数,并且在
上是减函数,并且在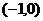 上是增函数?(答:
上是增函数?(答: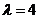 )
)
(2)利用导数求函数单调区间的步骤:(1)求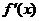 ;(2)求方程
;(2)求方程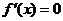 的根,设根为
的根,设根为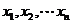 ;(3)
;(3)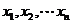 将给定区间分成n+1个子区间,再在每一个子区间内判断
将给定区间分成n+1个子区间,再在每一个子区间内判断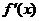 的符号,由此确定每一子区间的单调性。如设函数
的符号,由此确定每一子区间的单调性。如设函数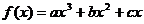 在
在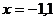 处有极值,且
处有极值,且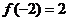 ,求
,求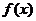 的单调区间。(答:递增区间(-1,1),递减区间
的单调区间。(答:递增区间(-1,1),递减区间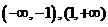 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com