
2.(1990年全国高考题)设椭圆的中心是坐标原点,长轴在x轴上,离心率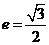 ,已知点
,已知点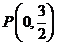 到这个椭圆上的点的最远距离是
到这个椭圆上的点的最远距离是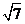 ,求这个椭圆的方程,并求椭圆上到点P的距离等于
,求这个椭圆的方程,并求椭圆上到点P的距离等于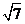 的点的坐标.
的点的坐标.
[答案与提示:1. 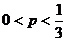 ; 2.
; 2.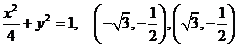 ]
]
1.(1988年全国高考题)直线L的方程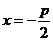 ,其中
,其中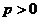 ;椭圆的中心为
;椭圆的中心为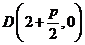 ,焦点在x轴上,长半轴长为2,短半轴长为1,它的一个顶点为
,焦点在x轴上,长半轴长为2,短半轴长为1,它的一个顶点为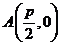 .问:p在那个范围内取值时,椭圆上有四个不同的点,他们中每一个点到点A的距离等于该点到直线L的距离.
.问:p在那个范围内取值时,椭圆上有四个不同的点,他们中每一个点到点A的距离等于该点到直线L的距离.
3.(1996年全国高考)已知ll,l2是过点P(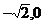 )的两条互相垂直的直线,且ll,l2与双曲线y2-x2=1各有两个交点,分别为A1,B1和A2,B2.
)的两条互相垂直的直线,且ll,l2与双曲线y2-x2=1各有两个交点,分别为A1,B1和A2,B2.
(I) 求l1的斜率k1的取值范围;
(II)若|A1B1|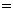
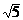 |A2B2|,求ll,l2的方程.
|A2B2|,求ll,l2的方程.
[答案与提示:1.略; 2.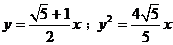 ; 3.(I)
; 3.(I)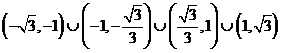 ; (II)
; (II) 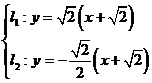
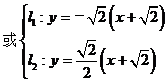 .]
.]
2.(1994年全国高考)已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.
1.(1991年全国高考)双曲线的中心在坐标原点O,焦点在x轴上,过双曲线右焦点且斜率为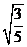 的直线交双曲线于P、Q两点.若
的直线交双曲线于P、Q两点.若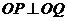 ,且
,且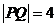 ,求双曲线的方程.
,求双曲线的方程.
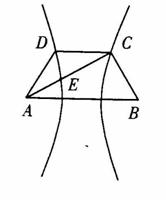
3.(2000全国理22)如图,已知梯形ABCD中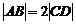 ,点E分有向线段
,点E分有向线段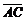 所成的比为
所成的比为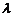 ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当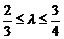 时,求双曲线离心率
时,求双曲线离心率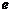 的取值范围.
的取值范围.
[答案与提示:1.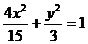 ;
2.
;
2.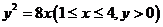 ;
3.
;
3.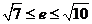 .]
.]
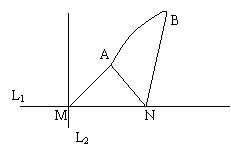
2.(1998年全国高考)如图, 直线L1和L2相交于点M,L1^L2, 点N ÎL1.以A、B为端点的曲线C上的任一点到L2的距离与到点N的距离相等.若DAMN为锐角三角形,|AM|= ,|AN| = 3,且|BN|=6.建立适当的坐标系,求曲线段C的方程.
1.(1993年全国高考题)在面积为1的△PMN 中,tanM = ,tanN = -2.建立适当的坐标系,求出以M,N为焦点且过点P的椭圆方程.
9. 原点关于直线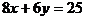 的对称点坐标是( )
的对称点坐标是( )
A. 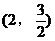 B.
B.
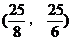 C.
C.
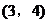 D.
(4,3)
D.
(4,3)
(1991年全国高考题)
8. 求过点P(0,2)且与点A(1,1),B(-3,1)等距离的直线l方程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com