
24. In fact, you _________ go outside at all. There’s a supermarket just downstairs.
A. couldn’t B. mustn’t C. needn’t D. shouldn’t
23. The news __________ Ding Junhui won the UK Championship isn’t surprising because he has the talent for snooker.
A. which B. that C. what D. when
22. It’s freezing cold outside. Put your coat on, _____________ you’ll get cold.
A. therefore B. however C. otherwise D. yet
第一节 单项填空 语法与词汇(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳答案。
21. I’m your cousin, John. You don’t have to go to ______ hotel. I can find you ______ bed in my apartment.
A. /; a B. a; the C. the; a D. the; the
(三)解答题
20.已知两圆C1∶x2+y2+4x-4y-5=0
C2∶x2+y2-8x+4y+7=0
(1)证明此两圆相切,并求过切点的公切线方程.
(2)求过点(2,3)且与两圆相切于上述切点的圆的方程.
21.(1)椭圆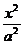 +
+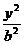 =1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积;
=1上一点P与两焦点 F1F2连线所成的角∠F1PF2=α,求△F1PF2的面积;
(2)将上题的椭圆变成双曲线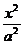 -
-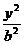 =1 ,求△F1PF2的面积.
=1 ,求△F1PF2的面积.
22.抛物线的顶点在原点,它的准线过双曲线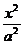 -
-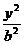 =1的一个焦点,并与双曲线的实轴垂直,又双曲线与抛物线的一个交点是(1.
5,
=1的一个焦点,并与双曲线的实轴垂直,又双曲线与抛物线的一个交点是(1.
5,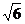 ),求抛物线和双曲线的方程.
),求抛物线和双曲线的方程.
23.已知椭圆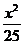 +
+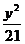 =1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由.
=1,左、右焦点分别为 F2、F1,右准线为L,问能否在椭圆上求得一点P,使│PF1│是P到L的距离d与│PF2│的比例中项?若能,求出P点坐标,若不能,说明理由.
24.试就k的取值(k∈R,且k≠4)讨论方程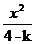 +(k-2)y2=1+k所表 示曲线的形状.
+(k-2)y2=1+k所表 示曲线的形状.
25.已知椭圆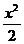 +
+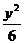 =1中有一内接△PAB,∠X
OP=60°,且kPA+kPB=0
=1中有一内接△PAB,∠X
OP=60°,且kPA+kPB=0
(1)求证:直线AB斜率是定值;
(二)填空题
16.直线xsinα+ycosα=m(常量α∈(0, )) 被圆x2+y2=2所截的弦长为
)) 被圆x2+y2=2所截的弦长为
 ,则m=________.
,则m=________.
17.设椭圆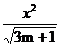 -
-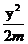 =1的准 线平行于x轴,则m的取值范围是________.
=1的准 线平行于x轴,则m的取值范围是________.
18.如果方程x2cos2θ+y2sinθ=1,表示椭圆,那么θ 角的取值范围是_________.
19.设双曲线C: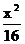 -
-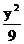 =1椭圆的焦点恰为双 曲线C实轴上的两个端点,椭圆与双曲线离心率为互为倒数,则此椭圆方程是________.
=1椭圆的焦点恰为双 曲线C实轴上的两个端点,椭圆与双曲线离心率为互为倒数,则此椭圆方程是________.
(一)选择题
1.“点M的坐标是方程f(x,y)=0的解”是“点M在方程f(x,y)=0曲线上”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既非充分又非必要条件
2.抛物线x=- 的焦点坐标是( )
的焦点坐标是( )
A.(0,1)
B.(-1,0) C.(0,- )
D.(-
)
D.(- ,0)
,0)
3.椭圆(1-m)x2-my2=1的长轴长是( )
A.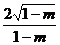 B.
B.  C.
C.
 D.
D.
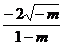
4.下列各对双曲线中,既有相同离心率又有相同渐近线的是( )
A.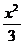 -y2=1和
-y2=1和 -
-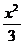 =1 B.
=1 B.
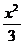 -y2=1和y2-
-y2=1和y2-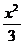 =1
=1
C.y2-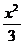 =1和x2-
=1和x2-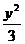 =1 D.
=1 D.
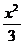 -y2=-1和
-y2=-1和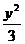 -
-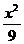 =1
=1
5.抛物线x2-4y=0上一点P到焦点的距离为3,那么P的纵坐标是( )
A.3 B.2 C.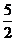 D.-2
D.-2
6.已知椭圆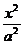 +
+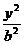 =1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )
=1 (a>b>0)的两 个焦点把夹在两条准线间的线段三等分,那么这个椭圆的离心率是( )
A.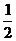 B.
B.
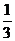 C.
C.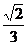 D.
D.
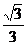
7.圆x2+y2-2axsinα-2bycosα-a2cos2α=0在x轴上截得的弦长是( )
A.2a B.2│a│ C. │a│ D.4│a│
│a│ D.4│a│
8.过双曲线的一个焦点,有垂直于实轴的弦PQ,F′是另一个焦点,若∠PF′Q= ,则双曲线离心率是( )
,则双曲线离心率是( )
A. +2 B.
+2 B.
 +1 C.
+1 C.
 D.
D.  -1
-1
9.抛物线y2+4y-4x=0的准线方程是( )
A.x=0 B.y=0 C.x=-2 D.y=-2
10.椭圆的两准线方程分别为x=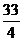 ,x=-
,x=-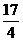 ,一个 焦点坐标为(6,2),则椭圆方程是( )
,一个 焦点坐标为(6,2),则椭圆方程是( )
A.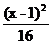 +
+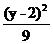 =1 B.
=1 B.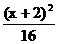 +
+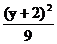 =1
=1
C.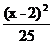 +
+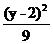 =1 D.
=1 D.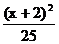 +
+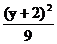 =1
=1
11.设双曲线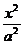 -
-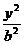 =1的两条渐近线含 实轴的夹角为θ,而离心率e∈[
=1的两条渐近线含 实轴的夹角为θ,而离心率e∈[ ,2],则θ的取值范围是( )
,2],则θ的取值范围是( )
A.[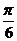 ,
, ]
B.[
]
B.[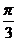 ,
, ] C.[
] C.[ ,
,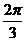 ] D.[
] D.[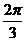 ,π]
,π]
12.椭圆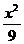 +
+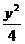 =1的弦AB被点(1,1)平分,则 AB所在的直线方程是( )
=1的弦AB被点(1,1)平分,则 AB所在的直线方程是( )
A.4x-9y-11=0 B.4x+9y-13=0 C.9x+4y-10=0 D.9x-4y-5=0
13.和x轴相切,且和圆x2+y2=1外切的动圆圆心的轨迹方程是( )
A.x2=2y+1 B.x2=-2y+1 C.x2=2y+1或x2=-2y+1 D.x2=2│y│+1
14.如果椭圆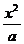 +
+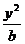 =1 (a>b>0)和曲线
=1 (a>b>0)和曲线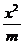 +
+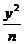 =1(m>0,n>0)有相同的焦点F1和F2 ,P是这两条曲线的交点,则│PF1│·│PF2│的值是( )
=1(m>0,n>0)有相同的焦点F1和F2 ,P是这两条曲线的交点,则│PF1│·│PF2│的值是( )
A.a-m
B. (a-m) C.a2-m2
D.
(a-m) C.a2-m2
D.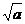 -
-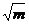
15.已知0<a<1<b,那么曲线a2x2-a2y2=logab是( )
A.焦点在x轴的双曲线 B.焦点在y轴的椭圆
C.焦点在x轴的等轴双曲线 D.焦点在y轴的等轴双曲线
(八)综合例题赏析
例9 设集合M={x|x>2|},P={x|x<3|},那么 “x∈M或x∈P”是“x∈M∩P”的( )
A.充分非必要条件 B.必要非充分条件 C.充分必要条件 D.非充分也非必要条件
解:M∪N=R,M∩N={2<x<3}
∴x∈M∩P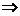 x∈M或x∈N.
x∈M或x∈N.
∴应选B.
例10 已知直线x=a(a>0)和圆(x-1)2+y2=4相切 ,那么a的值是( )
A.5 B.4 C.3 D.2
解:r=2,圆心(1,0),a>0,∴a=3
应选C.
例11 设圆满足:①截y轴所得的弦长为2;②被x轴分成 的两段弧,其弧长的比为3∶1在满足条件①、②的所有圆中,求圆心到直线l∶x-2y=0的距 离最小的圆的方程
解:设所求圆的圆心P(a,b)半径r
由题设知,P到x,y轴的距离分别为|b|,|a|,且圆P截x轴的弦所对圆心角为90°,故其弦 长为 r,有r2=2b2
r,有r2=2b2
由“圆P截y轴所得弦长为2”有r2=a2+1
∴2b2-a2=1
P(a,b)到直线x-2y=0的距离为
d=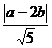 ,得
,得
5d2=|a-2b|2=a2+4b2-4ab≥a2+4b2-2(a2+b2)
2b2-a2=1
当且仅当a=b时上式等号成立,此时5d2=1从而d取得最小值
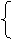
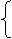
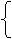 a=b
a=1
a=-1
a=b
a=1
a=-1
由此有 解得 或
2b2-a2=1 b=1 b=-1
又由r2=2b2,得r2=2.
∴所求圆方程是(x-1)2+(y-1)2=2,或(x+1)2+(y+1)2=2
例12 自点A(-3,3)发出的光线L射到x轴上,被x轴反射,其反射光线所在直线与圆x2+y2-4x-4y+7=0相切,求光线L所在的直线方程.
解:设反射光线为L′
∵L和L′关于x轴对称,L过点A(-3,3),点A关于x轴的对称点A′(-3,-3),
∴L′过A(-3,-3)
设L′的斜率为k,则L′的方程为
y-(-3)=k(x-(-3)],即kx-y+3k-3=0,
已知圆方程即(x-2)2+(y-2)2=1,圆心O的坐标为(2,2),半径r=1
∵L′和已知圆相切,做O′到L′的距离等于半径r=1
即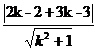 =
=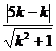 =1
=1
整理得12k2-25k+12=0
解得k= 或k=
或k=
∴L′的方程为y+3= (x+3);或y+3=
(x+3);或y+3= (x+3).即4x-3y+3=0,或3x- 4y-3
(x+3).即4x-3y+3=0,或3x- 4y-3
∵L和L′关于x轴对称
∴L的方程为4x+3y+3=0,或3x+4y-3=0.
例13 设椭圆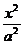 +
+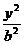 =1 (a>b>0) 的右焦点为F1,右准线为l1.若过F1且垂直于x轴的弦的长等于点F1到l1的距离, 则椭圆的离心率是_________.
=1 (a>b>0) 的右焦点为F1,右准线为l1.若过F1且垂直于x轴的弦的长等于点F1到l1的距离, 则椭圆的离心率是_________.
解:
例14 已知椭圆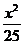 +
+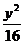 =1上一点P到椭圆一个焦点距离为3,则P到另一焦点的距离为( )
=1上一点P到椭圆一个焦点距离为3,则P到另一焦点的距离为( )
A.2 B.3 C.5 D.7
解:a2=25,a=5,2a=10.
此椭圆上的点到两焦点的距离之和为10
∴点P到另一焦点的距离为10-3=7.
应选D.
例15 设双曲线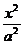 -
-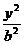 =1 (0<a<b)的半焦距为C,直线1过(a,0),(0,b)两点,已知原点到直线1的距离为
=1 (0<a<b)的半焦距为C,直线1过(a,0),(0,b)两点,已知原点到直线1的距离为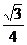 c,则双曲线的离心率为( )
c,则双曲线的离心率为( )
A.2. B. C.
C.
 D.
D.

解:∵直线1过(a,0),(0,b),
∴1的方程为 +
+ =1,
=1,
即bx+ay-ab=0
∵原点(0,0)到1的距离为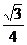 c,由点到直线的距离公式 ,得
c,由点到直线的距离公式 ,得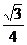 c=
c= 又0<a<b,双曲线中c2=a2+b2,
又0<a<b,双曲线中c2=a2+b2,
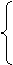 ∴c2=a2+b2
∴c2=a2+b2
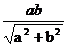 =
=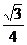 ,得ab=
,得ab=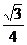 ,
,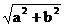 =
=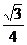 ·(a2+b2),
·(a2+b2),
整理得 a2-4ab+
a2-4ab+ b2=0,b=
b2=0,b= a.
a.
∴c2=a2+b2=4a2,c=2a,e= =2.
=2.
应选A.
例16 设F1和F2为双曲线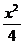 -y2 =1的两个焦点,点P在双曲线上且满足∠F1PF2=90°.则△F1PF2的面积是( )
-y2 =1的两个焦点,点P在双曲线上且满足∠F1PF2=90°.则△F1PF2的面积是( )
A.1 B. C.2
D.
C.2
D.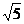
解:由已知可得,F1(-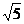 ,0),F2(
,0),F2(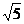 ,0)
,0)
∴|F1F2|=2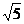 ,|F1F2|2=20
,|F1F2|2=20
由∠F1PF2=90°,
得20=|F1F2|2=|PF1|2+|PF2|2 ①
由双曲线定义得︳PF1︳-︳PF2︳=2a=4,平方得
|PF1|2+|PF2|2-2|PF1|·︳PF1|=16 ②
①-②得2|PF1|·|PF2|=4
∴S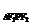 =
=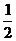 |PF1|·|PF2|
|PF1|·|PF2|
应选A.
例17 双曲线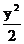 -x2=1的两个焦点坐标是______.
-x2=1的两个焦点坐标是______.
解:(0, ),(0,-
),(0,- )
)
例18 如果双曲线的实半轴长为2,焦距为6,那么该双曲线的离心率是( )
A.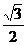 B.
B.
 C.
C.
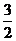 D.2
D.2
解:由题设知a=2,c=3.
∴e =
=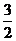 .
.
应选C.
例19 已知点(-2,3)与抛物线y2=2px(p>0)的焦点 的距离是5,则p=________.
解:y2=2px的焦点坐标是(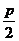 ,0),
,0),
∴5=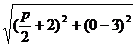
解出p=4.
例20 直线l过抛物线y2=a(x+1)(a>0)的焦点,并 且与x轴垂直,若l被抛物线截得的线段长为4,则a=_______.
解:设抛物线焦参数为p,则a=2p(p>0).
l是过焦点的直线且垂直于x轴即垂直于抛物线y2=a(x+1)的对称轴.
∴l被抛物线截得的线段即正焦弦长.
∴4=2p=a,即a=4.
例21 抛物线y2=4x的弦AB垂直于x轴,若AB的长为4 ,则焦点到AB的距离为_________.
,则焦点到AB的距离为_________.
解:由AB⊥x轴,│AB│=4 ,可设A(x1,2
,可设A(x1,2 ).
).
∵A(x1,2 )在抛物线y2=4x上,
)在抛物线y2=4x上,
∴(2 )2=4x1,得x1=3.
)2=4x1,得x1=3.
又y2=4x的焦点F的坐标为(1,0),
∴F到AB的距离为3-1=2.
例22 焦点在(-1,0),顶点在(1,0)的抛物线方程是( )
A.y2=8(x+1) B.y2=-8(x+1) C.y2=8(x-1) D.y2=-8(x-1)
解:设抛物线焦参数为p,则焦点和顶点的距离是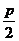 ,
,
即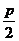 =
=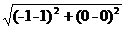 =2,得p=4.
=2,得p=4.
又抛物线顶点坐标为(1,0),焦点是(-1,0),
∴y2=-8(x-1)为所求.
应选D.
例23 曲线2y2+3x+3=0与曲线x2+y2-4x-5=0的公共 点的个数是( )
A.4 B.3 C.2 D.1
解:由2y2+3x+3=0,得y2=-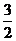 x-
x-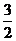 ≥0,
≥0,
∴x≤-1.
把y2=-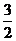 x-
x-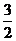 代入x2+y2-4x-5=0,得
代入x2+y2-4x-5=0,得
x2-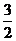 x-
x-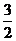 -4x-5=0,即2x2-11x-13=0
-4x-5=0,即2x2-11x-13=0
即(2x-13)(x+1)=0,∴x=-1(舍x=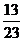 ).
).
把x=-1代入2y2+3x+3=0,得y=0.
∴交点为(-1,0),即只有一个交点.
应选D.
例24 设曲线C的方程是y=x3-x,将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C1.
(1)写出曲线C1的方程;
(2)证明曲线C与C1关于点A(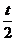 ,
,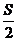 )对称;
)对称;
(3)如果曲线C与C1有且仅有一个公共点,证明S=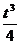 -t且t≠0.
-t且t≠0.
解:(1)曲线C1的方程为
y=(x-t)3-(x-t)+s
(2)在曲线C上任取点B1(x1,y1),设B2(x2,y2)是B1关于点A的对称点,则有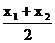 =
=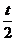 ,
,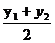 =
= ,
,
∴x1=t-x2,y1=s-y2
代入曲线C的方程,得x2和y2满足方程:
S-y2=(t-t2)3-(t-x2),
即y2=(x2-t)2-(x2-t)+s,
可知点B(x2-y2)在曲线C1上
反过来,同样可以证明,在曲线C1上的点关于点A的对称点在曲线C上,
∴曲线C与C1关于点A对称.
(3)∵曲线C与C1有且仅有一个公共点,
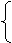 y=x2-x
y=x2-x
∴方程组 ,有且仅有一组解.
y=(x-t)3-(x-t)+S
消去y,整理得
3tx2-3t2x+(t3-t-S)=0,
这个关于x的一元二次方程有且仅有一个根
∴t≠0,并且其根的判别式
Δ=9t4-12t(t3-t-S)=0.
 t≠0
t≠0
即
t(t3-4t-4S)=0
∴S=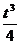 -t且t≠0
-t且t≠0
例25 已知l1,l2是过点P(- ,0 )的 两条相互垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1,B1和A2,B2,
,0 )的 两条相互垂直的直线,且l1、l2与双曲线y2-x2=1各有两个交点,分别为A1,B1和A2,B2,
(1)求l1的斜率k1的取值范围;
(2)若A1恰是双曲线的一个顶点,求│A2B2│的值.
解:(1)依题意,l1,l2的斜率都存在,
∵l1过点P(- ,0)且与y2-x2=1有两交点,
,0)且与y2-x2=1有两交点,
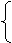 y=k1(x+
y=k1(x+ )(k1≠0)
)(k1≠0)
∴ ①有两个不同的解.
y2-x2=1
消y整理得
(k21-1)x2+2 k21x+2k21-1=0. ②
k21x+2k21-1=0. ②
若k21-1=0,则方程组①只有一解,与题设“l1和双曲线有两交点”矛盾.
∴k21-1≠0,即│k│≠1.
②的根的判别式为
Δ1=(2 k21)2-4(k21-1)·(2k21-1)
k21)2-4(k21-1)·(2k21-1)
=4(3k21-1).
设l2的斜率为k2,因l2和双曲线有两交点,
 y=k2(x+
y=k2(x+ )(k2≠0)
)(k2≠0)
∴方程组 ③有两不同解.
y2-x2=1
在③中消y整理得
(k22-1)x2+2 k22x+2k22-1=0. ④
k22x+2k22-1=0. ④
同理有│k2│≠1,Δ2=4(3k22-1).
由已知l1⊥l2,得k1·k2=-1.
∴l1,l2与双曲线各有两个交点,等价于

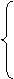 3k21-1>0
3k21-1>0
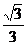 <│k1│<
<│k1│<
3k22-1>0 解得
k1·k2=-1 │k1│≠1
│k1│≠0,│k2 │≠1,
∴k1∈(- ,-1)∪(-1,-
,-1)∪(-1,-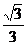 )∪(
)∪(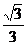 ,1)∪(1,
,1)∪(1, ).
).
(2)双曲线y2-x2=1的顶点为(0,1),(0,-1).
即A1(0,1)时,有
k1·(0+ )=1,得k1=
)=1,得k1=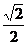 ,k2 =-
,k2 =-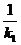 =-
=- .
.
将k2=- 代入方程④得x2+4
代入方程④得x2+4 x+3=0 ⑤
x+3=0 ⑤
记l2与双曲线的两交点为A2(x1,y1)、B2(x2,y2),
则│A2B2│2=(x1-x2)2+(y1-y2)2=3(x1-x2)2
=3((x1+x2)2-4x1x2)
由⑤知,x1+x2=-4 ,x1·x2=3,
,x1·x2=3,
∴│A2B2│2=3((-4 )2-4×3)=60,
)2-4×3)=60,
│A2B2│=2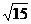 .
.
当取A1(0,-1)时,由双曲线y2-x2=1关于x轴的对称性,知│A2B2│=2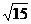 .
.
∴l1过双曲线一顶点时,│A2B2│=2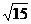 .
.
例26 已知椭圆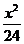 +
+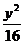 =1,直线L∶
=1,直线L∶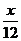 +
+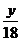 =1,P是L上
一 点,射线OP交椭圆于R,又点Q在OP上且满足│OQ│·│OP│=│OR│2,当点P在l上移动
时,求点Q的轨迹方程,并说明轨迹是什么曲线.
=1,P是L上
一 点,射线OP交椭圆于R,又点Q在OP上且满足│OQ│·│OP│=│OR│2,当点P在l上移动
时,求点Q的轨迹方程,并说明轨迹是什么曲线.
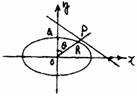
解:如图.
由题设知Q不在原点,设P、R、Q的坐标分别为(xP,yP)、(xR,yR)、(x,y)其中x ,y不同时为零.
当点P不在y轴上时,由于点R在椭圆上及点O、Q、R共线,得方程组;

 +
+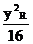 =1
x2R=
=1
x2R=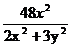 ①
①
,解得
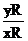 =
=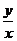 y2R=
y2R= ②
②
由于点P在直线l上及点O、Q、P共线,得方程组:


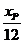 +
+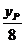 =1
xP=
=1
xP=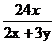
③,解得 ④
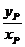 =
=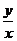 yP=
yP=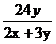
当点P在y轴上时,经检验①-④也成立.
∵│OQ│·│OP│=│OR│2
∴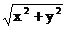 ·
·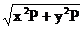 =(
=(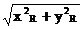 )2,
)2,
将(1)-(4)代入上式,化简整理得
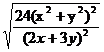 =
=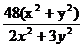 .
.
因x与xP同号或y与yP同号,以及③、④知2x+3y>0,
∴点Q的轨迹方程为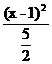 +
+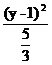 =1.其中(x,y不同时为零)
=1.其中(x,y不同时为零)
点Q的轨迹是以(1,1)为中心,长短半轴分别为 和
和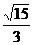 且长轴平行于x轴的椭圆.
且长轴平行于x轴的椭圆.
解法二:由题设知点Q不在原点.
设P、R、Q的坐标分别为(xP,yP),(xR,yR),(x,y)其中x,y不同时为零.
设OP写x轴正方向的夹角为α,则有
xP=│OP│cosα,yP=│OP│sinα;
xR=│OR│cosα,yR=│OP│sinα;
x=│OQ│cosα,y=│OQ│sinα;
又│OP│·│OQ│=│OR│2,可得
 xP=
xP=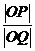 x
x2R=
x
x2R=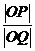 x2
x2
① ②
yP=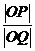 y
y2R=
y
y2R=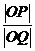 y2
y2
∵点P在直线l上,点R在椭圆上,

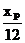 +
+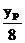 =1
=1
∴ ,将(1)、(2)代 入,得
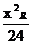 +
+ =1
=1
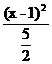 +
+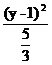 =1.(其中x,y不同时为零).
=1.(其中x,y不同时为零).
∴Q点的轨迹是以(1,1)为中心,长短半轴分别为 和
和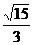 且长轴平行于x轴的椭圆(去掉坐标原点).
且长轴平行于x轴的椭圆(去掉坐标原点).
例27 已知直线l过坐标原点,抛物线C的顶点在原点、焦 点在x轴正半轴上,若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线的方程.
解法一:如图.
由题意可设抛物线C的方程为y2=2px (p>0),且x轴和y轴不是所求直线,又l过原点,所 以可设l的方程y=kx (k≠0) ①
 设A′、B′分别是A、B关于l的对称点,则有,
设A′、B′分别是A、B关于l的对称点,则有,
A′A⊥l,直线AA′的方程为
y=- (x+1).
②
(x+1).
②
由①、②联立得AA′与l的交点M的坐标为(-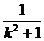 ,-
,-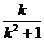 ).
).
由M为AA′的中点,得点A′的坐标为,
xA′=2(-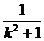 )+1=
)+1=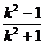 ,
,
yA′=2(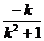 )+0=-
)+0=-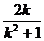 ③
③
同理可得点B的坐标为(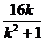 ,
,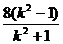 ).
).
∵A′、B′均在抛物线y2=2px (R>0)上,
∴(-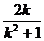 )2=2p·
)2=2p·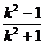 ,知k≠±1 ,p=
,知k≠±1 ,p=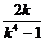 .
.
同理(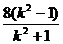 )2=2p·
)2=2p·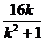 ,得p=
,得p= 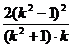 .
.
∴ =
=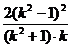 ,
,
整理得k2-k-1=0.
解得k1= ,k2=
,k2=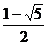 .
.
但当k=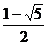 时,xA′=-
时,xA′=- <0,与A′在抛物线y2=2px上矛盾,故舍去.
<0,与A′在抛物线y2=2px上矛盾,故舍去.
把k= 代入p=
代入p= =
=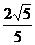 .
.
∴直线方程为y= x,抛物线方程为y2=
x,抛物线方程为y2=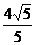 x.
x.
解法二:设点A、B关于直线l的对称点A′(x1,y1)、B′(x2,y2),则有
│OA′│=│OA│=1,│OB′│=│OB│=8
设x轴正向到OB′的转角为α,则有
x2=8cosα,y2=8sinα ①
∵A′,B′是A,B关于直线l的对称点,
又∠BOA是直角,
∴∠B′OA′为直角,得
x1=cos(α- )=sin α,y1=sin(α-
)=sin α,y1=sin(α- )=-cosα ②
)=-cosα ②
由题意知,x1>0,x2>0,故α为第一象限角.
∵A′,B′都在抛物线y2=2px上,
∴cos2α=2p·sinα,64sin2α=2p· cosα
∴8sin3α=cos3α,得2sinα=cosα
解得sinα= ,cosα=
,cosα=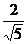 .
.
代入cos2α=2psinα,得p=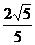 .
.
∴抛物线方程为y2=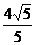 x.
x.
∵直线l平分∠BOB′,
∴l的斜率k=tg(α+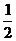 (
( -α))=tg(
-α))=tg(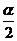 +
+ )
)
=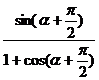 =
=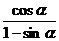 =
= .
.
∴ 直线l的方程为y= x.
x.
例28 在面积为1的△PMN中,tgM=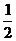 ,tgN=-2,建立适当的坐标系,求出M、N为焦点且过点P的椭圆方
程.
,tgN=-2,建立适当的坐标系,求出M、N为焦点且过点P的椭圆方
程.
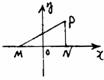 解:如图
解:如图
以MN所在直线为x轴,以线段MN的垂直平分线为y轴建立坐标系.
设以M、N为焦点且过P点的椭圆的方程为
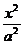 +
+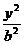 =1 (a>b>0)
=1 (a>b>0)
点M、N的坐标分别为(-c,0)、(c,0).
由tgM=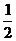 ,tg∠PNx=tg(π-∠MNP)=2,得
,tg∠PNx=tg(π-∠MNP)=2,得
直线PM和直线PN的方程分别为
y=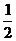 (x+c),y=2(x-c).
(x+c),y=2(x-c).
 x=
x=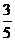 c
c
将两方程联立得
,即P(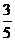 c,
c,  c).
c).
y= c
c
已知△MNP的面积为1,
∴1=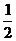 |MN|·y?P=
|MN|·y?P=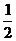 ·2c·
·2c· c=
c= c2,
c2,
得c=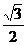 ,P(
,P(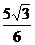 ,
, ).
).
∵|PM|= =
=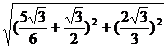
=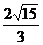 ,
,
|PN|=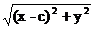 =
=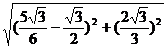
=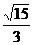 ,
,
∴2a=|PM|+|PN|=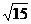 ,a=
,a=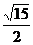 ,
,
b2=a2-c2=(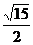 )2-(
)2-(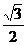 )2=3 .
)2=3 .
∴ +
+ =1为所求椭圆方程.
=1为所求椭圆方程.
例29 设抛物线经过两点(-1,6)和(-1,-2),对称轴与x 轴平行,开口向右,直线y=2x+7被抛物线截得线段长是4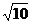 ,求抛物线的方 程.
,求抛物线的方 程.
解:设所求抛物线的顶点坐标为(x0,y0),由题设可设所求抛物线方程为(y-y0)2=2 p(x-x0)(p>0)
∵(-1,6),(-1,-2)在抛物线上,
∴抛物线的对称轴为y=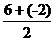 =2,即y0=2,抛物线方程化为(y-2)2=2p(x -x0) ①
=2,即y0=2,抛物线方程化为(y-2)2=2p(x -x0) ①
把(-1,-2)代入,得2px0=-2p-16 ②
设直线和抛物线两交点坐标为(x1,y1),(x2,y2).
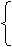 (y-2)2=2p(x-x0)
(y-2)2=2p(x-x0)
由 ,得
y=2x+7
4x2+(20-2p)x+(25+2px0)=0,
将①:2px0=-2p-16代入上面方程,得
4x2+(20-2p)x+(199-2p)=0,
x1,x2是方程的两根,由根与系数的关系得x1+x2=5-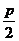 ,x1·x2=
,x1·x2=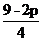 .
.
∴|x1-x2|=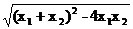 =
=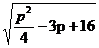
∴4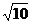 =
= =
=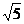 |x1-x2|
|x1-x2|
=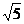 ·
·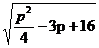
化简整理得p2-12p-64=0,
即(p-16)(p+4)=0,又p>0,
∴p=16. 由2px0=-2p-16,得x0=-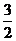 . ∴(y-2)2=32(x+
. ∴(y-2)2=32(x+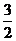 )为所求抛物线方程.
)为所求抛物线方程.
例30 已知椭圆的中心在坐标原点O,焦点在坐标轴上,直线y=x+1 与该椭圆相交于P和Q,且OP⊥OQ,|PQ|= ,求椭圆的方程.
,求椭圆的方程.
解:设所求椭圆的方程为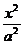 +
+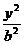 =1.
=1.
依题意知,点P、Q的坐标满足方程组:
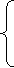
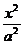 +
+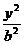 =1 ①
=1 ①
(1)y=x+1 ②
将②代入①,整理得
(a2+b2)x2+2a2x+a2(1-b2)=0, ③
设方程③的两个根分别为x1、x2,则直线y=x+1和椭圆的交点为,
P(x1,x1+1),Q(x2,x2+1)
由题设OP⊥OQ,|OP|= ,可得
,可得

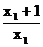 ·
· =-1
=-1
(x2-x1)2+((x2+1)-(x1+1))2=( )2.
)2.
整理得
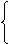 (x1+x2)+2x1x2+1=0 ④
(x1+x2)+2x1x2+1=0 ④
4(x1+x2)2 -16x1x2-5=0 ⑤
解这个方程组,得
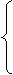
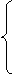 x1x2=
x1x2= x1x2=-
x1x2=-
或
x1+x2=-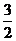 x1+x2=-
x1+x2=-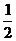
根据根与系数的关系,由(3)式得

 =
=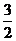
 =
=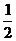
(Ⅰ) 或 (Ⅱ)
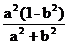 =
=
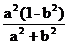 =-
=-
解方程组(Ⅰ)、(Ⅱ)得
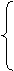
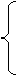 a2=2
a2=
a2=2
a2=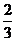
或
b2=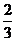 b2=2
b2=2
故所求椭圆方程为
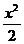 +
+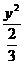 =1,或
=1,或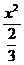 +
+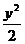 =1.
=1.
例31 已知双曲线C的实半轴长和虚半轴长的乘积为 ,C的两个焦点分别为F1、F2,直线L过F2且与直线F1F2的夹角为
,C的两个焦点分别为F1、F2,直线L过F2且与直线F1F2的夹角为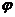 ,tg
,tg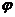 =
=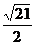 ,L与线段F1F2的垂直平分线的交点是P,线段PF2与双曲线C的交点为Q(且|PQ|∶|PF2=2∶1),求双曲线的方程.
,L与线段F1F2的垂直平分线的交点是P,线段PF2与双曲线C的交点为Q(且|PQ|∶|PF2=2∶1),求双曲线的方程.
解:如图,
以直线F1F2为x轴,线段F1F2的垂直平分线为y轴建立坐标系.
设双曲线C的方程为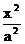 -
-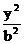 =1 (a>b>0)
=1 (a>b>0)
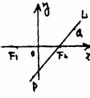 设F1,F2的坐标分别为(-c,0)、(c,0),其中C=
设F1,F2的坐标分别为(-c,0)、(c,0),其中C=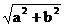 ,则点P的坐标为(0,-
,则点P的坐标为(0,-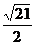 ,c).
,c).
由线段的定比分点公式可得Q点的坐标为(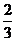 c,-
c,- 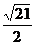 c).
c).
将Q点坐标代入双曲线方程得
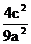 -
-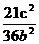 =1,整理得
=1,整理得
16(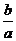 )4-41(
)4-41(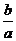 )2-21=0
)2-21=0
解得(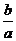 )2=3或(
)2=3或(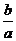 )2=-
)2=-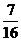 (舍去)
(舍去)
由(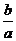 )2=3和题设ab=
)2=3和题设ab= ,解得a=1,b=
,解得a=1,b= .
.
故所求双曲线方程为x2-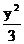 =1.
=1.
例32 已知点P在直线x=2上移动,直线l通过原点且OP垂直 ,过点A(1,0)和点P的直线m和直线l交于点Q,求点Q的轨迹方程,并指出该轨迹的名称和它 的焦点坐标.
解:设点P的坐标为(2,y1),则直线OP的斜率
kOP=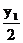 .
.
∵l⊥直线OP.
∴直线l的斜率k1满足kOP·k1=-1,即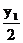 ·k1=-1,得k 1=-
·k1=-1,得k 1=- .
.
又直线l过原点,所以l的方程为y=- x.
x.
∵直线m过点A(1,0),P(2,y1).
∴m的方程为y1x-y-y1=0
由l的方程得y1=-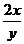 代入m的方程得-
代入m的方程得-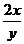 -x-y+
-x-y+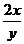 =0,即2x2+y2-2x=0.
=0,即2x2+y2-2x=0.
显然点Q与点A(1,0)不重合,故x≠1.
又2x2+y2-2x=0可化为
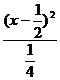 +
+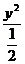 =1 (x≠1),
=1 (x≠1),
∴Q点的轨迹是挖去点(1,0)的椭圆,该椭圆的焦点坐标是(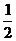 ,
,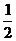 )和(
)和(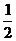 ,-
,-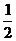 ).
).
例33 已知椭圆的焦点为F1(0,-1)和F2(0,1),直线 y=4是椭圆的一条准线.
(1)求椭圆方程;
(2)设点P在椭圆上,且│PF1│-│PF2│=1,求
tg∠F1PF2的值.
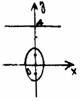 解:如图.
解:如图.
(1)设所求椭圆方程为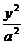 +
+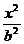 =1,(a> b>0)
=1,(a> b>0)
由F1(0,-1)和F2(0,1),知c=1,得a2=b2+1, ①
由一条准线方程为y=4知,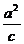 =4 ②
=4 ②
又a2=b2+c2 ③
由①、②、③解得a2=4,b2=3.
故所求椭圆方程为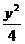 +
+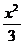 =1.
=1.
(2)由椭圆定义及a=2有│PF1│+│PF2│=4 ①
由题设有│PF1│-│PF2│=1 ②
解出│PF1│=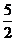 ,│PF2│=
,│PF2│=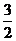 ,又│F1F2 │=2.
,又│F1F2 │=2.
在△PF1F2中,∠F1PF2=θ,
∴cosθ=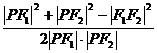 =
=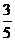 ,
,
从而sinθ=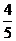 ,tgθ=
,tgθ= ,tg∠F1PF2=
,tg∠F1PF2= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com