
1.求证:数列{bn}为等比数列,并求出其通项公式;
13.(西南师大附中高2010级第五次月考)数列{an}中a1 = 2,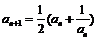 ,{bn}中
,{bn}中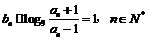 .
.
12.(江苏省苏州中学2010届高三上学期期中考试)已知函数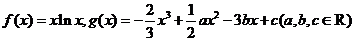 .
.
(1)若函数 是其定义域上的增函数,求实数
是其定义域上的增函数,求实数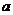 的取值范围;
的取值范围;
(2)若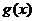 是奇函数,且
是奇函数,且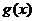 的极大值是
的极大值是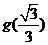 ,求函数
,求函数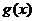 在区间
在区间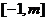 上的最大值;
上的最大值;
(3)证明:当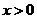 时,
时,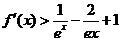 .
.
解:(1)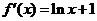 ,
,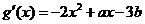 ,所以
,所以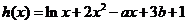 ,
,
由于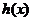 是定义域内的增函数,故
是定义域内的增函数,故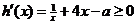 恒成立,
恒成立,
即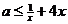 对
对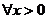 恒成立,又
恒成立,又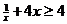 (
(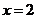 时取等号),故
时取等号),故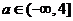 .
.
(2)由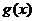 是奇函数,则
是奇函数,则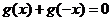 对
对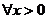 恒成立,从而
恒成立,从而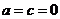 ,
,
所以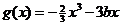 ,有
,有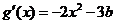 .
.
由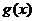 极大值为
极大值为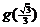 ,即
,即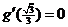 ,从而
,从而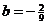 ;
;
因此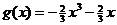 ,即
,即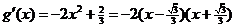 ,
,
所以函数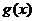 在
在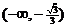 和
和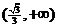 上是减函数,在
上是减函数,在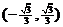 上是增函数.
上是增函数.
由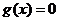 ,得
,得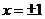 或
或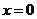 ,因此得到:
,因此得到:
当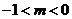 时,最大值为
时,最大值为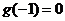 ;
;
当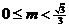 时,最大值为
时,最大值为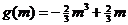 ;
;
当 时,最大值为
时,最大值为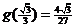 .
.
(3)问题等价于证明 对
对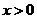 恒成立;
恒成立;
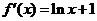 ,所以当
,所以当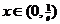 时,
时,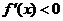 ,
,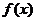 在
在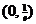 上单调减;
上单调减;
当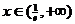 时,
时,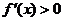 ,
,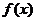 在
在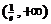 上单调增;
上单调增;
所以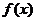 在
在 上最小值为
上最小值为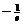 (当且仅当
(当且仅当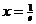 时取得)
时取得)
设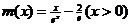 ,则
,则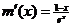 ,得
,得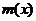 最大值
最大值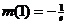 (当且仅当
(当且仅当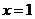 时取得),
时取得),
又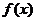 得最小值与
得最小值与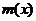 的最大值不能同时取到,所以结论成立.
的最大值不能同时取到,所以结论成立.
11.(福建省福州三中2010届高三上学期第三次月考)已知函数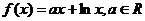 .(Ⅰ)求函数
.(Ⅰ)求函数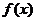 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点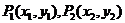 ,如果存在曲线上的点
,如果存在曲线上的点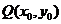 ,且
,且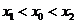 ,使得曲线在点
,使得曲线在点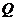 处的切线
处的切线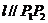 ,则称
,则称 为弦
为弦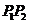 的伴随切线.特别地,当
的伴随切线.特别地,当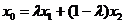
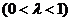 时,又称
时,又称 为
为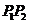 的
的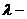 伴随切线.
伴随切线.
(i)求证:曲线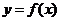 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ii)是否存在曲线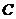 ,使得曲线
,使得曲线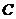 的任意一条弦均有
的任意一条弦均有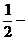 伴随切线?若存在,给
伴随切线?若存在,给
出一条这样的曲线,并证明你的结论;若不存在,说明理由.
(Ⅰ)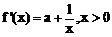 ………………………………………………… 2分
当
………………………………………………… 2分
当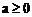 ,
,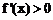 ,函数
,函数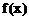 在
在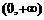 内是增函数,
内是增函数,
∴函数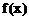 没有极值.……………………………………………… 3分
没有极值.……………………………………………… 3分
当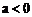 时,令
时,令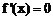 ,得
,得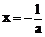 .
.
当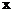 变化时,
变化时,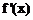 与
与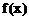 变化情况如下表:
变化情况如下表:
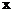 |
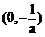 |
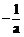 |
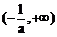 |
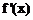 |
+ |
0 |
- |
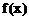 |
单调递增 |
极大值 |
单调递减 |
∴当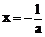 时,
时,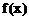 取得极大值
取得极大值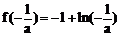 .
.
综上,当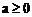 时,
时,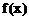 没有极值;
没有极值;
当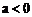 时,
时,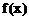 的极大值为
的极大值为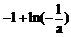 ,没有极小值. …… 5分
,没有极小值. …… 5分
(Ⅱ)(ⅰ)设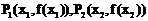 是曲线
是曲线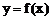 上的任意两点,要证明
上的任意两点,要证明
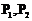 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点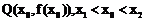 ,使得
,使得
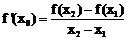 ,且点
,且点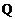 不在
不在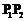 上. ……………… 7分
上. ……………… 7分
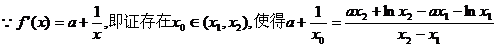
即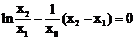 成立,且点
成立,且点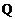 不在
不在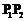 上. ………………… 8分
上. ………………… 8分
以下证明方程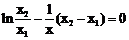 在
在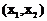 内有解.
内有解.
记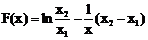 ,则
,则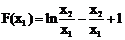 .
.
令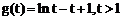 ,
,
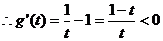
∴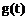 在
在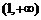 内是减函数,∴
内是减函数,∴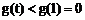 .
.
取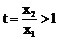 ,则
,则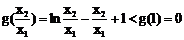 ,即
,即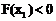 .… 9分
.… 9分
同理可证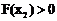 .∴
.∴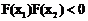 .
.
∴函数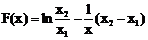 在
在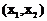 内有零点.
内有零点.
即方程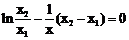 在
在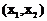 内有解
内有解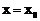 .……… 10分
.……… 10分
又对于函数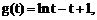 取
取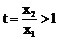 ,则
,则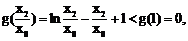
可知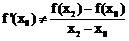 ,即点Q不在
,即点Q不在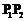 上.
上.
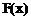 是增函数,∴
是增函数,∴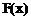 的零点是唯一的,
的零点是唯一的,
即方程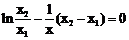 在
在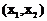 内有唯一解.
内有唯一解.
综上,曲线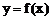 上任意一条弦均有伴随切线,并且伴随切线是唯一的.11分
上任意一条弦均有伴随切线,并且伴随切线是唯一的.11分
(ⅱ)取曲线C: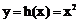 ,则曲线
,则曲线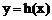 的任意一条弦均有
的任意一条弦均有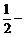 伴随切线.
伴随切线.
证明如下:
设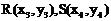 是曲线C上任意两点
是曲线C上任意两点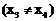 ,则
,则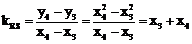 ,
,
又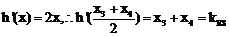 ,
,
即曲线C: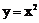 的任意一条弦均有
的任意一条弦均有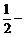 伴随切线. ………………14分
伴随切线. ………………14分
注:只要考生给出一条满足条件的曲线,并给出正确证明,均给满分.若只给曲线,没有给出正确的证明,不给分.
10.(广东省广州市2010届高三上学期期末调研)设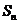 为数列
为数列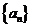 的前
的前 项和,对任意的
项和,对任意的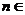 N
N ,都有
,都有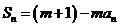
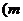 为常数,且
为常数,且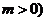 .
.
(1)求证:数列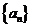 是等比数列;
是等比数列;
(2)设数列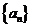 的公比
的公比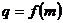 ,数列
,数列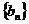 满足
满足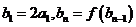
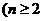 ,
,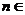 N
N
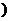 ,求数列
,求数列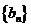 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求证:数列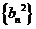 的前
的前 项和
项和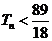 .
.
(1)证明:当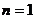 时,
时, ,解得
,解得 .……………………………………1分
.……………………………………1分
当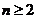 时,
时,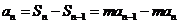 .…………………………………2分
.…………………………………2分
即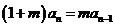 .
.
∵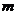 为常数,且
为常数,且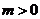 ,∴
,∴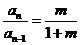
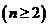 .……………………………3分
.……………………………3分
∴数列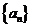 是首项为1,公比为
是首项为1,公比为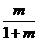 的等比数列.……………………………4分
的等比数列.……………………………4分
(2)解:由(1)得,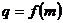
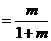 ,
,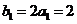 . ………………………5分
. ………………………5分
∵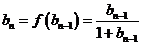 ,………………………………………………………6分
,………………………………………………………6分
∴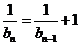 ,即
,即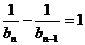
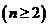 .……………………………………7分
.……………………………………7分
∴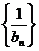 是首项为
是首项为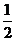 ,公差为1的等差数列.…………………………………………………………8分
,公差为1的等差数列.…………………………………………………………8分
∴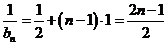 ,即
,即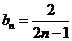 (
(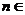 N
N ).……………………………9分
).……………………………9分
(3)证明:由(2)知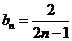 ,则
,则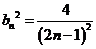 .………………………………10分
.………………………………10分
所以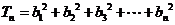
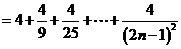 ,……………11分
,……………11分
当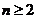 时,
时,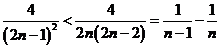 ,…………………12分
,…………………12分
所以
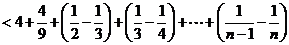
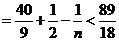 .……………………………………
.……………………………………
9.(福建省普通高中毕业班质量检查)已知函数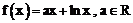
(Ⅰ)求函数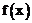 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点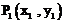 ,
,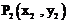 ,如果存在曲线上的点
,如果存在曲线上的点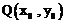 ,且
,且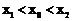 ,使得曲线在点
,使得曲线在点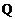 处的切线
处的切线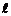 ∥
∥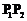 ,则称
,则称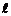 为弦
为弦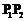 的伴随切线。特别地,当
的伴随切线。特别地,当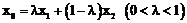 时,又称
时,又称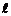 为
为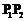 的λ-伴随切线。
的λ-伴随切线。
(ⅰ)求证:曲线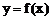 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有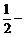 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
(Ⅰ)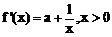 ………………………………………………………… 2分
………………………………………………………… 2分
当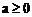 ,
,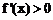 ,函数
,函数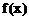 在
在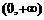 内是增函数,
内是增函数,
∴函数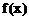 没有极值。 …………………………………………………… 3分
没有极值。 …………………………………………………… 3分
当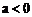 时,令
时,令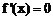 ,得
,得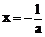 。
。
当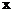 变化时,
变化时,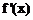 与
与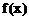 变化情况如下表:
变化情况如下表:
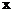 |
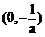 |
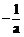 |
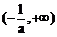 |
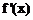 |
+ |
0 |
- |
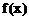 |
单调递增 |
极大值 |
单调递减 |
∴当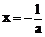 时,
时,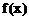 取得极大值
取得极大值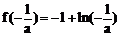 。
。
综上,当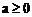 时,
时,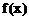 没有极值;
没有极值;
当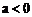 时,
时,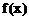 的极大值为
的极大值为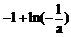 ,没有极小值。 ……………5分
,没有极小值。 ……………5分
(Ⅱ)(ⅰ)设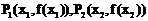 是曲线
是曲线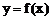 上的任意两点,要证明
上的任意两点,要证明
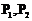 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点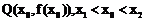 ,使得
,使得
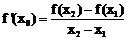 ,且点
,且点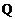 不在
不在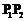 上。 ……………………7分
上。 ……………………7分
∵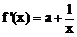 ,即证存在
,即证存在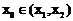 ,使得
,使得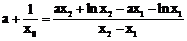 ,即
,即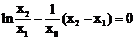 成立,且点
成立,且点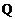 不在
不在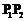 上。 …………………8分
上。 …………………8分
以下证明方程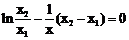 在
在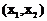 内有解。
内有解。
记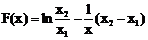 ,则
,则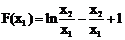 。
。
令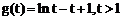 ,
,
∴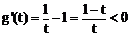 ,
,
∴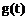 在
在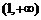 内是减函数,∴
内是减函数,∴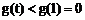 。
。
取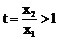 ,则
,则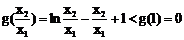 ,即
,即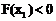 。……9分
。……9分
同理可证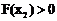 。∴
。∴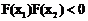 。
。
∴函数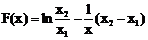 在
在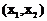 内有零点。
内有零点。
即方程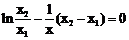 在
在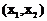 内有解
内有解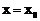 。………………10分
。………………10分
又对于函数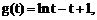 取
取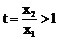 ,则
,则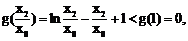
可知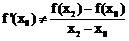 ,即点Q不在
,即点Q不在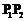 上。
上。
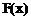 是增函数,∴
是增函数,∴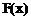 的零点是唯一的,
的零点是唯一的,
即方程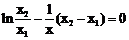 在
在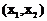 内有唯一解。
内有唯一解。
综上,曲线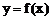 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。
…………………………………………………………………………… 11分
(ⅱ)取曲线C: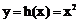 ,则曲线
,则曲线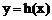 的任意一条弦均有
的任意一条弦均有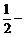 伴随切线。
伴随切线。
证明如下:
设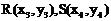 是曲线C上任意两点
是曲线C上任意两点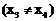 ,
,
则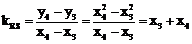 ,
,
又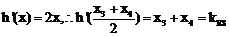 ,
,
即曲线C: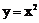 的任意一条弦均有
的任意一条弦均有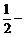 伴随切线。 …………………14分
伴随切线。 …………………14分
注:只要考生给出一条满足条件的曲线,并给出正确证明,均给满分。若只给曲
线,没有给出正确的证明,不给分。
解法二:
(Ⅰ)同解法一。
(Ⅱ)(ⅰ)设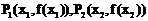 是曲线
是曲线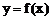 上的任意两点,要证明
上的任意两点,要证明
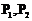 有伴随切线,只需证明存在点
有伴随切线,只需证明存在点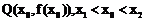 ,使得
,使得
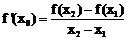 ,且点
,且点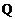 不在
不在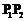 上。 …………………………… 7分
上。 …………………………… 7分
∵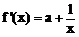 ,即证存在
,即证存在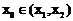 ,使得
,使得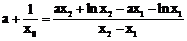 ,
,
即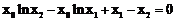 成立,且点
成立,且点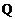 不在
不在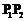 上。 …………… 8分
上。 …………… 8分
以下证明方程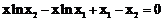 在
在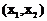 内有解。
内有解。
设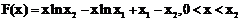 。
。
则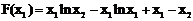 。
。
记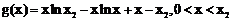 ,
,
∴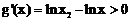 ,
,
∴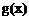 在
在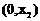 内是增函数,
内是增函数,
∴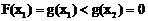 。 …………………………………………… 9分
。 …………………………………………… 9分
同理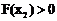 。
。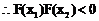 。
。
∴方程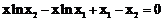 在
在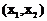 内有解
内有解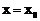 。 …………10分
。 …………10分
又对于函数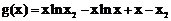 ,
,
∵ ,
,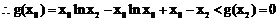 ,
,
可知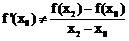 ,即点Q不在
,即点Q不在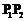 上。
上。
又 在
在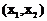 内是增函数,
内是增函数,
∴方程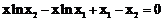 在
在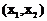 内有唯一解。
内有唯一解。
综上,曲线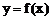 上任意一条弦均有伴随切线,并且伴随切线是唯一的。
上任意一条弦均有伴随切线,并且伴随切线是唯一的。
…………………………………………………………………………… 11分
(ⅱ)同解法一。
8.(湖南师大附中2010届高三第五次月考)如图,抛物线的顶点在坐标原点,且开口向右,点A,B,C在抛物线上,△ABC的重心F为抛物线的焦点,直线AB的方程为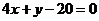 .
.
(Ⅰ)求抛物线的方程;
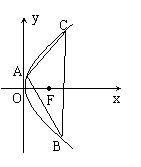 (Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由.
(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由.
[解](Ⅰ)设抛物线方程为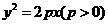 ,
,
联立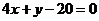 消去x,得
消去x,得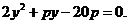 (2分)
(2分)
设点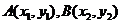 ,则
,则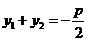 .
.
所以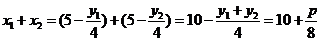 .
(4分)
.
(4分)
设点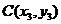 ,因为△ABC的重心为
,因为△ABC的重心为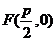 ,则
,则
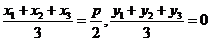 ,所以
,所以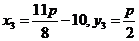 .
(5分)
.
(5分)
因为点C在抛物线上,则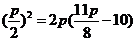 ,解得p=8,此时
,解得p=8,此时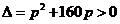 .
.
故抛物线方程为y2=16x. (6分)
(Ⅱ)设过定点M的动直线l的方程为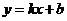
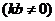 ,代入抛物线方程y2=16x,得
,代入抛物线方程y2=16x,得
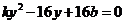 ,所以
,所以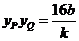 .
(8分)
.
(8分)
若以线段PQ为直径的圆经过坐标原点,则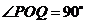 ,即
,即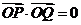 .
.
所以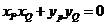 ,即
,即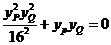 ,所以
,所以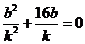 .
.
因为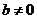 ,所以
,所以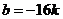 .
(10分)
.
(10分)
所以直线l的方程为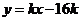 ,即
,即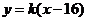 ,从而直线l必经过定点
,从而直线l必经过定点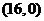 . (11分)
. (11分)
若直线l的斜率不存在,因为直线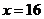 与抛物线的交点为
与抛物线的交点为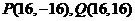 ,此时仍有
,此时仍有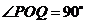 .故存在定点
.故存在定点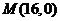 满足条件.
(13分)
满足条件.
(13分)
7.(哈三中2009-2010学年度上学期高三学年期末考试)已知函数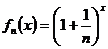
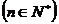 .
.
(Ⅰ) 比较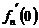 与
与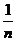 的大小;
的大小;
(Ⅱ) 求证: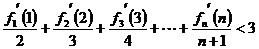 .
.
(Ⅰ)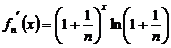
则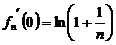 ,设函数
,设函数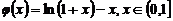
则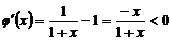 ,则
,则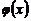 单调递减,
单调递减,
所以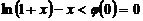 ,所以
,所以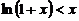
则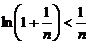 ,即
,即 ;
;
(Ⅱ)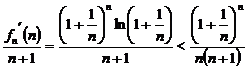 .
.
因为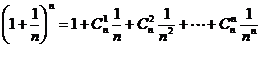
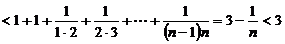
则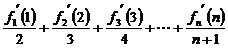
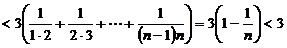
则原结论成立.
6.(崇文区2009-2010学年度第一学期期末统一练习)已知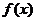 为二次函数,不等式
为二次函数,不等式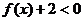 的解集为
的解集为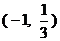 ,且对任意
,且对任意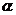 ,
,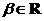 恒有
恒有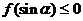 ,
,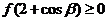 .数列
.数列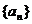 满足
满足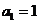 ,
,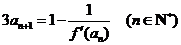
(Ⅰ)求函数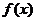 的解析式;
的解析式;
(Ⅱ)设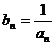 ,求数列
,求数列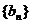 的通项公式;
的通项公式;
(Ⅲ)若(Ⅱ)中数列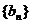 的前
的前 项和为
项和为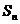 ,求数列
,求数列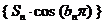 的前n项和
的前n项和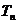 .
.
解:(Ⅰ)依题意,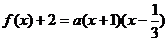
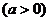 ,即
,即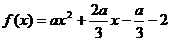
令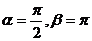 ,则
,则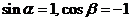 ,有
,有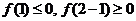 ,
,
得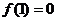 ,即
,即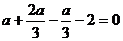 ,得
,得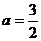 .
.
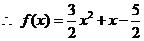 .
---------------- 4分
.
---------------- 4分
(Ⅱ)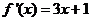 ,则
,则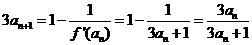
即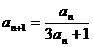 ,两边取倒数,得
,两边取倒数,得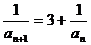 ,即
,即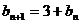 .
.
 数列
数列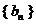 是首项为
是首项为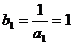 ,公差为
,公差为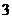 的等差数列.
的等差数列.
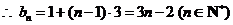 .
---------------- 9分
.
---------------- 9分
(Ⅲ)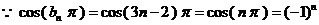
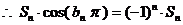
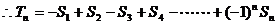 .
.
(1)当 为偶数时
为偶数时
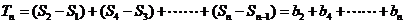
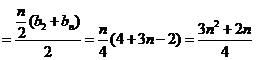
(2)当 为奇数时
为奇数时
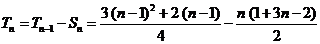
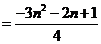
综上,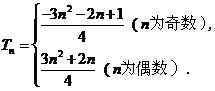 ----------------1 3分
----------------1 3分
5.(北京市西城区2010年高三年级抽样测试)已知曲线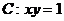 ,过C上一点
,过C上一点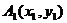 作斜率
作斜率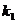 的直线,交曲线
的直线,交曲线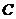 于另一点
于另一点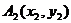 ,再过
,再过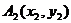 作斜率为
作斜率为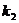 的直线,交曲线C于另一点
的直线,交曲线C于另一点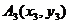 ,…,过
,…,过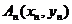 作斜率为
作斜率为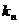 的直线,交曲线C于另一点
的直线,交曲线C于另一点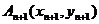 …,其中
…,其中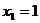 ,
,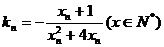
(1)求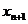 与
与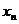 的关系式;(2)判断
的关系式;(2)判断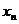 与2的大小关系,并证明你的结论;
与2的大小关系,并证明你的结论;
(3)求证: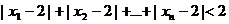 .
.
解:(1)由已知过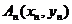 斜率为
斜率为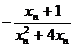 的直线为
的直线为
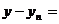
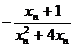
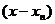 ,
,
直线交曲线C于另一点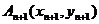
所以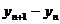 =
=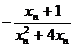
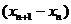 2分
2分
即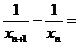
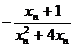
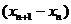 ,
,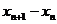 ≠0,
≠0,
所以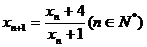 4分
4分
(2)解:当 为奇数时,
为奇数时,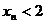 ;当n为偶数时,
;当n为偶数时,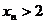 5分
5分
因为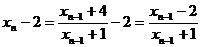 , 6分
, 6分
注意到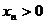 ,所以
,所以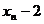 与
与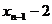 异号
异号
由于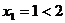 ,所以
,所以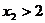 ,以此类推,
,以此类推,
当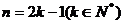 时,
时,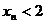 ;
;
当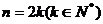 时,
时,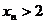 8分
8分
(3)由于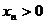 ,
,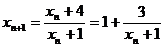 ,
,
所以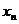 ≥1(
≥1(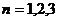 ,…) 9分
,…) 9分
所以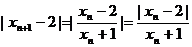 ≤
≤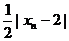 10分
10分
所以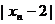 ≤
≤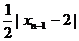 ≤
≤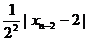 ≤…≤
≤…≤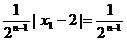 12分
12分
所以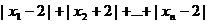 ≤
≤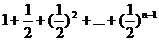
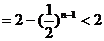 14分
14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com