
22.(2009-2010学年度扬州市第一学期期末高考模拟)已知函数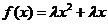 ,
,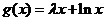 ,
,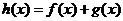 ,其中
,其中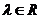 ,且
,且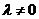 .⑴当
.⑴当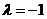 时,求函数
时,求函数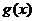 的最大值;⑵求函数
的最大值;⑵求函数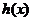 的单调区间;
的单调区间;
⑶设函数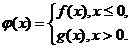 若对任意给定的非零实数
若对任意给定的非零实数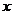 ,存在非零实数
,存在非零实数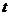 (
(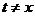 ),使得
),使得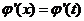 成立,求实数
成立,求实数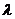 的取值范围.
的取值范围.
解:⑴当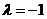 时,
时,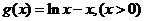 ∴
∴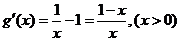
令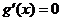 ,则
,则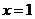 , ∴
, ∴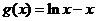 在
在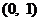 上单调递增,在
上单调递增,在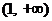 上单调递减
上单调递减
∴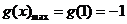 ----------------------------4分
----------------------------4分
⑵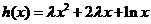 ,
,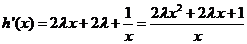 ,(
,(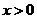 )
)
∴当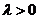 时,
时,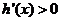 ,∴函数
,∴函数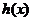 的增区间为
的增区间为 ,
,
当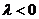 时,
时,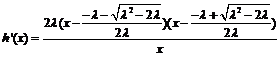 ,
,
当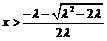 时,
时,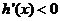 ,函数
,函数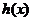 是减函数;
是减函数;
当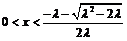 时,
时,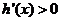 ,函数
,函数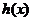 是增函数。
是增函数。
综上得,
当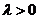 时,
时,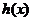 的增区间为
的增区间为 ;
;
当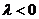 时,
时,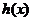 的增区间为
的增区间为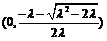 ,减区间为
,减区间为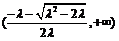 ----------10分
----------10分
⑶当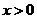 ,
,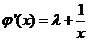 在
在 上是减函数,此时
上是减函数,此时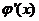 的取值集合
的取值集合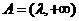 ;
;
当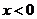 时,
时,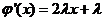 ,
,
若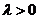 时,
时,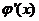 在
在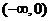 上是增函数,此时
上是增函数,此时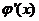 的取值集合
的取值集合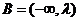 ;
;
若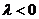 时,
时,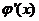 在
在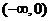 上是减函数,此时
上是减函数,此时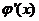 的取值集合
的取值集合 。
。
对任意给定的非零实数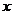 ,
,
①当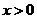 时,∵
时,∵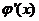 在
在 上是减函数,则在
上是减函数,则在 上不存在实数
上不存在实数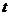 (
(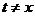 ),使得
),使得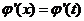 ,则
,则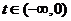 ,要在
,要在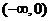 上存在非零实数
上存在非零实数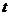 (
(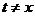 ),使得
),使得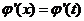 成立,必定有
成立,必定有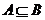 ,∴
,∴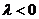 ;
;
②当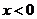 时,
时,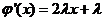 在
在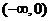 时是单调函数,则
时是单调函数,则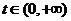 ,要在
,要在 上存在非零实数
上存在非零实数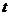 (
(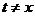 ),使得
),使得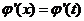 成立,必定有
成立,必定有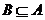 ,∴
,∴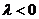 。
。
综上得,实数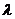 的取值范围为
的取值范围为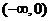 。
-------------------16分
。
-------------------16分
21.(绵阳市高中2010级第二次诊断性考试)设数列{an}的各项均为正数,它的前n项和为Sn(n∈N*),已知点(an,4Sn)在函数f (x)=x2+2x+1的图象上.
(1)证明{an}是等差数列,并求an;
(2)设m、k、p∈N*,m+p=2k,求证: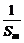 +
+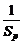 ≥
≥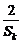 ;
;
(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由。www..co
解:(1)∵ 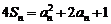 ,
,
∴ 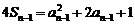 (n≥2).
(n≥2).
两式相减得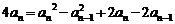 .
.
整理得
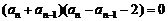 ,
,
∵ 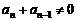 ,
,
∴ 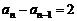 (常数).
(常数).
∴ {an}是以2为公差的等差数列.
又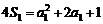 ,即
,即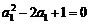 ,解得
,解得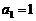 ,
,
∴ an=1+(n-1)×2=2n-1.………………………………………………………4分
(2)由(1)知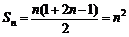 ,∴ Sm=m2,Sp=p2,Sk=k2.
,∴ Sm=m2,Sp=p2,Sk=k2.
由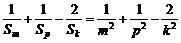
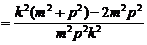
≥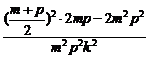 ≥
≥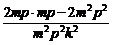 =0,
=0,
即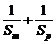 ≥
≥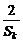 .………………………………………………………………7分
.………………………………………………………………7分
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则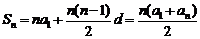 ,高@考#资$源@网
,高@考#资$源@网
∵ 
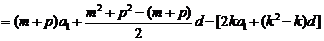 ,
,
把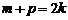 代入上式化简得
代入上式化简得

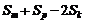 =
=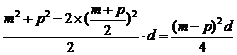 ≥0,
≥0,
∴ Sm+Sp≥2Sk.
又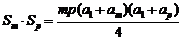 =
=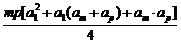
≤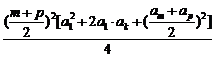
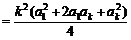
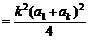
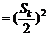 ,
,
∴ 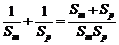 ≥
≥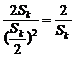 .
.
故原不等式得证.………………………………………………………………14分
20.(2010年浙江省杭州市第一次高考科目教学质量检测)已知函数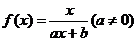 满足
满足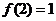 ,且方程f(x) = x有且仅有一个实数根.
,且方程f(x) = x有且仅有一个实数根.
(Ⅰ)求函数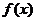 的解析式;
的解析式;
(Ⅱ)设数列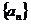 满足
满足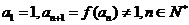 .求数列
.求数列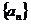 的通项公式;
的通项公式;
(Ⅲ)定义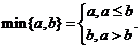 对于(Ⅱ)中的数列
对于(Ⅱ)中的数列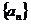 ,令
,令  设
设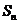 为数列
为数列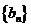 的前
的前 项和,求证:
项和,求证: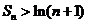 .
.
(Ⅰ)由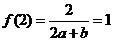 ,得
,得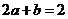 ;又
;又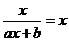 有且仅有一个解,即
有且仅有一个解,即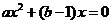 有唯一解满足
有唯一解满足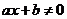 .
.
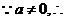 当
当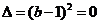 时,
时,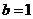 ,
,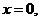 则
则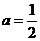 ,此时
,此时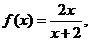
又当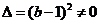 时,
时,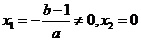 ,因为
,因为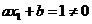 ,
,
所以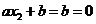 ,则
,则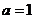 ,此时
,此时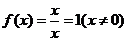
综上所述,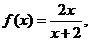 或者
或者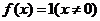 ;
4分
;
4分
(Ⅱ) 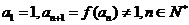 ,当
,当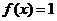 时,
时,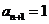 ,不合题意,
,不合题意,
则 ,
,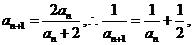 则
则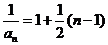 ,
,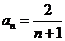 4分
4分
(Ⅲ)由(Ⅱ)知,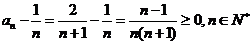
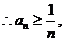 则
则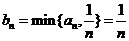 ,所以
,所以 2分
2分
设数列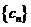 的前
的前 项和为
项和为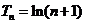 ,则
,则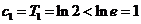
当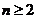 时,
时,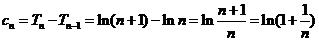 ,要证明
,要证明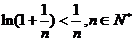
令 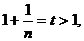 只要证明:
只要证明: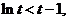 其中
其中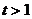 .
.
令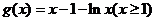 ,则
,则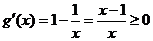 ,所以
,所以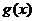 在
在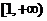 上是增函数,
上是增函数,
则当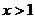 时,
时,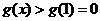 ,即
,即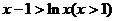 ,所以
,所以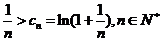 ,
,
则 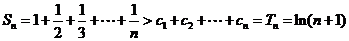 .
5分
.
5分
[说明]也可用数学归纳法证明,为此,先证明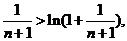 即证:
即证: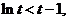 其中
其中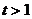 .
.
19.(宁波市2009学年度第一学期期末试卷)设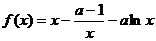
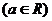 .
.
(1)若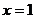 是函数
是函数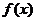 的极大值点,求
的极大值点,求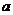 的取值范围;
的取值范围;
(2)当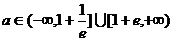 时,若在
时,若在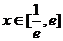 上至少存在一点
上至少存在一点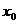 ,使
,使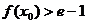 成立,求
成立,求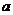 的取值范围.
的取值范围.
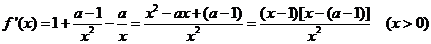
(2分)
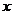 |
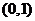 |
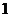 |
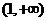 |
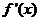 |
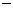 |
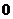 |
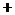 |
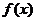 |
递减 |
极小值 |
递增 |
当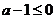 时,
时,
当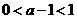 时,
时,
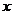 |
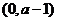 |
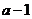 |
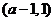 |
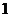 |
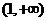 |
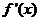 |
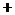 |
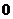 |
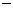 |
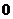 |
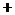 |
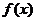 |
递增 |
极大值 |
递减 |
极小值 |
递增 |
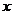 |
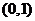 |
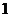 |
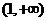 |
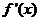 |
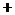 |
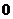 |
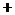 |
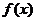 |
递增 |
非极值 |
递增 |
当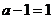 时,
时,
当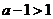 时,
时,
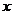 |
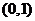 |
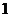 |
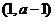 |
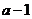 |
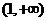 |
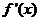 |
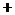 |
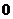 |
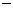 |
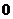 |
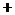 |
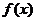 |
递增 |
极大值 |
递减 |
极小值 |
递增 |
综上所述,当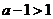 ,即
,即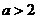 时,
时,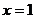 是函数
是函数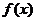 的极大值点. (7分)
的极大值点. (7分)
(2)在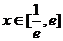 上至少存在一点
上至少存在一点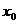 ,使
,使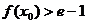 成立,等价于
成立,等价于
当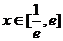 时,
时, 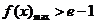 .
(9分)
.
(9分)
由(1)知,①当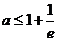 ,即
,即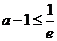 时,
时,
函数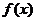 在
在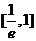 上递减,在
上递减,在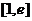 上递增,
上递增,
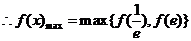 .
.
由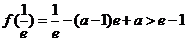 ,解得
,解得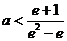 .
.
由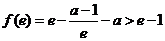 ,解得
,解得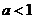
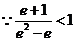 ,
, 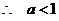 ; (12分)
; (12分)
②当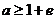 ,即
,即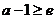 时,函数
时,函数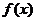 在
在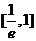 上递增,在
上递增,在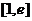 上递减,
上递减,
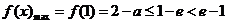 .
.
综上所述,当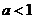 时,在
时,在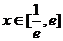 上至少存在一点
上至少存在一点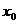 ,使
,使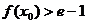 成立. (14分)
成立. (14分)
18.(江苏省南通市2009届高三上学期期末调研考试数学试卷)已知等差数列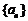 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列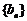 的首项为b,公比为a,其中a,b都是大于1
的首项为b,公比为a,其中a,b都是大于1
的正整数,且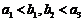 .(1)求a的值;
.(1)求a的值;
(2)若对于任意的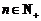 ,总存在
,总存在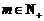 ,使得
,使得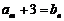 成立,求b的值;
成立,求b的值;
(3)令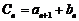 ,问数列
,问数列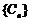 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
解:(1)由已知,得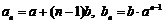 .由
.由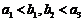 ,得
,得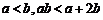 .
.
因a,b都为大于1的正整数,故a≥2.又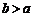 ,故b≥3.
……………………2分
,故b≥3.
……………………2分
再由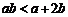 ,得
,得 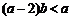 .
.
由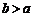 ,故
,故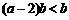 ,即
,即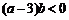 .
.
由b≥3,故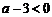 ,解得
,解得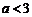 . …………………………………………………4分
. …………………………………………………4分
于是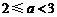 ,根据
,根据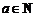 ,可得
,可得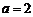 .……………………………………………6分
.……………………………………………6分
(2)由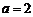 ,对于任意的
,对于任意的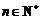 ,均存在
,均存在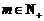 ,使得
,使得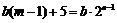 ,则
,则
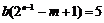 .
.
又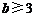 ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.
故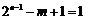 ,b=5.
,b=5.
所以b=5时,存在正自然数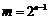 满足题意.………………………………………9分
满足题意.………………………………………9分
(3)设数列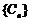 中,
中,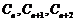 成等比数列,由
成等比数列,由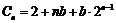 ,
,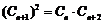 ,得
,得
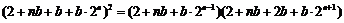 .
.
化简,得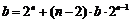 . (※) ……………………………………11分
. (※) ……………………………………11分
当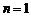 时,
时,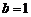
 时,等式(※)成立,而
时,等式(※)成立,而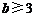 ,不成立.
……………………12分
,不成立.
……………………12分
当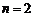 时,
时,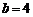 时,等式(※)成立.……………………………………………13分
时,等式(※)成立.……………………………………………13分
当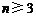 时,
时,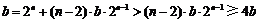 ,这与b≥3矛盾.
,这与b≥3矛盾.
这时等式(※)不成立.…………………………………………………………………14分
综上所述,当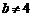 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当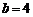 时,数列
时,数列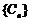 中的第二、三、四项成等比数列,这三项依次是18,30,50.……………………………………16分
中的第二、三、四项成等比数列,这三项依次是18,30,50.……………………………………16分
17.(湖北省部分重点中学2010届高三第二次联考)已知数列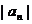 满足:
满足: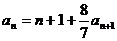 ,且存在大于1的整数k使
,且存在大于1的整数k使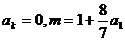 。
。
(1)用k表示m(化成最简形式); (2)若m是正整数,求k与m的值;
(3)当k大于7时,试比较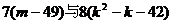 的大小。
的大小。
解:(1)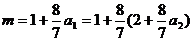
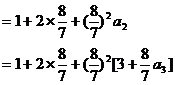
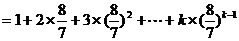 ① …………2分
① …………2分
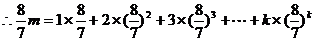 ②
②
由①-②得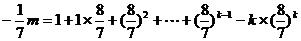 …………4分
…………4分
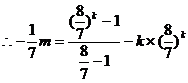
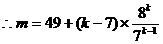 …………6分
…………6分
(2)由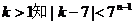
又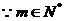 故此有
故此有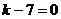
故k=7,m=49 …………9分
(3)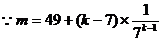
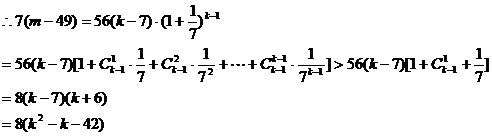
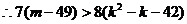 …………14分
…………14分
 w.k.s.5.u.c
w.k.s.5.u.c
16.(江苏省2010届苏北四市(徐州、宿迁、淮安、连云港)期末联考)已知函数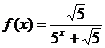 ,
,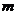 为正整数.
为正整数.
(Ⅰ)求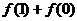 和
和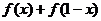 的值;
的值;
(Ⅱ)若数列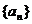 的通项公式为
的通项公式为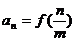 (
(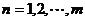 ),求数列
),求数列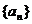 的前
的前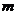 项和
项和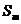 ;
;
(Ⅲ)设数列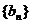 满足:
满足: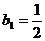 ,
,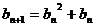 ,设
,设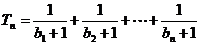 ,若(Ⅱ)中的
,若(Ⅱ)中的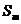 满足对任意不小于3的正整数n,
满足对任意不小于3的正整数n,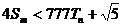 恒成立,试求m的最大值.
恒成立,试求m的最大值.
解:(Ⅰ)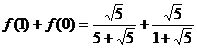 =1;
=1;
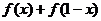 =
=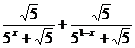 =
=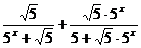 =1;…………4分
=1;…………4分
(Ⅱ)由(Ⅰ)得
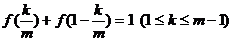 ,即
,即
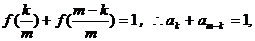
由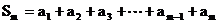 ,
……………①
,
……………①
得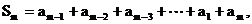 …………②
…………②
由①+②, 得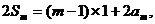
∴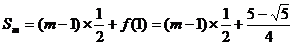 ,…10分
,…10分
(Ⅲ) ∵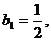
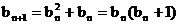 ,∴对任意的
,∴对任意的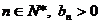 .
.
∴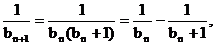 即
即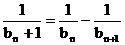 .
.
∴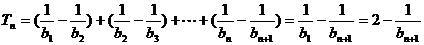 .
.
∵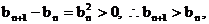 ∴数列
∴数列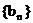 是单调递增数列.
是单调递增数列.
∴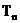 关于n递增. 当
关于n递增. 当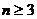 , 且
, 且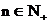 时,
时, 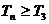 .
.
∵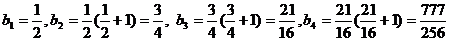
∴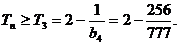 ∴
∴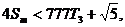 ∴
∴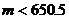 .而
.而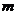 为正整数,
为正整数,
∴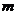 的最大值为650. ………………………………………………16分
的最大值为650. ………………………………………………16分
15.(武昌区2010届高三年级元月调研测试)设函数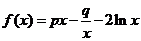 ,且
,且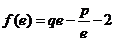 (
(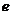 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求实数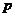 与
与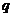 的关系;
的关系;
(Ⅱ)若函数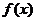 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数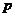 的取值范围;
的取值范围;
(Ⅲ)设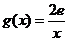 ,若存在
,若存在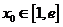 ,使得
,使得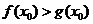 成立,求实数
成立,求实数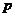 的取值范围.
的取值范围.
解:(Ⅰ)由题意,得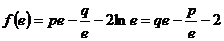 ,
,
化简,得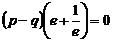 ,
,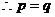 .
………………………………………………………………2分
.
………………………………………………………………2分
(Ⅱ)函数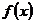 的定义域为
的定义域为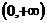 .由(Ⅰ)知,
.由(Ⅰ)知,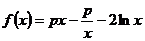 ,
,
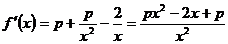 . ……………………………………………………………………3分
. ……………………………………………………………………3分
令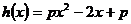 ,要使
,要使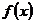 在其定义域
在其定义域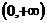 内为单调函数,只需
内为单调函数,只需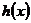 在
在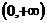 内满足
内满足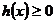 或
或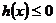 恒成立.
恒成立.
(1)当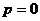 时,
时,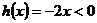 ,
,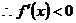 .
.
 在
在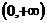 内为单调减函数,故
内为单调减函数,故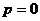 符合条件. …………………………………………………4分
符合条件. …………………………………………………4分
(2)当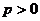 时,
时,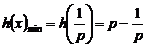 .只需
.只需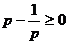 ,即
,即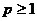 时
时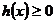 ,此时
,此时 .
.
 在
在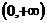 内为单调增函数,故
内为单调增函数,故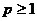 符合条件. ………………………………………………6分
符合条件. ………………………………………………6分
(3)当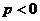 时,
时, .只需
.只需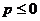 ,此时
,此时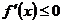 .
.
 在
在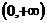 内为单调减函数,故
内为单调减函数,故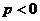 符合条件.
符合条件.
综上可得, 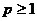 或
或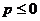 为所求.
………………………………………………………………………8分
为所求.
………………………………………………………………………8分
(Ⅲ)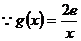 在
在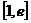 上是减函数,
上是减函数,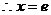 时,
时, ;
;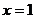 时,
时,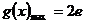 .
.
即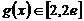 . ……………………………………………………………………………………………9分
. ……………………………………………………………………………………………9分
(1)当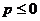 时,由(Ⅱ)知,
时,由(Ⅱ)知,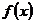 在
在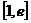 上递减,
上递减,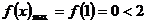 ,不合题意. ………10分
,不合题意. ………10分
(2)当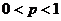 时,由
时,由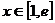 知,
知,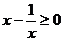 .
.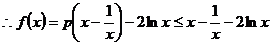 .
.
由(Ⅱ)知,当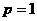 时,
时,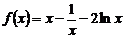 单调递增,
单调递增,
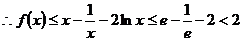 ,不合题意. …………………………………………………12分
,不合题意. …………………………………………………12分
(3)当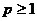 时,由(Ⅱ)知
时,由(Ⅱ)知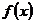 在
在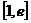 上递增,
上递增,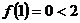 ,
,
又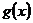 在在
在在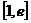 上递减,
上递减,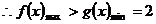 .
.
即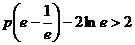 ,
,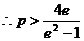 .
.
综上,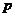 的取值范围是
的取值范围是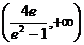 .…………………………………………………
.…………………………………………………
14.(昌平区2009-2010学年第一学期高三年级期末质量抽测)对于给定数列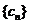 ,如果存在实常数
,如果存在实常数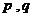 ,使得
,使得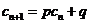 对于任意
对于任意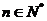 都成立,我们称数列
都成立,我们称数列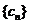 是 “M类数列”.
是 “M类数列”.
(I)若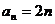 ,
,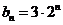 ,
,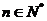 ,数列
,数列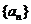 、
、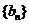 是否为“M类数列”?
是否为“M类数列”?
若是,指出它对应的实常数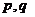 ,若不是,请说明理由;
,若不是,请说明理由;
(II)若数列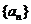 满足
满足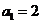 ,
,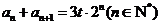 ,
,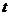 为常数.
为常数.
(1)
求数列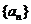 前
前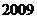 项的和;
项的和;
(2)
是否存在实数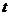 ,使得数列
,使得数列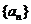 是“M类数列”,如果存在,求出
是“M类数列”,如果存在,求出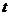 ;如果不存在,说明理由.
;如果不存在,说明理由.
解:(I)因为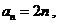 则有
则有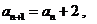
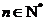
故数列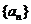 是“M类数列”, 对应的实常数分别为
是“M类数列”, 对应的实常数分别为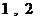 . ……………………………2分
. ……………………………2分
因为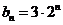 ,则有
,则有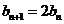
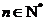
故数列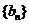 是“M类数列”, 对应的实常数分别为
是“M类数列”, 对应的实常数分别为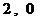 . ……………………………4分
. ……………………………4分
(II)(1)因为 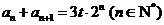 则有
则有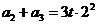 ,
,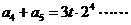 ,
,
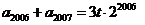 ,
, 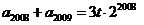 ……………………………….6分
……………………………….6分
故数列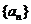 前
前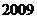 项的和
项的和
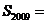
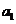 +
+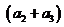 +
+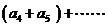 +
+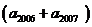 +
+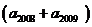
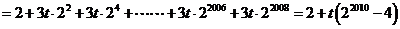 ………………9分
………………9分
若数列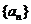 是“M类数列”, 则存在实常数
是“M类数列”, 则存在实常数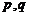
使得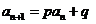 对于任意
对于任意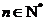 都成立,………………………………………….10分
都成立,………………………………………….10分
且有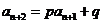 对于任意
对于任意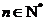 都成立,
都成立,
因此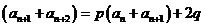 对于任意
对于任意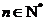 都成立,
都成立,
而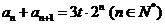 ,且
,且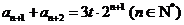
则有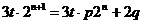 对于任意
对于任意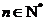 都成立,可以得到
都成立,可以得到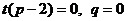 ,………………………………………12分
,………………………………………12分
①当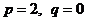 时,
时,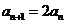 ,
,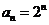 ,
,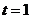 ,经检验满足条件.
,经检验满足条件.
②当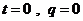 时,
时,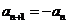 ,
,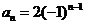 ,
,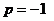 经检验满足条件.
经检验满足条件.
因此当且仅当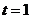 或
或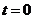 ,时,数列
,时,数列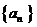 也是“M类数列”.对应的实常数分别为
也是“M类数列”.对应的实常数分别为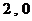 , 或
, 或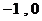 .
………………………………………………………………14分
.
………………………………………………………………14分
2.当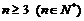 时,证明:
时,证明: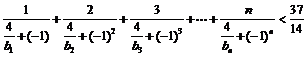 .
.
证明:(1) 由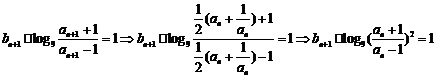
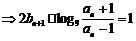 又
又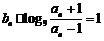 ∴
∴ 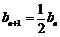
又n = 1时,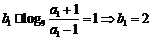
∴ 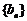 为等比数列,b1 = 2,
为等比数列,b1 = 2,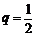 ,∴
,∴ 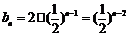
(2) ∵ 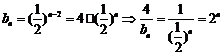 ∴
∴ 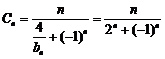
先证: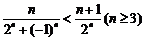
当n为偶数时,显然成立;
当n为奇数时,即证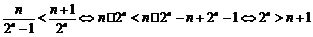
而当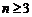 时,
时,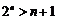 显然也成立,故
显然也成立,故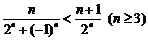
当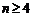 时,令
时,令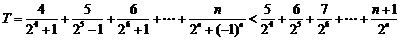
又令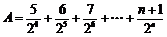 ①
①
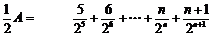 ②
②
①-②: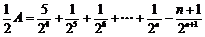
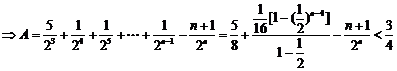
∴ 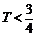
又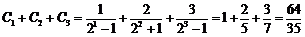
∴ 所证式子左边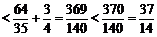
即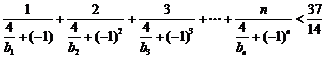
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com