
(1)设集合A = {x|x2-1>0}, B= {x|log2x>0}, 则A∩B等于
(A){x|x>1} (B) {x|x>0} (C){x|x<-1} (D) {x|x<-1或x>1}
(2)若(x2-1)+(x2-2x-3)i是纯虚数,则实数x的值是
(A)1 B) -1 (C) ±1 (D) 以上都不对
(3)已知等差数列{an}的各项均为正,且公差不为0,设P= ,Q=
,Q= ,则P与Q的大小关系为
,则P与Q的大小关系为
(A) P>Q (B) P<Q (C) P=Q (D) 无法确定
(4)已知sin( +
+ )=
)= 且tan
且tan <0则cos
<0则cos 的值为
的值为
(A)  (B)
(B)
 (C)
(C)  (D)
(D) 
(5)直线l1,l2互相平行的一个充分条件是
(A) l1,l2都平行于平面 (B)
l1,l2与平面
(B)
l1,l2与平面 所成的角相等
所成的角相等
(C) l1平行于l2所在平面 (D) l1,l2都垂直于平面
(D) l1,l2都垂直于平面
(6)平面上有四个互异的点A、B、C、D,满足( -
- )·(
)·( -
- )=0,则三角形ABC是
)=0,则三角形ABC是
(A) 直角三角形 (B) 等腰三角形
(C) 等腰直角三角形 (D) 等边三角形
(7)将一张坐标纸折叠一次,使点(10,0)与(-6,8)重合,则与点(-4,2)重合的点是
(A) (4,-2) (B) (4,-3) (C) (3,  ) (D) (3,-1)
) (D) (3,-1)
(8)对一组数据Zi(i=1,2,3,…,n),如果将它们改变为Zi-C(i=1,2,3,…,n),其中C≠0,则下面结论正确的是
(A) 平均数与方差均不变 (B) 平均数变了,而方差保持不变
(C) 平均数不变,方差变了 (D) 平均数与方差均发生了变化
(9)正方体的八个顶点中有四个恰为正四面体的顶点,则正方体的全面积与正四面体的全面积之比为
(A)  (B)
(B)  (C)
(C)
 (D)
(D)

(10)F1、F2是双曲线
 =1的左、右两个焦点,P是双曲线右支上任一点,从右焦点向∠F1PF2的平分线作垂线,垂足为M,点M的轨迹是曲线C的一部分,则曲线C是
=1的左、右两个焦点,P是双曲线右支上任一点,从右焦点向∠F1PF2的平分线作垂线,垂足为M,点M的轨迹是曲线C的一部分,则曲线C是
(A) 圆 (B) 椭圆 (C) 双曲线 (D) 抛物线
(11)已知函数f(x)=
 +m+1对x∈(0,
+m+1对x∈(0, )的图象恒在x轴上方,则m的取值范围是
)的图象恒在x轴上方,则m的取值范围是
(A) 2-2 <m<2+2
<m<2+2 (B) m<2
(B) m<2
(C) m<2+2 (D) m≥2+2
(D) m≥2+2
(12)a1、b1、c1、a2、b2、c2均为非零实数,不等式a1x2+b1x+c1>0和a2x2+b2x+c2>0的解集分别为集合M和N,那么“ ”是“M=N”的
”是“M=N”的
(A)充分非必要条件. (B)必要非充分条件.
(C)充要条件 (D)既非充分又非必要条件.
(17) ( 本题满分12分 )
已知函数
(I)求的最小正周期;
(II)若,求的最大值,最小值.
(18) ( 本题满分12分 )
已知一台机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作.一周五天工作日里无故障可获利10万元,发生一次故障可获利5万元,发生两次故障没有利润,发生三次或三次以上故障就要亏损2万元.这台机器在一周内平均获利多少?
(19) ( 本题满分12分 )
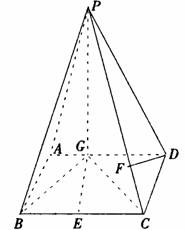 已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG=
已知,如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABCD,垂足为G,G在AD上,且AG= GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为
GD,BG⊥GC,GB=GC=2,E是BC的中点,四面体P-BCG的体积为 .
.
(Ⅰ)求异面直线GE与PC所成的角;
(Ⅱ)求点D到平面PBG的距离;
(Ⅲ)若F点是棱PC上一点,且DF⊥GC,求 的值.
的值.
(20) ( 本题满分12分 )
已知等差数列 的前n 项之和为Sn,令
的前n 项之和为Sn,令 ,且
,且 ,S6-S3=15.
,S6-S3=15.
(Ⅰ)求数列 的通项公式与它的前10项之和;
的通项公式与它的前10项之和;
(Ⅱ)若 ,
, ,
, =
= ,求
,求 的值.
的值.
(21) ( 本题满分12分 )
已知点 ,动点
,动点 、
、 分别在
分别在 、
、 轴上运动,满足
轴上运动,满足 ,
, 为动点,并且满足
为动点,并且满足 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过点 的直线
的直线 (不与
(不与 轴垂直)与曲线
轴垂直)与曲线 交于
交于 两点,设点
两点,设点  ,
, 与
与 的夹角为
的夹角为 ,求证:
,求证: .
.
(22) ( 本题满分14分 )
函数 的定义域为R,且
的定义域为R,且
(Ⅰ)求证: ;
;
(Ⅱ)若 上的最小值为
上的最小值为 ,试求f(x)的解析式;
,试求f(x)的解析式;
(Ⅲ)在(Ⅱ)的条件下记 试比较
试比较 与
与
 的大小并证明你的结论.
的大小并证明你的结论.
(13)已知点P在抛物线 上运动,定点A(0,-1),若点M分
上运动,定点A(0,-1),若点M分 所成的比为2,则动点M的轨迹方程是
.
所成的比为2,则动点M的轨迹方程是
.
(14) 一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,测的刹车后 秒内列车前进的距离为
秒内列车前进的距离为 米,则列车刹车后
秒车停下来,期间列车前进了
米.
米,则列车刹车后
秒车停下来,期间列车前进了
米.
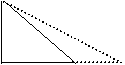 (15)在测量学中,把斜坡的坡面与水平面所成二
(15)在测量学中,把斜坡的坡面与水平面所成二
面角的大小叫做坡角.若要将坡长为100 m 、 100 m
坡角为450的坡面,改造成坡角为300的坡面, 450 300
则坡底要伸长 m.
(16) 设有两个命题: ① 不等式 + 4 >m> 2x-x2对一切实数x恒成立;
+ 4 >m> 2x-x2对一切实数x恒成立;
② 函数f(x)=- 是R上的减函数.
是R上的减函数.
使这两个命题都是真命题的充要条件,用m可表示为 .
(1)计算: ( )
( )
(A)2 (B) (C)
(C) (D)
(D)
(2)已知 ,则
,则 在
在 上的射影为
上的射影为
(A)  ; (B)
; (B)  ; (C)
; (C)  ; (D)
; (D) 

(3)已知a、b为直线,α、β为平面.在下列四个命题中,
① 若a⊥α,b⊥α,则a∥b ; ② 若 a∥α,b ∥α,则a∥b;
③ 若a⊥α,a⊥β,则α∥β; ④ 若α∥b,β∥b ,则α∥β.
正确命题的个数是
(A) 1 (B) 3 (C) 2 (D) 0
(4)函数f(x)=A·tan(ωx+φ)(φ>0)在区间[m,n]上的函数值都小于0,则函数g(x)=A·cot(ωx+φ)在[m,n]上的函数值
(A) 都大于0,且有最大值为g(m) (B) 都小于0,且有最大值为g(m)
(C) 都大于0,且有最小值为g(m) (D) 都小于0,且有最小值为g(m)
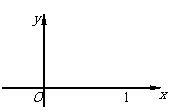 (5)已知函数
(5)已知函数 的图象的一段圆弧(如图所示)
的图象的一段圆弧(如图所示)
若 ,则
,则
 (A)
(A) (B)
(B)
(C) (D)前三个判断都不正确
(D)前三个判断都不正确
(6)对于四条曲线:①  ;②
;②  ;③
;③  ;
;
④  . 其中与直线2 x + y +3=0有交点的所有曲线是
. 其中与直线2 x + y +3=0有交点的所有曲线是
(A) ②,③,④ (B) ①,② (C) ②,④ (D) ①,②,③
(7)将4名司机和8名售票员分配到四辆公共汽车上,每辆车上分别有1名司机和2名售票员,则可能的分配方案种数是
(A) (B)
(B) (C)
(C) (D)
(D)
(8)定义在R上的偶函数f(x)在 上递增,
上递增, ,则满足
,则满足 >0的x的取值范围是
>0的x的取值范围是
(A) (B)
(B) (C)
(C)  (D)
(D) 
(9)现有一个长方体水箱,从水箱里面量得它的深是30cm,底面的长是25cm,宽是20cm.设0< a ≤8,水箱里盛有深为a cm的水,若往水箱里放入棱长为10cm的立方体铁块,则水深为
(A) 2 cm
(B) 10 cm
(C) (a+2) cm
(D) 
(10)我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F为一个焦点的椭圆,近地点A距地面为m公里,远地点B距地面为n公里.若地球的半径为R公里,则飞船运行轨道的短轴长为
(A) mn (B) 2 (C) 2nm (D)
(C) 2nm (D) 
(11)已知函数f(x)的图象过点(0,-5),它的导数f /(x)=4x3-4x,则当f(x)取得最大值-5时,x的值应为
(A) -1 (B) 0 (C) 1 (D) ±1
(12)在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
(A) (B)
(B) (C)
(C) (D)
(D) 
(17)(本题满分8分)
已知 是第二象限角,且
是第二象限角,且 ,求
,求 的值.
的值.
(18)(本题满分10分)
已知
(I)若 时,
时, 最大值为4,求
最大值为4,求 的值
的值
(II)在(I)的条件下,求满足 且
且 的
的 的集合
的集合
(19)(本题满分10分)
在 中,
中, ,求
,求 的值和
的值和 的面积
的面积
(20)(本题满分12分)已知 ,
, ,
, 与
与 的夹角为
的夹角为 ,
, 与
与 的夹角为
的夹角为 ,且
,且 ,求
,求 的值。
的值。
(13) =
.
=
.
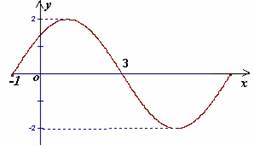 (14)已知
(14)已知 ,
, 的图象如图所示,则它的解析式为 _____
.
的图象如图所示,则它的解析式为 _____
.
(15)已知函数 则它的单调递减区间为
.
则它的单调递减区间为
.
(16)函数 的值域为
.
的值域为
.
(1)如果角2α的终边在x轴上方,那么α的范围是
(A) 第一象限角的集合 (B) 第一或第二象限角的集合
(C) 第一或第三象限角的集合 (D) 第一或第四象限角的集合
(2)若 是周期为
是周期为 的奇函数,则
的奇函数,则 可以是
可以是
(A)
 (B)
(B)
 (C)
(C)
 (D)
(D)

(3))函数 的图像的一条对称轴是
的图像的一条对称轴是
(A) (B)
(B)
 (C)
(C)  (D)
(D) 
(4)设 ,若
,若 ,则
,则
(A) (B)
(B) (C)
(C) (D)
(D)
(5)( )可化简为
)可化简为
(A) 2 (B)2
(C)
(B)2
(C)  (D)
(D) 
(6)在 中,“
中,“ ”是“
”是“ ”的
”的
(A)充分而不必要条件 (B) 必要而不充分条件
(C)充分必要条件 (D) 既不充分也不必要条件
(7)已知点P( ,
, )在第一象限,则在[0,2π)内α的取值范围是
)在第一象限,则在[0,2π)内α的取值范围是
(A)( ,
, )∪
)∪ (B)
(B)  ∪
∪
(C)  ∪
∪ (D)
(D)  ∪
∪
(8) 把函数 的图像向左平移
的图像向左平移 (
(
 个单位,所得图像关于
个单位,所得图像关于 轴对称,则
轴对称,则 的最小值是
的最小值是
(A) (B)
(B)
 (C)
(C)
 (D)
(D) 
(9)将函数 按向量
按向量 平移,得到函数
平移,得到函数 的图象,那么
的图象,那么 可以是
可以是
(A) (B)
(B) (C)
(C) (D)
(D)
(10)函数 的定义域是
的定义域是
(A) (B)
(B) 
(C)  (D)
(D)

(11)在△ABC中, 分别为角
分别为角 的对边,若
的对边,若 成等差数列,
成等差数列, ,
, 的面积为
的面积为 ,则
,则
(A) (B)
(B) (C)
(C) (D)
(D)
(12)定义在 上的函数
上的函数 既是偶函数,又是周期函数,若
既是偶函数,又是周期函数,若 的最小正周期是
的最小正周期是 ,且当
,且当 时,
时, ,则
,则 的值为
的值为
(A) (B)
(B) (C)
(C) (D)
(D)
 (18).设中心为O,正西的观测点为A,正东的观测点为B,正北的观测点为C,以O为原点建立直角坐标系,由已知巨响的位置M在AC的中垂线上,且在以A、B为焦点,实轴为1360的双曲线左支上,AC的中垂线:
(18).设中心为O,正西的观测点为A,正东的观测点为B,正北的观测点为C,以O为原点建立直角坐标系,由已知巨响的位置M在AC的中垂线上,且在以A、B为焦点,实轴为1360的双曲线左支上,AC的中垂线: ① 双曲线:
① 双曲线: ②
②
解①②得 ∴巨响位于西北方向,距中心为68m。
∴巨响位于西北方向,距中心为68m。
(19) 解(I)设 过顶点E(-1,0),则
过顶点E(-1,0),则
 由E、A、B三点共线,知
由E、A、B三点共线,知 //
// , 所以,
, 所以, 即
即 ,因为
,因为 ,所以
,所以
所以 (与
(与 无关).
无关).
(II)设 ,则由
,则由 ,
,
 即
即 又
又 所以点
所以点 的轨迹方程为
的轨迹方程为 .
.
解法二提示:设 ,则
,则 联立方程组
联立方程组
 由韦达定理得
由韦达定理得
 可解得
可解得
(20) (I)由题意得:

(II)由 得
得 ,
,
由于直线与椭圆有两个不同的交点, ,即
,即 ①
①
(1)当 时,设弦MN的中点为
时,设弦MN的中点为 分别为点M、N的横坐标,则
分别为点M、N的横坐标,则

又 ②,将②代入①得
②,将②代入①得 ,解得
,解得 , 由②得
, 由②得 , 故所求的
, 故所求的 取值范围是
取值范围是 .
.
(2)当 时,
时, .
.

(13)  (14) 2 (15)
(14) 2 (15)  (16)
(16) 
(1)A (2)B (3)A (4)A (5)C (6)D (7)C (8)B (9)C (10)B (11)D (12)D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com