
21.(本题14分)已知数列 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程
 N
N 的两根,且
的两根,且 .
.
(I)求证: 数列 是等比数列;
是等比数列;
(II)设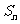 是数列
是数列 的前
的前 项和,求
项和,求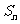 .
.
(III)问是否存在常数 ,使得
,使得 对任意
对任意 N
N 都成立,若存在,求出
都成立,若存在,求出 的取值范围; 若不存在
的取值范围; 若不存在 ,请说明理由.
,请说明理由.
 四市九校2010届高三第一次联考试
四市九校2010届高三第一次联考试
数 学(理)
|
学 校 |
|
|
|
班 级 |
|
|
|
考 号 |
|
|
|
姓 名 |
|
|
20.(本题13分)2008年世界经济出现严重衰退,我国政府为了刺激经济增长,2009年开始加大货币贷款量,为一批中小企业解决资经短缺问题.某私营企业获得一笔贷款准备新建一栋面积为10000m2,高为10m,底面为矩形的厂房,由于受地理环境的影响,矩形的一边(南北方向)不能超过a(m),已知厂房的地面造价为800元/m2,顶的造价为500元/m2,墙壁的造价为600元/m2,设厂房南北方向长为x(m),造价为y(元).
(I)写出用x(m)表示y(元)的函数关系式并指出定义域;
(II)求x为何值时厂房的造价最低,并求出最低价.

19.(本题12分)已知函数
(I)当 的单调区间;
的单调区间;
(II)是否存在实数a,使f(x)的极大值为3?若存在,求出a的值,若不存在,请说明理由.
18.(本题12分)已知:函数 的周期为3
的周期为3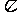 ,且当
,且当 时,函数
时,函数 的最小值为0.
的最小值为0.
(I)求函数 的表达式;
的表达式;
(II)在△ABC中,若 ,且2sin2B=cosB+cos
,且2sin2B=cosB+cos (A-C
(A-C ),求
),求 的值.
的值.
17.(本题12分)设向量
 ,其中
,其中 .
.
(I)求 的取值范围;
的取值范围;
(II)若函数 的大小.
的大小.

16.(本题12分)记关于 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为 .
.
(I)求 ;
;
(II)若 ,求实数
,求实数 的取值范围.
的取值范围.
15.代号为“狂飙”的台风于某日晚8点在距港口的A码头南偏东60°的400千米的海面上形成,预计台风中心将以40千米/时的速度向正北方向移动,离台风中心350千米的范围都会受到台风影响,则A码头从受到台风影响到影响结束,将持续多少小时 ★ .
14.已知点 是边长为
是边长为 的等边三角形内一点,它到三边的距离分别为
的等边三角形内一点,它到三边的距离分别为 、
、 、
、 ,则
,则 、
、 、
、 所满足的关系式为 ★ ,
所满足的关系式为 ★ , 的最小值是 ★ .
的最小值是 ★ .
12.给出下列类比推理:
①“若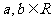 ,则
,则 ”类比推出“若
”类比推出“若 ,则
,则 ”;
”;
②“若 ,则复数
,则复数 ”类比推出
”类比推出
“若 ,则
,则 ”;
”;
③“若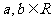 ,则
,则 ”类比推出“若
”类比推出“若 ,则
,则 ”;
”;
④“若 ,则
,则 ”类比推出“若
”类比推出“若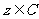 ,则
,则 ”.
”.
其中类比结论正确有 ★ .
1 3.点P(x,y)满足
3.点P(x,y)满足 ,点A的坐标是(1,2)
,点A的坐标是(1,2) ,若∠AOP=
,若∠AOP= ,
,
则︱ ︱cos
︱cos 的最大值是 ★ .
的最大值是 ★ .
11.定义在 上的函数
上的函数 是奇函数又是以
是奇函数又是以 为周期的周期函数,则f(1)+f(4)+f(7)等于 ★ .
为周期的周期函数,则f(1)+f(4)+f(7)等于 ★ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com