21．(本题14分)已知．

(I)若函数在区间上是增函数，在区间上是减函数，又，求的解析式；

(II)当，为非零实数时，证明的图象不存在与直线平行的切线；

(III)在(I)条件下，若在区间上恒有≤成立，求实数的取值范围．

四市九校2010届高三第一次联考试

数　 学(文)

20．(本题13分)已知函数的图象过点，．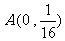

(I)求函数的表达式；

(II)设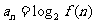，，是数列的前n项和，求；

(III)在(II)的条件下，若，求数列的前n项和．

19．(本题12分)长沙市将河西作为环境友好型和资源节约型的两型社会先导区，为加强先导区的建设，要改造枫林路，如图所示，规划沿路修建圆形休闲广场，圆心为O，半径为100米，其与枫林路一边所在的直线l相切于M点，A为上半圆弧上一点．过点A作l的垂线，垂足为B，市园林局计划在△ABM内进行绿化，设△ABM的面积为S(单位：平方米)．

(I)以∠AON=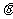(rad)为参数，将S表示成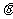的函数；

(II)为使绿化的面积最大，试确定此时点A的位置及其最大的面积．

18．(本题12分)设P表示幂函数在(0，+∞)上是增函数的c的集合；Q表示不等式≥c对任意恒成立的c的集合．

(I)写出；

(II)试写出一个解集为的不等式．

17．(本题12分)已知平面向量，．

(I)若存在实数k和t，使得，，且，试求函数的关系式k=f(t)；

(II)根据(I)结论，确定k=f(t)的单调区间．

16．(本题12分)设函数．其中为常数，且．

(I)求函数的最小正周期T；

(II)若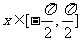时，的最大值为1，求的值．

15． 定义在R上的函数是奇函数，且，在区间[1，2]上是单调递减函数． 关于函数有下列结论：

①图象关于直线x=1对称；　　　　　　　 ②最小正周期是2；

③在区间[2，1]上是减函数；　　　 ④在区间[4，4]上的零点最多有5个．

其中正确的结论序号是　 ★　 ．(把所有正确结论的序号都填上)

14．已知，［x］表示不大于x的最大整数，如，，，则　 ★　 ；使成立的x的取值范围是　 ★　 ．

13．　 ★　 ．

12． 是奇函数，

它们的定义域均为，且它们在上的

图象如图所示，则不等式　 ★　 ．