
20. (本小题共14分)
已知函数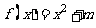 ,其中
,其中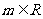 .定义数列
.定义数列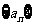 如下:
如下: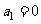 ,
, .
.
(I)当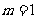 时,求
时,求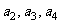 的值;
的值;
(II)是否存在实数m,使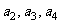 构成公差不为0的等差数列?若存在,请求出实数
构成公差不为0的等差数列?若存在,请求出实数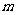 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(III)求证:当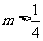 时,总能找到
时,总能找到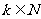 ,使得
,使得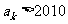 .
.
海淀区高三年级第一学期期末练习
19. (本小题共14分)
已知圆C经过点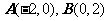 ,且圆心在直线
,且圆心在直线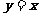 上,且,又直线
上,且,又直线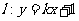 与圆C相交于
与圆C相交于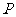 、
、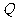 两点.
两点.
(I)求圆C的方程;
(II)若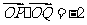 ,求实数
,求实数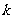 的值;
的值;
(III)过点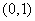 作直线
作直线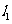 与
与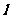 垂直,且直线
垂直,且直线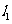 与圆C交于
与圆C交于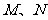 两点,求四边形
两点,求四边形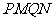 面积的最大值.
面积的最大值.
18. (本小题共13分)
函数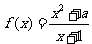
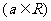 .
.
(I)若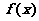 在点
在点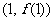 处的切线斜率为
处的切线斜率为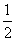 ,求实数
,求实数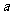 的值;
的值;
(II)若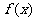 在
在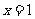 处取得极值,求函数
处取得极值,求函数 的单调区间.
的单调区间.
17. (本小题共14分)
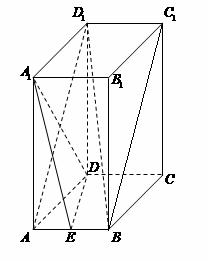 长方体
长方体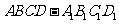 中
中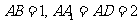 .
.
点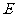 为AB中点.
为AB中点.
(I)求三棱锥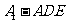 的体积;
的体积;
(II)求证: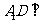 平面
平面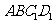 ;
;
(III)求证: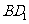
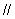 平面
平面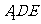 .
.
16. (本小题共13分)
(本小题共13分)
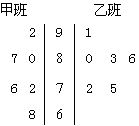
某校高三年级进行了一次数学测验,随机从甲乙两班各抽取6名同学,所得分数的茎叶图如右图所示:
(I)根据茎叶图判断哪个班的平均分数较高,并说明理由;
(II)现从甲班这6名同学中随机抽取两名同学,求他们的分数之和大于165分的概率.
15. (本小题共12分)
已知集合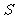 ={
={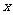 |
|
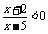 },
},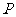 ={
={ 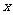 |
| 
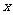
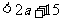 },
},
(Ⅰ)求集合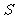 ;
;
(Ⅱ)若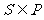 ,求实数a的取值范围.
,求实数a的取值范围.
14.对于函数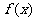 ,若存在区间
,若存在区间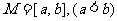 ,使得
,使得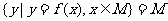 ,则称区间
,则称区间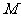 为函数
为函数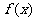 的一个“稳定区间”.
的一个“稳定区间”.
请你写出一个具有“稳定区间”的函数__________;(只要写出一个即可)
给出下列4个函数:
①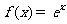 ;②
;②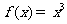 ,③
,③ ④
④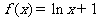
其中存在“稳定区间”的函数有_______(填上正确的序号)
13.已知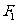 为椭圆
为椭圆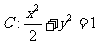 的左焦点,直线
的左焦点,直线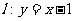 与椭圆
与椭圆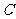 交于
交于 两点,那么
两点,那么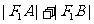 的值为_______.
的值为_______.
12.在区间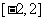 上,随机地取一个数
上,随机地取一个数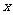 ,则
,则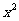 位于0到1之间的概率是____________.
位于0到1之间的概率是____________.
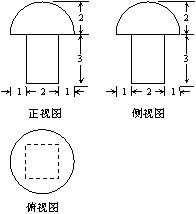
11.一个几何体的三视图如图所示,则该几何体的表面积为__________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com