
20. (本题满分16分)
已知数列 是公差为
是公差为
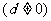 的等差数列,
的等差数列,
数列 是公比为
是公比为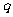 的(q∈R)的等比数列,若函数
的(q∈R)的等比数列,若函数 ,且
,且
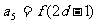 ,
, ,
, ,
,
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,对一切
,对一切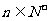 ,都有
,都有 成立,求
成立,求
19.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知函数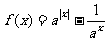 (其中
(其中 且
且 ,
,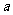 为实数常数).
为实数常数).
(1)若 ,求
,求 的值(用
的值(用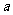 表示);
表示);
(2)若 且
且 对于
对于 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用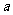 表示).
表示).
18.(本题满分15分)由于卫生的要求游泳池要经常换水(进一些干净的水同时放掉一些脏水), 游泳池的水深经常变化,已知泰州某浴场的水深 (米)是时间
(米)是时间 ,(单位小时)的函数,记作
,(单位小时)的函数,记作 ,下表是某日各时的水深数据
,下表是某日各时的水深数据
|
t(时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y(米) |
2 5
5 |
2 0
0 |
1 5 5 |
2 0 0 |
2 49 49 |
2 |
1 51 51 |
1 99 99 |
2 5
5 |
经长期观测的曲线 可近似地看成函数
可近似地看成函数
(Ⅰ)根据以上数据,求出函数 的最小正周期T,振幅A及函数表达式;
的最小正周期T,振幅A及函数表达式;
(Ⅱ)依据规定,当水深大于2米时才对游泳爱好者开放,请依据(1)的结论,
判断一天内的上午8 00至晚上20
00至晚上20 00之间,有多少时间可供游泳爱好者进行运动
00之间,有多少时间可供游泳爱好者进行运动
17.(本题满分15分)已知动点 到点
到点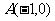 的距离是它到点
的距离是它到点 的距离的
的距离的 倍.
倍.
(Ⅰ) 试求点 的轨迹方程;
的轨迹方程;
(Ⅱ) 试用你探究到的结果求 面积的最大值.
面积的最大值.
16. (本题满分14分)四棱锥
(本题满分14分)四棱锥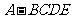 中,底面
中,底面 为矩形,
为矩形,
侧面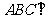 底面
底面 ,
,
 .
.
(Ⅰ)取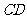 的中点为
的中点为 ,
, 的中点为
的中点为 ,证明:
,证明: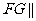 面
面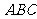 ;
;
(Ⅱ)证明: .
.
15.(本题满分14分)
设 的内角
的内角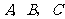 所对的边长分别为
所对的边长分别为 ,且
,且 ,
, .
.
(Ⅰ)求 和边长
和边长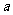 ;
;
(Ⅱ)若 的面积
的面积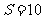 ,求
,求 的值.
的值.
14.对于任意实数 ,符号[
,符号[ ]表示
]表示 的整数部分,即[
的整数部分,即[ ]是不超过
]是不超过 的最大整数”。在实数轴R(箭头向右)上[
的最大整数”。在实数轴R(箭头向右)上[ ]是在点
]是在点 左侧的第一个整数点,当
左侧的第一个整数点,当 是整数时[
是整数时[ ]就是
]就是 。这个函数[
。这个函数[ ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
那么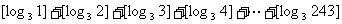 = .
= .
13.已知正四棱锥P-ABCD的高为4,侧棱长与底面所成的角为 ,
,
则该正四棱锥的侧面积是 .
12.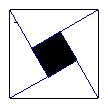 如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角
如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是___
.
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是___
.
11.在平面直角坐标系中,点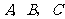 的坐标分别为
的坐标分别为 .
.
如果 是
是 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当 取到最大值时,
取到最大值时,
点 的坐标是 .
的坐标是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com