
8.(2009-2010学年度淄博市重点高中高三阶段考理科数学)已知数列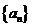 的前n项和
的前n项和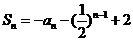 (n为正整数)。
(n为正整数)。
(Ⅰ)令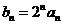 ,求证数列
,求证数列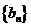 是等差数列,并求数列
是等差数列,并求数列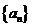 的通项公式;
的通项公式;
(Ⅱ)令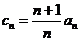 ,
,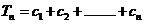 比较
比较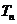 与
与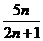 的大小,并证明。(本小题满分14分)
的大小,并证明。(本小题满分14分)
解:(I)在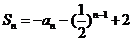 中,令n=1,可得
中,令n=1,可得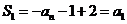 ,即
,即
当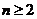 时,
时,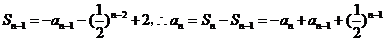 ,…… 2分
,…… 2分

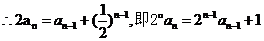 .
.
 .
.
.
.
又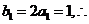 数列
数列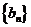 是首项和公差均为1的等差数列. ……………………4分
是首项和公差均为1的等差数列. ……………………4分
于是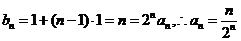 .……………………5分
.……………………5分
(II)由(I)得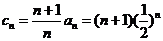 ,所以
,所以
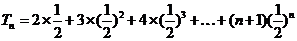
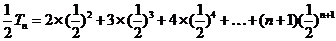
由①-②得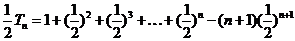
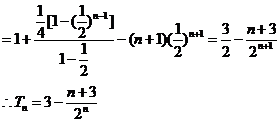
……………………8分
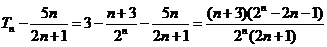
于是确定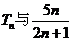 的大小关系等价于比较
的大小关系等价于比较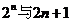 的大小
的大小
由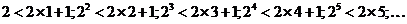
可猜想当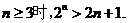 证明如下:……………………10分
证明如下:……………………10分
证法1:(1)当n=3时,由上验算显示成立。
(2)假设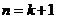 时
时
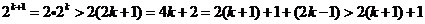
所以当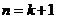 时猜想也成立
时猜想也成立
综合(1)(2)可知
,对一切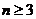 的正整数,都有
的正整数,都有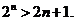
证法2:当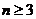 时
时
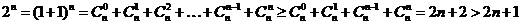
综上所述,当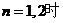
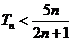 ,当
,当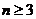 时
时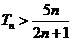
7.(山东省威海市2010届高三上学期教学质量检测)
已知函数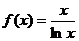 .(Ⅰ)求函数
.(Ⅰ)求函数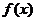 的单调减区间和极值;
的单调减区间和极值;
(Ⅱ)当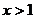 时,若
时,若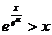 恒成立,求实数
恒成立,求实数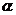 的取值范围.
的取值范围.
解:(Ⅰ)函数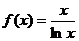 的定义域为
的定义域为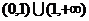 ,
2分
,
2分
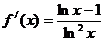 ,令
,令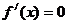 ,解得
,解得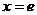 ,列表
,列表
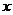 |
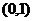 |
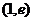 |
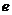 |
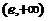 |
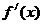 |
- |
- |
0 |
+ |
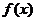 |
单调递减 |
单调递减 |
极小值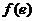 |
单调递增 |
由表得函数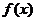 的单调减区间为
的单调减区间为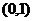 ,
,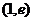 ;极小值为
;极小值为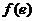 =
=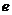 ,无极大值. 6分
,无极大值. 6分
(Ⅱ)因为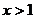 ,所以
,所以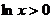
 在
在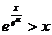 两边取自然对数,
两边取自然对数,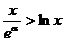 ,即
,即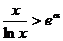 ,
12分
,
12分
由(1)知 的最小值为
的最小值为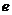 ,所以只需
,所以只需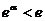 ,即
,即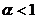 .
14分
.
14分
6.(山东省临沂高三数学(理工)教学质量监测) 已知函数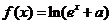 (
(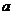 为常数)是R上的奇函数,函数g(x)=
为常数)是R上的奇函数,函数g(x)=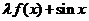 是区间
是区间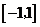 上的减函数.
上的减函数.
(Ⅰ)求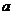 的值;
的值;
(Ⅱ)若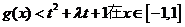 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程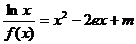 的根的个数.
的根的个数.
解:(Ⅰ) 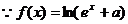 是奇函数,
是奇函数,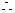
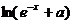 =
=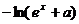 ……1分
……1分
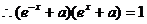 ,
,
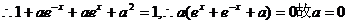 . ……………3分
. ……………3分
(Ⅱ)由(1)知: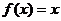 ,
,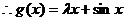 ,
,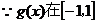 上单调递减,
上单调递减,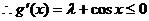
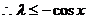
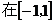 上恒成立,
上恒成立,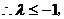 ……………5分
……………5分
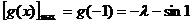 ,
,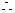 只需
只需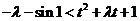 ,
,
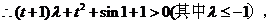 恒成立,
恒成立,
令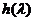 =
=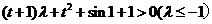 ,则
,则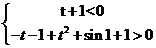 ,
,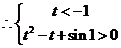 ,而
,而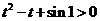 恒成立,
恒成立,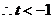 ……………8分
……………8分
(Ⅲ) 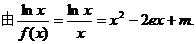 ,
…………………………9分
,
…………………………9分
令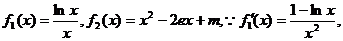
当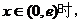
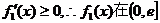 上为增函数;
上为增函数;
当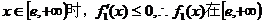 为减函数;
为减函数;
当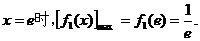 而
而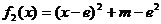 ,……………11分
,……………11分
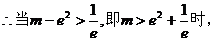 方程无解;
方程无解;
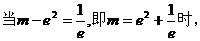 方程有一个根;
方程有一个根;
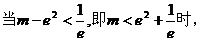 方程有两个根。 …………………………14分
方程有两个根。 …………………………14分
5.(山东省临朐一中2010届高三上学期) 设定义在R的函数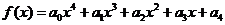 ,
,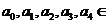 R. 当
R. 当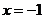 时,
时,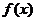 取得极大值
取得极大值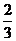 ,且函数
,且函数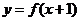 的图象关于点
的图象关于点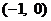 对称.
对称.
(I)求函数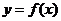 的表达式;
的表达式;
(II)判断函数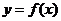 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间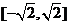 上,并说明理由;
上,并说明理由;
 (III)设
(III)设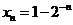 ,
,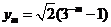 (
(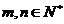 ),求证:
),求证: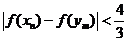 .
.
解:(I)将函数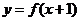 的图象向右平移一个单位得到函数
的图象向右平移一个单位得到函数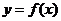 的图象,
的图象,
∴ 函数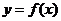 的图象关于点
的图象关于点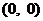 对称,即
对称,即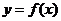 为奇函数.
为奇函数.
∴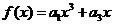 .
……………………………..2分
.
……………………………..2分
由题意可得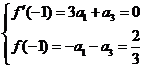 ,解得
,解得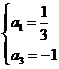 .
.
∴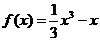 .
……………………………..4分
.
……………………………..4分
 (II)存在满足题意的两点.
……………………………..6分
(II)存在满足题意的两点.
……………………………..6分
由(I)得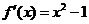 .
.
假设存在两切点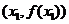 ,
,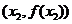 ,且
,且 .
.
则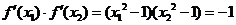 .
.
∵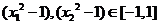 ,∴
,∴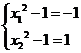 或
或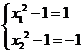 ,
,
即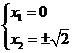 或
或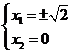 .
.
从而可求得两点的坐标分别为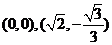 或
或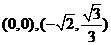 .
.
…………………………….9分
(III)∵当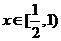 时,
时,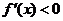 ,∴
,∴ 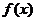 在
在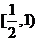 上递减.
上递减.
由已知得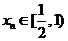 ,∴
,∴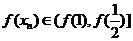 ,即
,即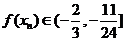 .
.
……………………………..11分
又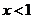 时,
时,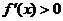 ;
;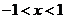 时,
时,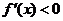 ,
,
∴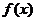 在
在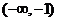 上递增,
上递增,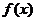 在
在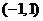 上递减.
上递减.
∵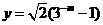 ,∴
,∴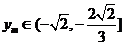 .
.
∵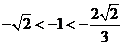 ,且
,且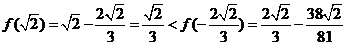 ,
,
∴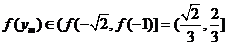 .
……………………………13分
.
……………………………13分
 ∴
∴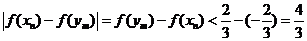 . ………………………..14分
. ………………………..14分
4.(2010届沈阳市四校协作体高三联考) 已知函数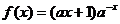 ,
,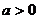 且
且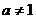 .
.
(I)讨论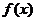 的单调性,并求出极值点
的单调性,并求出极值点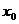 .
.
(II)若(I)中的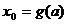 .求
.求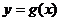 在
在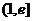 上的最小值.
上的最小值.
解:(I)当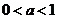 时,
时, 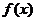 在
在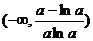 上单调递减,在
上单调递减,在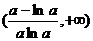 上单调递增, ――――――――――――――――――――――――――――――――(3分)
上单调递增, ――――――――――――――――――――――――――――――――(3分)
当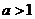 时,
时, 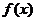 在上
在上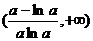 单调递减,在
单调递减,在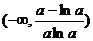 上单调递增. ――(5分)
上单调递增. ――(5分)
极值点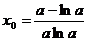 ―――――――――――――――――――――――――――(6分)
―――――――――――――――――――――――――――(6分)
(II)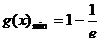 ――――――――――――――――――――――――――(12分)
――――――――――――――――――――――――――(12分)
3.(福建厦门外国语学校2009年11月高三月考试卷)
已知函数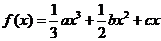 .
.
(Ⅰ)若函数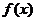 有三个零点
有三个零点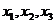 ,且
,且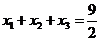 ,
,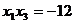 ,
,
求函数 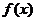 的单调区间;
的单调区间;
(Ⅱ)若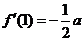 ,
,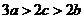 ,试问:导函数
,试问:导函数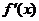 在区间(0,2)内是否有零点,
在区间(0,2)内是否有零点,
并说明理由.
(Ⅲ)在(Ⅱ)的条件下,若导函数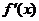 的两个零点之间的距离不小于
的两个零点之间的距离不小于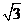 ,求
,求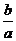 的取值范围.
的取值范围.
[解](I)因为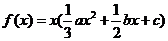 ,又
,又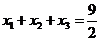 ,
,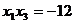 则
则
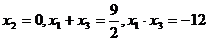 (1分)
(1分)
因为x1,x3是方程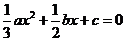 的两根,则
的两根,则
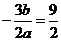 ,
,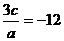 ,.即
,.即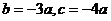 (3分)
(3分)
从而: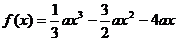 ,
,
所以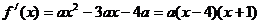 .
.
令 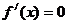 解得:
解得: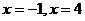 (4分)
(4分)
故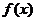 的单调递减区间是(1,4),单调递增区间是
的单调递减区间是(1,4),单调递增区间是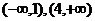 。 (6分)
。 (6分)
(Ⅱ)因为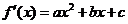 ,
,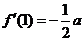 ,所以
,所以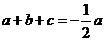 ,即
,即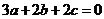 .
.
因为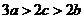 ,所以
,所以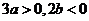 ,即
,即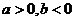 . (7分)
. (7分)
于是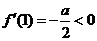 ,
,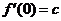 ,
,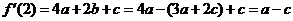 . (8分)
. (8分)
(1)当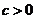 时,因为
时,因为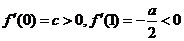 ,则
,则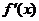 在区间
在区间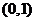 内至少有一个零点.
(9分)
内至少有一个零点.
(9分)
(2)当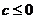 时,因为
时,因为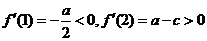 ,则
,则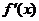 在区间(1,2)内至少有一零点.
在区间(1,2)内至少有一零点.
故导函数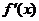 在区间(0,2)内至少有一个零点.
(10分)
在区间(0,2)内至少有一个零点.
(10分)
(Ⅲ)设m,n是导函数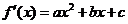 的两个零点,则
的两个零点,则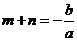 ,
,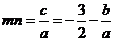 .
.
所以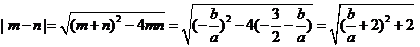 .
.
由已知,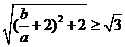 ,则
,则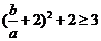 ,即
,即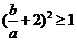 .
.
所以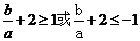 ,即
,即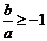 或
或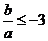 .
(12分)
.
(12分)
又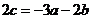 ,
,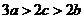 ,所以
,所以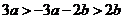 ,即
,即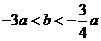 .
.
因为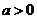 ,所以
,所以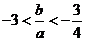 .
.
综上分析,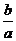 的取值范围是
的取值范围是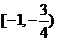 . (14分)
. (14分)
2.(绵阳中学2010届高三12月月考)已知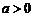 且
且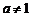 ,函数
,函数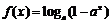 。
。
(1)求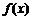 的定义域,并判断
的定义域,并判断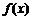 的单调性;(2)若
的单调性;(2)若 ,求
,求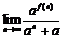
(3)当 (e为自然对数的底数),设
(e为自然对数的底数),设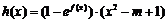 ,若
,若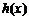 有极值。求m的取值范围及
有极值。求m的取值范围及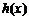 的极值
的极值

1.(北京市东城区示范校2009-2010学年度第一学期联考)设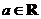 ,函数
,函数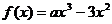 .
.
(Ⅰ)若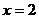 是函数
是函数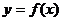 的极值点,求实数
的极值点,求实数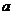 的值;
的值;
(Ⅱ)若函数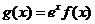 在
在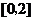 上是单调减函数,求实数
上是单调减函数,求实数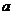 的取值范围.
的取值范围.
解:(Ⅰ)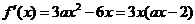 .
.
因为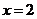 是函数
是函数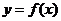 的极值点,所以
的极值点,所以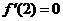 ,即
,即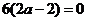 ,
,
所以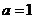 .经检验,当
.经检验,当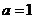 时,
时,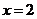 是函数
是函数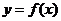 的极值点.
的极值点.
即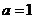 .
…………………6分
.
…………………6分
(Ⅱ)由题设,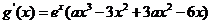 ,又
,又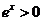 ,
,
所以,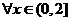 ,
,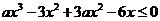 ,
,
这等价于,不等式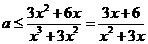 对
对 恒成立.
恒成立.
令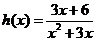 (
( ),
),
则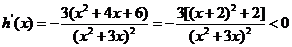 ,
,
所以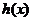 在区间
在区间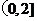 上是减函数,
上是减函数,
所以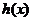 的最小值为
的最小值为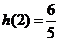 .
.
所以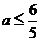 .即实数
.即实数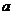 的取值范围为
的取值范围为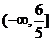 . …………………13分
. …………………13分
24.(1)染色体 DNA (2)蛋白质 DNA 细胞核 (3)双螺旋 基因 (4)染色体


24.(8分)右图是染色体和DNA的关系图,相信你一定会通过仔细的观察做出最准确的回答。
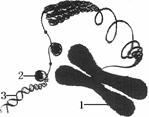 (1)图中[1]是 ;[2]是蛋白质;[3]是 。
(1)图中[1]是 ;[2]是蛋白质;[3]是 。
(2)[1]主要是由 和 组成,位于细胞中的 内。
(3)[3]具有规则的 结构,其上有与遗传相关的小“片断”,这就是 。
(4)在生物细胞分裂过程中,无论细胞分裂多少次, 的数目是保持不变的。这对于生物物种的稳定具有特别重要的意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com