
11.某研究性学习小组对春季昼夜温差大小与某花卉种子发芽多少之间的关系进行研究,他们分别记录了3月1日至3月5日的每天昼夜温差与实验室每天每100颗种子浸泡后的发芽数,得到如下资料:
|
日 期 |
3月1日 |
3月2日 |
3月3日 |
3月4日 |
3月5日 |
温差 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数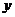 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
(1)从3月1日至3月5日中任选2天,记发芽的种子数分别为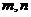 ,求事件“
,求事件“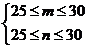 ”的概率.
”的概率.
(2)甲,乙两位同学都发现种子的发芽率与昼夜温差近似成线性关系,给出的拟合直线分别为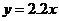 与
与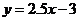 ,试利用“最小平方法(也称最小二乘法)的思想”,判断哪条直线拟合程度更好.
,试利用“最小平方法(也称最小二乘法)的思想”,判断哪条直线拟合程度更好.
10.将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为5的概率; (2)两数中至少有一个奇数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率.
9.元旦期间,某商场举行抽奖促销活动,现将装有编号为1,2,3,4四个小球的抽奖箱,从中抽出一个小球,记下号码后放回抽奖箱,搅匀后再抽出一个小球,两个小球号码之和不小于7中一等奖,等于6中二等奖,等于5中三等奖。
(1)求中二等奖的概率; (2)求中奖的概率。
8.潮州统计局就某地居民的月收入调查了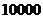 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在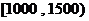 )。
)。

(1)求居民月收入在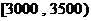 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这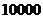 人中用
人中用
分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在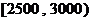 的这段应抽多少人?
的这段应抽多少人?
7.设AB=6,在线段AB上任取两点(端点A、B除外),将线段AB分成了三条线段,
(1)若分成的三条线段的长度均为正整数,求这三条线段可以构成三角形的概率;
(2)若分成的三条线段的长度均为正实数,求这三条线段可以构成三角形的概率.
6、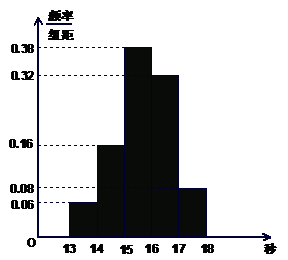 某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:每一组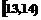 ;第二组
;第二组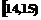 ……第五组
……第五组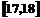 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒
认为良好,求该班在这次百米测试中
成绩良好的人数;
(II)设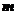 、
、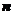 表示该班某两位同学的百米
表示该班某两位同学的百米
测试成绩,且已知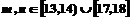 .
.
求事件“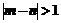 ”的概率.
”的概率.
5.甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船 不需要等等码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求它们中的任何一条船 不需要等待码头空出的概率.
4..(浙江省嘉兴市文)设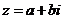 ,a,b∈R,将一个骰子连续抛掷两次,第一次得到的点数为a,第二次得到的点数为b,则使复数z2为纯虚数的概率为 ▲ .
,a,b∈R,将一个骰子连续抛掷两次,第一次得到的点数为a,第二次得到的点数为b,则使复数z2为纯虚数的概率为 ▲ .
3. (2009年浙江省杭州市数学试题(文))从1,2,3,4,5,6这6个数字中, 任取2个数字相加, 其和为偶数的概率是 ______ .
2.(台州市2008学年第一学期理文)用2、3、4组成无重复数字的三位数,这些数被4整除的概率是
A. B.
B.
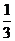 C.
C.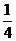 D.
D.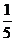
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com