
15. 解:(Ⅰ)基本事件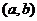 共有36个,方程有正根等价于
共有36个,方程有正根等价于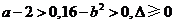 ,即
,即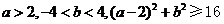 。设“方程有两个正根”为事件
。设“方程有两个正根”为事件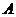 ,则事件
,则事件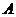 包含的基本事件为
包含的基本事件为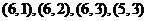 共4个,故所求的概率为
共4个,故所求的概率为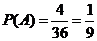 ;
;
(Ⅱ)试验的全部结果构成区域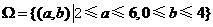 ,其面积为
,其面积为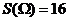
设“方程无实根”为事件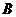 ,则构成事件
,则构成事件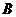 的区域为
的区域为
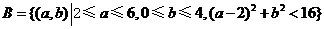 ,其面积为
,其面积为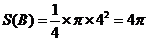
故所求的概率为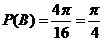
14. 解:(Ⅰ)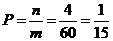
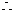 某同学被抽到的概率为
某同学被抽到的概率为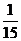 ………………2分
………………2分
设有 名男同学,则
名男同学,则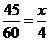 ,
,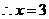
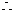 男、女同学的人数分别为
男、女同学的人数分别为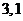 ………………4分
………………4分
(Ⅱ)把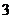 名男同学和
名男同学和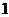 名女同学记为
名女同学记为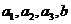 ,则选取两名同学的基本事件有
,则选取两名同学的基本事件有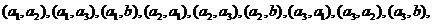
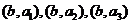 共
共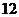 种,其中有一名女同学的有
种,其中有一名女同学的有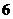 种
种
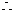 选出的两名同学中恰有一名女同学的概率为
选出的两名同学中恰有一名女同学的概率为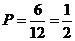 ……………………………8分
……………………………8分
(Ⅲ)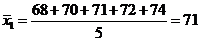 ,
,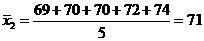
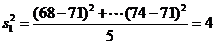 ,
,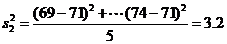
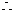 第二同学的实验更稳定………………………12分
第二同学的实验更稳定………………………12分
13. 解:(Ⅰ)依题意,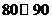 间的频率为:10×0.025=0.25 ……………2分
间的频率为:10×0.025=0.25 ……………2分
频数为: 40×0.25=10 …………………… ……………4分
(Ⅱ)这次环保知识竞赛成绩的平均数、众数、中位数分
别是:71、75、73.3 ……………………………… ……………8分
(Ⅲ)因为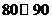 有10人,
有10人,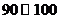 共有2人,从中任选2人,
共有2人,从中任选2人,
共有12×11÷2=66种,设分在同组记为事件A,分在同一组的有
10×9÷2+1=46种,
所以 P(A)=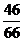 =
=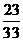 ……………………………… ……………12分
……………………………… ……………12分
12. 解:(1)点P所在的区域为圆x2+y2=8的内部(含边界)满足|x|≤2,|y|≤2的点的区域为正方形ABCD的内部(含边界)……………………………………2分
∴ 所求的概率P1=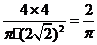 ……………………………………6分
……………………………………6分
(2)满足x,y∈z,且|x|<2,|y|<2的点有9个,满足x,y∈z且x2+y2≤8的点有25个。………………………………………………………………10分
∴ 所求的概率P2=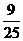 。……………………………………………12分
。……………………………………………12分
11. 解:(1)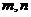 的取值情况有
的取值情况有
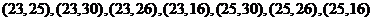 ,
,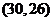 ,
,
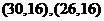 .基本事件总数为10. …3分
.基本事件总数为10. …3分
设“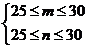 ”为事件
”为事件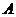 ,则事件
,则事件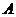 包含的基本事件为
包含的基本事件为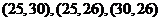
所以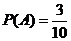 ,故事件“
,故事件“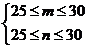 ”的概率为
”的概率为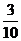 .
……7分
.
……7分
(2)将甲,乙所作拟合直线分别计算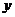 的值得到下表:
的值得到下表:
 |
10 |
11 |
13 |
12 |
8 |
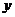 |
23 |
25 |
30 |
26 |
16 |
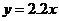 |
22 |
24.2 |
28.6 |
26.4 |
17.6 |
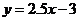 |
22 |
24.5 |
29.5 |
27 |
17 |
用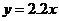 作为拟合直线时,所得到的
作为拟合直线时,所得到的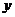 值与
值与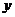 的实际值的差的平方和为
的实际值的差的平方和为
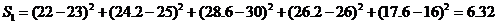 ………9分
………9分
用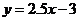 作为拟合直线时,所得到的
作为拟合直线时,所得到的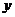 值与
值与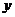 的实际值的差的平方和为
的实际值的差的平方和为
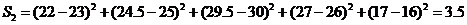 ………11分
………11分
由于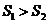 ,故用直线
,故用直线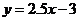 的拟合效果好.
………12分
的拟合效果好.
………12分
10. 解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件 1分
(1)记“两数之和为5”为事件A,则事件A中含有4个基本事件,
所以P(A)=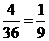 ;答:两数之和为5的概率为
;答:两数之和为5的概率为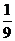 .
4分
.
4分
(2)记“两数中至少有一个奇数”为事件B,则事件B与“两数均为偶数”为对立事件,所以P(B)=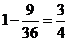 ;答:两数中至少有一个奇数的概率
;答:两数中至少有一个奇数的概率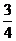 .
8分
.
8分
(3)基本事件总数为36,点(x,y)在圆x2+y2=15的内部记为事件C,则C包含8个事件,所以P(C)=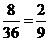 .答:点(x,y)在圆x2+y2=15的内部的概率
.答:点(x,y)在圆x2+y2=15的内部的概率 .
.
9. 解:抽出号码对为:(1,1),(1,2),(1,3),(1,4),(2,1) (2,2),(2,3),(2,4),(3,1),,(3,2),(3,3),(3,4) ,(4,1),(4,2),(4,3),(4,4) ,共16种,每个号码被抽到是等可能的。……… 3分
(1)
两个小球号码之和等于6共有(2,4),(3,3),(4,2)3种,故中二等奖的概率为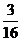 6分
6分
(2)
中一等奖的号码对为(3,4) ,(4,3),(4,4);中三等奖的号码对为(1,4),(2,3),(3,2),(4,1) … 10分
故中奖的概率为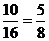 … 12分
… 12分
8. 解:(1)月收入在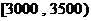 的频率为
的频率为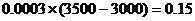 。
。 分
分
(2)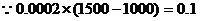 ,
,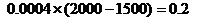 ,
,
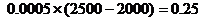 ,
,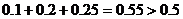 …… 6分
…… 6分
所以,样本数据的中位数为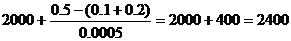 (元);… 8分
(元);… 8分
(3)居民月收入在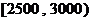 的频率为
的频率为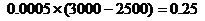 ,
,
所以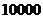 人中月收入在
人中月收入在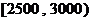 的人数为
的人数为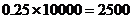 (人),
(人),
再从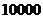 人用分层抽样方法抽出
人用分层抽样方法抽出 人,则月收入在
人,则月收入在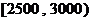 的应该抽取
的应该抽取
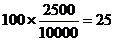 人。
………… 12分
人。
………… 12分
7.答案:解(1)若分成的三条线段的长度均为正整数,则三条线段的长度的所有可能为:

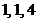 ;
;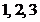 ,
,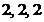 共3种情况,其中只有三条线段为
共3种情况,其中只有三条线段为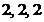 时能构成三角形,则构成三角形的概率
时能构成三角形,则构成三角形的概率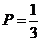 .………………4分
.………………4分
(2)设其中两条线段长度分别为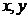 ,则第三条线段长
,则第三条线段长
度为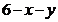 ,则全部结果所构成的区域为:
,则全部结果所构成的区域为:
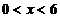 ,
,
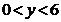 ,
,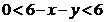 ,即为
,即为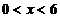 ,
,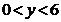 ,
,
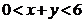 ,所表示的平面区域为三角形
,所表示的平面区域为三角形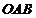 ;……6分
;……6分
若三条线段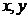 ,
,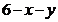 能构成三角形,则还要满足
能构成三角形,则还要满足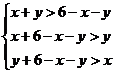 ,即为
,即为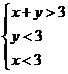 ,所表示的平面区域为三角形
,所表示的平面区域为三角形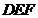 ,……………………………………9分
,……………………………………9分
由几何概型知,所求的概率为 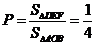 .……………………12分
.……………………12分
6、答案:解:(1)由直方图知,成绩在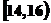 内的人数为:
内的人数为: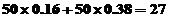 (人)
(人)
所以该班成绩良好的人数为27人.
(2)由直方图知,成绩在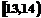 的人数为
的人数为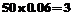 人,
人,
设为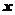 、
、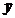 、
、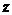 ;成绩在
;成绩在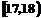 的人数为
的人数为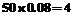 人,设为
人,设为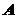 、
、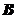 、
、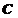 、
、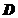 .
.
若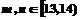 时,有
时,有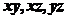 3种情况;
3种情况;
若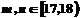 时,有
时,有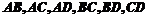 6种情况;
6种情况;
若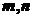 分别在
分别在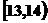 和
和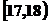 内时,
内时,
|
|
A |
B |
C |
D |
|
x |
xA |
xB |
xC |
xD |
|
y |
yA |
yB |
yC |
yD |
|
z |
zA |
zB |
zC |
zD |
共有12种情况.所以基本事件总数为21种,事件“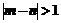 ”所包含的基本事件个数有12种.∴P(
”所包含的基本事件个数有12种.∴P(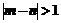 )=
)=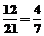
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com