
20.[解答](Ⅰ)分别以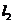 、
、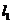 为
为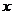 轴,
轴, 轴建立如图坐标系.据题意得
轴建立如图坐标系.据题意得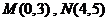 ,
,
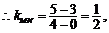
 线段
线段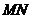 的垂直平分线方程为:
的垂直平分线方程为: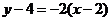 ),
),
故圆心A的坐标为(4,0),
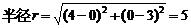 ,
,
∴弧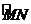 的方程:
的方程: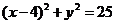 (0≤x≤4,y≥3)
(0≤x≤4,y≥3)
(Ⅱ)设校址选在B(a,0)(a>4),
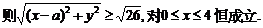
整理得: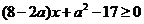 ,对0≤x≤4恒成立(﹡)
,对0≤x≤4恒成立(﹡)
令
∵a>4
∴ ∴
∴ 在[0,4]上为减函数
在[0,4]上为减函数
∴要使(﹡)恒成立,当且仅当
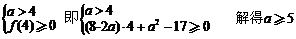 ,
,
即校址选在距 最近5km的地方.
最近5km的地方.
20.(本小题满分13分)
如图,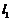 、
、 是通过某城市开发区中心
是通过某城市开发区中心 的两条南北和东西走向的街道,连接
的两条南北和东西走向的街道,连接 、
、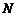 两地之间的铁路线是圆心在
两地之间的铁路线是圆心在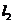 上的一段圆弧.若点
上的一段圆弧.若点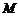 在点
在点 正北方向,且
正北方向,且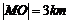 ,点
,点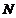 到
到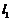 、
、 的距离分别为
的距离分别为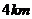 和
和 .
.
(Ⅰ)建立适当坐标系,求铁路线所在圆弧的方程;
(Ⅱ)若该城市的某中学拟在点 正东方向选址建分校,考虑环境问题,要求校址到点
正东方向选址建分校,考虑环境问题,要求校址到点 的距离大于
的距离大于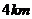 ,并且铁路线上任意一点到校址的距离不能少于
,并且铁路线上任意一点到校址的距离不能少于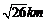 ,求该校址距点O的最近距离(注:校址视为一个点).
,求该校址距点O的最近距离(注:校址视为一个点).
19. [解答] (Ⅰ)设点 ,由
,由 得
得 ,
,
由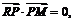 得
得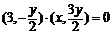 即
即 .
.
(Ⅱ)由题意可知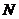 为抛物线
为抛物线 的焦点,且
的焦点,且 为过焦点
为过焦点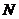 的直线与抛物线
的直线与抛物线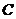 的两个交点.
的两个交点.
当直线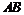 斜率不存在时,得A(1,2),B(1,-2),|AB|
斜率不存在时,得A(1,2),B(1,-2),|AB|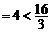 ,不合题意;
,不合题意;
当直线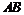 斜率存在且不为0时,设
斜率存在且不为0时,设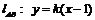 ,代入
,代入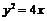 得
得
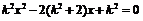
则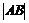
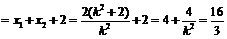 ,解得
,解得 ,
,
代入原方程得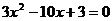 ,得
,得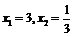 或
或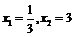 ,
,
由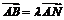 ,得
,得 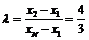 或4.
或4.
19.(本小题满分12分)
已知点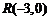 ,点
,点 在
在 轴上,点
轴上,点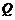 在
在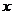 轴的正半轴上,点
轴的正半轴上,点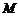 在直线
在直线 上 ,且满足
上 ,且满足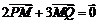 ,
, .
.
(Ⅰ)当点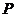 在
在 轴上移动时,求点
轴上移动时,求点 的轨迹
的轨迹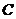 的方程;
的方程;
(Ⅱ)设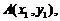
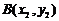 为轨迹
为轨迹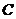 上两点,且
上两点,且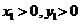 ,
, ,求实数
,求实数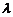 ,使
,使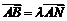 ,且
,且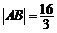 .
.
18.[解答]由题意知: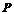 、
、 关于原点对称,设
关于原点对称,设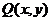 是函数
是函数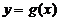 图像上任一点,则
图像上任一点,则 是
是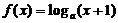 上的点,所以
上的点,所以 ,于是
,于是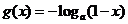 .
.
(Ⅰ)由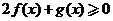 得
得 ,
,
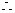
 时,不等式的解集为
时,不等式的解集为
(Ⅱ) ,
,
当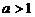 ,且
,且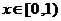 时,总有
时,总有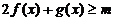 恒成立,
恒成立,
即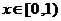 时,
时,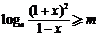 恒成立,
恒成立,
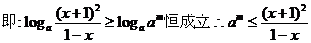 ,
,
设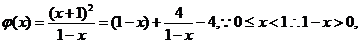
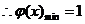 (此时
(此时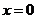 ),
),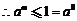 ,
, 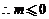 .
.
18.(本小题满分12分)
已知函数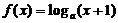 ,点
,点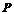 是函数
是函数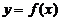 图像上任意一点,点
图像上任意一点,点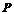 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数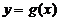 的图像.
的图像.
(Ⅰ)当 时,解关于
时,解关于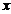 的不等式
的不等式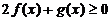 ;
;
(Ⅱ)当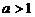 ,且
,且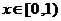 时,总有
时,总有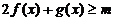 恒成立,求
恒成立,求 的取值范围.
的取值范围.
17.[解答](Ⅰ)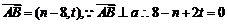
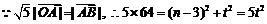 , 得
, 得 ,
,
 或
或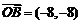 .
.
(Ⅱ)
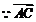 与
与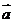 共线,
共线, 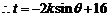
 ,
,
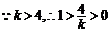 ,
,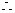 当
当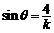 时,
时,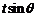 取最大值为
取最大值为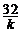 ,
,
由 ,得
,得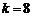 ,此时
,此时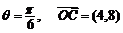 ,
,
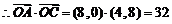 .
.
17.(本小题满分12分)
在平面直角坐标系中, 为坐标原点,已知
为坐标原点,已知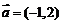 ,点
,点

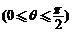 .
.
(Ⅰ)若 且
且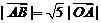 ,求向量
,求向量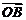 ;
;
(Ⅱ)若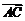 与
与 共线,当
共线,当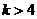 时,且
时,且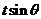 取最大值为4时,求
取最大值为4时,求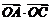 .
.
16.[解答] (Ⅰ)
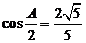 ,
, ,
,
由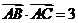 得
得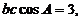
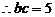 ,
,
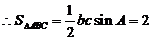
(Ⅱ)对于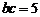 ,又
,又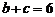 ,
,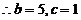 或
或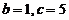 ,
,
由余弦定理得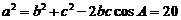 ,
,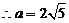 .
.
16.(本小题满分12分)
在 中,角
中,角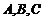 所对的边分别为
所对的边分别为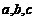 ,且满足
,且满足 ,
,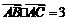 .
.
(Ⅰ)求 的面积; (Ⅱ)若
的面积; (Ⅱ)若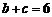 ,求
,求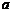 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com