
8.已知命题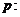 方程
方程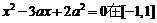 上有解;命题
上有解;命题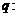 只有一个实数
只有一个实数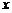 满足不等式
满足不等式
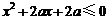 ,若命题“
,若命题“ 或
或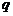 ”是假命题,则
”是假命题,则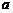 的取值范围是( )
的取值范围是( )
A.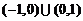 B.
B.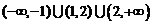
C.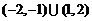 D.
D.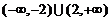
7.已知函数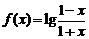 ,若
,若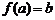 ,则
,则 等于( )
等于( )
A.b B.-b C. D.
D.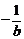
6.已知函数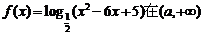 上是减函数,则a的取值范围是( )
上是减函数,则a的取值范围是( )
A.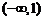 B.
B.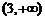 C.
C.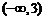 D.
D.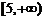
5. 已知命题p: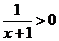 ;命题q:
;命题q: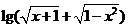 有意义.则
有意义.则 是
是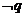 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.函数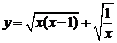 的定义域为( )
的定义域为( )
A.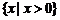 B.
B.
C.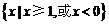 D.
D.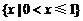
3.集合 ,从A到B的映射f满足
,从A到B的映射f满足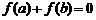 ,那么这样的映射f的个数有( )
,那么这样的映射f的个数有( )
A.2个 B.3个 C.5个 D.8个
2.满足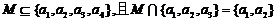 的集合M的个数是( )
的集合M的个数是( )
A.1个 B.2个 C.3个 D.4个
填入答题卡相应的格子中.
1.设集合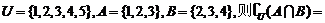 ( )
( )
A.{2,3} B.{1,4,5} C.{4,5} D.{1,5}
21.[解答](Ⅰ)令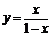 ,解得
,解得 ,由
,由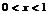 ,解得
,解得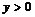 ,
,
∴函数 的反函数
的反函数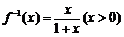 ,则
,则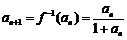 ,得
,得 .
.
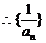 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故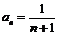 .
.
(Ⅱ)∵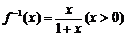 ,∴
,∴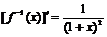 ,
,
∴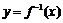 在点
在点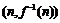 处的切线方程为
处的切线方程为 ,
,
令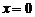 , 得
, 得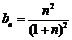 ,∴
,∴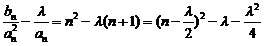 ,
,
∵仅当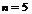 时取得最小值,∴
时取得最小值,∴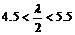 ,解之
,解之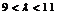 ,
,
∴ 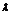 的取值范围为
的取值范围为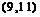 .
.
(Ⅲ)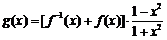
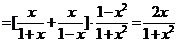 ,
,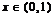 .
.
则 ,
,
因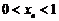 ,则
,则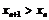 ,显然
,显然 .
.
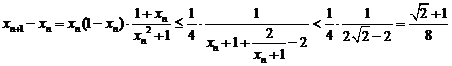
∴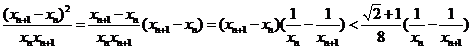
∴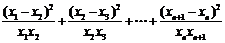
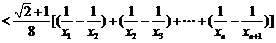
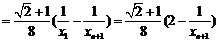
∵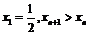 ,∴
,∴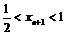 ,
,
∴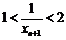 ,∴
,∴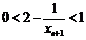
∴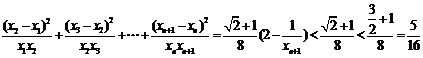 .
.
21.(本小题满分14分)
已知函数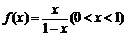 的反函数为
的反函数为 ,数列
,数列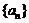 和
和 满足:
满足: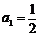 ,
,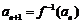 ,函数
,函数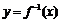 的图象在点
的图象在点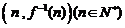 处的切线在
处的切线在 轴上的截距为
轴上的截距为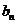 .
.
(Ⅰ)求数列{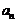 }的通项公式;
}的通项公式;
(Ⅱ)若数列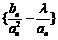 的项仅
的项仅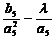 最小,求
最小,求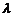 的取值范围;
的取值范围;
(Ⅲ)令函数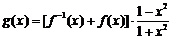 ,
,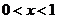 ,数列
,数列 满足:
满足: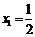 ,
,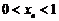 ,且
,且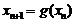 ,其中
,其中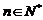 .证明:
.证明: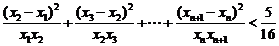 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com