
1.求曲线的轨迹方程常采用的方法有直接法、定义法、代入法、参数法
(1)直接法 直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程
(2)定义法 若动点轨迹的条件符合某一基本轨迹的定义(如椭圆、双曲线、抛物线、圆等),可用定义直接探求
(3)相关点法 根据相关点所满足的方程,通过转换而求动点的轨迹方程
(4)参数法 若动点的坐标(x,y)中的x,y分别随另一变量的变化而变化,我们可以以这个变量为参数,建立轨迹的参数方程
求轨迹方程,一定要注意轨迹的纯粹性和完备性 要注意区别“轨迹”与“轨迹方程”是两个不同的概念
要注意区别“轨迹”与“轨迹方程”是两个不同的概念
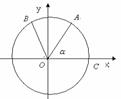
12. 如图, 为坐标原点,A、B是单位圆O上的动点,C是圆
为坐标原点,A、B是单位圆O上的动点,C是圆 与x轴正半轴的交点,设
与x轴正半轴的交点,设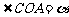 .
.
 (Ⅰ)当点A的坐标为
(Ⅰ)当点A的坐标为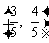 时,求
时,求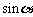 的值;(Ⅱ)若
的值;(Ⅱ)若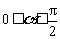 ,且当点A、B在圆
,且当点A、B在圆 上沿逆时针方向移动时,总有
上沿逆时针方向移动时,总有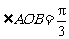 ,试求BC的取值范围.
,试求BC的取值范围.
考点突破专题十七 常见的数学思想方法(2)
039轨迹方程
[自我提醒]
11. 双曲线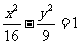 的右焦点为F,点A(5,4),点P在双曲线的右支上,则4PF-5PA的最大值为
.
的右焦点为F,点A(5,4),点P在双曲线的右支上,则4PF-5PA的最大值为
.
9.已知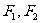 分别为椭圆
分别为椭圆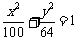 的左右焦点,椭圆内的一点M的坐标为(2,-6),P为椭圆上的一个动点,求
的左右焦点,椭圆内的一点M的坐标为(2,-6),P为椭圆上的一个动点,求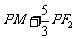 的最小值
.
的最小值
.
10在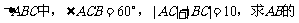 中点M的轨迹方程
.
中点M的轨迹方程
.
7. 若点A的坐标为(3,2),F为抛物线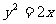 的焦点,点P是抛物线上的一动点,则求
的焦点,点P是抛物线上的一动点,则求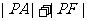 取得最小值时点P的坐标
.
取得最小值时点P的坐标
.
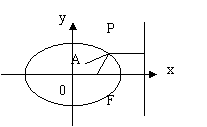 8.已知点A(1,2)在椭圆
8.已知点A(1,2)在椭圆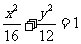 内,F的坐标为(2,0),在椭圆上求一点P 使
内,F的坐标为(2,0),在椭圆上求一点P 使 最小,P( , )
最小,P( , )
6.(08海南宁夏理11)已知点P在抛物线 上,那么点P到点
上,那么点P到点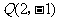 的距离与点P到抛物线焦点距离之和取得最小值时,点P .
的距离与点P到抛物线焦点距离之和取得最小值时,点P .
5.(08北京理4)若点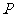 到直线
到直线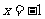 的距离比它到点
的距离比它到点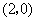 的距离小1,则点
的距离小1,则点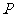 的轨迹为
.
的轨迹为
.
4.(浙江理12文13))已知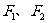 为椭圆
为椭圆 的两个焦点,过
的两个焦点,过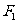 的直线交椭圆于A、B两点 若
的直线交椭圆于A、B两点 若 ,则
,则 =
.
=
.
3. 、
、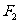 是双曲线
是双曲线 的焦点,点
的焦点,点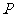 在双曲线上.若
在双曲线上.若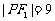 则
则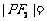 .
.
2.平面内有一长度为4的线段 ,动点
,动点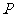 满足
满足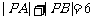 ,则
,则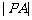 的取值范围是
.
的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com