22．(本小题满分12分)

已知：如图，一个等腰直角三角形的硬纸片ABC中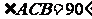，，AC=4cm，CD是斜边上的高，沿CD把△ABC折成直二面角.

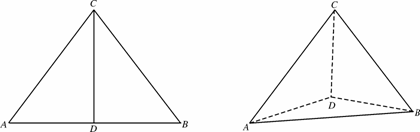
(1)如果你手中只有一把能度量长度的直尺，应该如何确定A，B的位置，使二面角A-CD-B是直二面角？证明你的结论；

(2)试在三棱锥的面ABC上确定一点P，使DP与平面ABC内任意一条直线都垂直，试证明你的结论.

(3)如果在折成的三棱锥内有一个小球，求出小球半径的最大值.

21．(本小题满分12分)

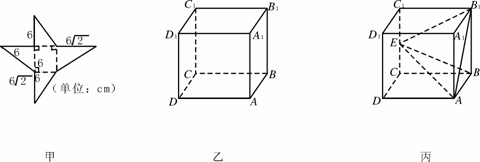
如图(甲)所示为一几何体的展开图.

(1)沿图中虚线将它们折叠起来，是哪一种几何体？试用文字描述并画图；

(2)需要多少个这样的几何体才能拼成一个棱长为6cm的正方体？请你在图(乙)中棱长为6cm的正方体ABCD-A₁B₁C₁D₁中指出这几个几何体的名称.

(3)如图(丙)所示，设棱长为6cm的正方体ABCD-A₁B₁C₁D₁的棱CC₁的中点为E，试求：

①(文)异面直线EB与AB₁所成角的大小；

②(理)平面AB₁E与平面ABC所成二面角(锐角)的大小.

20．(本小题满分12分)

如图，已知直三棱柱ABC-A₁B₁C₁的侧棱长为2，底面△ABC是等腰直角三角形，且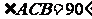，AC=2，D是AA₁的中点.

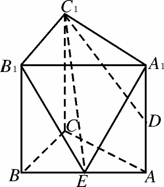(1)求异面直线AB和C₁D所成的角；

(2)设E是AB上一点，试确定E的位置，

使得A₁E⊥C₁D.

(3)(只理科做)在(2)的条件下，求点D

到平面B₁C₁E₁的距离.

19．(本小题满分12分)

如图，在四棱锥P-ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB，PB的中点.

(1)求证：EF⊥CD；

(2)在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论.

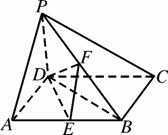(3)(只理科做)求DB与平面DEF所成角的大小.

18．(本小题满分12分)

已知直四棱柱ABCD-A′B′C′D′的底面是菱形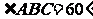，，E、F

分别是棱CC′与BB′上的点，且EC=BC=2FB=2.

(1)求证：平面AEF⊥平面AA′C′C；

(2)求截面AEF与底面ABCD所成二面角的大小.

17．(本小题满分10分)

如图，已知四棱锥P-ABCD的底面是直角梯形. ，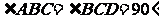

AB=BC=PB=PC=2CD，侧面PBC⊥底面ABCD.

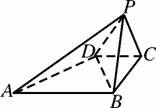(1)PA与BD是否相互垂直，请证明你的结论.

(2)求二面角P-BD-C的大小.

(3)求证：平面PAD⊥平面PAB.

16．(理)设有四个条件：

①平面γ与平面α、β所成的锐二面角相等；

②直线a∥b，a⊥平面α、b⊥平面β；

③a，b是异面直线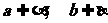，，且∥，∥；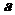

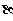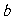④平面内距离为d的两条平行直线在平面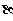内的射影仍为两条距离为d的平行直线；

其中能推出∥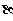的条件有　　　　　　　　　　　　 .

(文)有如下四个命题：

①平面和平面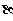垂直的充要条件是平面内至少有一条直线与平面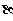垂直；

②平面和平面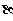平行的一个必要不充分条件是内有无数条直线与平面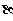平行；

③直线a与平面平行的一个充分不必要条件是平面内有一条直线与直线a平行；

④两条直线平行是这两条直线在一个平面内的射影互相平行的既不充分也不必要条件.

其中正确的序号是　　　　　　　　　　 .

15．在平行四边形ABCD中，AB=AC=1，∠ACD=90°，将它沿对角线AC折起，使AB与CD成60°角，则B、D间的距离为　　　　　　　　　　　 .

14．三棱锥中，已知两相对棱长分别为16和18，其余四条棱长都是17，则此三棱锥的体积是　　　　　　　　　　　　 .

13．已知空间三点A(1，1，1)、B(-1，0，4)、C(2，-2，3)，则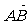与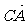的夹角θ的大小是　　　　　　　　　　 .