
9.已知椭圆 为圆心,以
为圆心,以 为半径作圆
为半径作圆 ,过点
,过点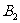
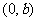 作圆
作圆 的两条切线,设切点分别为
的两条切线,设切点分别为 两点。
两点。
(1) 若过两个切点 的直线恰好经过点
的直线恰好经过点 时,求此椭圆的离心率;
时,求此椭圆的离心率;
(2) 若直线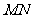 的斜率为-1,且原点到直线
的斜率为-1,且原点到直线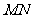 的距离为
的距离为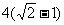 ,求此时的椭圆方程
,求此时的椭圆方程
(3) 是否存在椭圆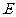 ,使得直线
,使得直线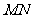 的斜率
的斜率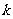 在区间
在区间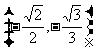 内取值?若存在,求出椭圆的离心率
内取值?若存在,求出椭圆的离心率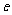 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
第17讲 圆锥曲线的方程和性质
[课前热身]
8.已知抛物线C: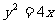 的顶点为O,过点(
的顶点为O,过点(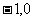 )且平行于向量
)且平行于向量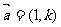 的直线与抛物线C交于A、B两点,当实数
的直线与抛物线C交于A、B两点,当实数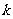 变化时:
变化时:
(1) 求证: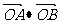 是一个与
是一个与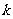 无关的常数;
无关的常数;
(2) 若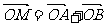 ,求
,求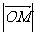 的最小值。
的最小值。
7.抛物线的顶点在原点,焦点在x轴上,它的准线过双曲线的一个焦点,且与双曲线实轴垂直,已知抛物线与双曲线的交点为(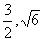 ),求抛物线与双曲线的方程。
),求抛物线与双曲线的方程。
6.P在椭圆 上运动,
上运动, 分别在两圆
分别在两圆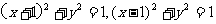
运动,则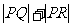 的最大值为
,最小值为
的最大值为
,最小值为
5.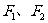 是双曲线
是双曲线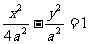 (
( )的两个焦点,P为双曲线上一点,
)的两个焦点,P为双曲线上一点,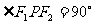 且
且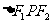 的面积为1,则
的面积为1,则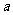 的值是
的值是
4.焦点在 轴上,以
轴上,以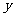 轴为准线,且到点
轴为准线,且到点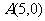 最近距离为
最近距离为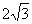 的一个抛物线的方程是( )
的一个抛物线的方程是( )
A. B.
B.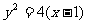 C.
C.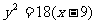 D.
D.
3. 椭圆的一个焦点是(2,1),相应准线方程是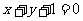 ,椭圆的短轴长为
,椭圆的短轴长为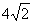 ,则椭圆的另一个焦点为( )
,则椭圆的另一个焦点为( )
A.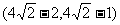 B.(
B.(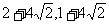 )C.
)C.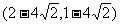 D.(6,5)
D.(6,5)
2. 椭圆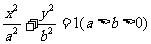 的两焦点为
的两焦点为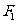 、
、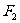 ,以
,以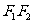 为边作正三角形,若椭圆恰好平分正三角形的另两边,则椭圆的离心率为( )
为边作正三角形,若椭圆恰好平分正三角形的另两边,则椭圆的离心率为( )
A.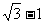 B.
B.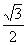 C.
C.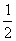 D.
D.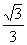
1.方程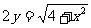 所表示的曲线是( )
所表示的曲线是( )
A.圆 B.椭圆上半部分 C.双曲线的一支 D.抛物线
3.
例3设PQ是过抛物线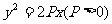 焦点F的一条弦,若P(
焦点F的一条弦,若P(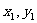 ),Q(
),Q( )且PQ的倾斜角为
)且PQ的倾斜角为
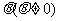 则有以下结论:①
则有以下结论:① ,
,
 ②
② ③
③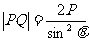 ④
④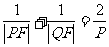
冲刺强化训练(17)
班级 姓名 学号 日期 月 日
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com