
16. 已知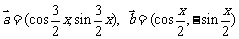 ,且
,且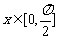 .
.
(1)求 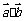 及
及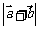 ; (2)求函数
; (2)求函数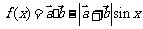 的最小值.
的最小值.
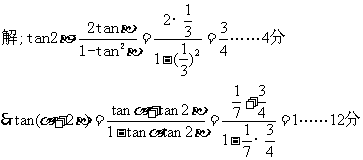
解:(1)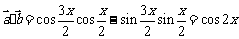 , 。。。。2分
, 。。。。2分
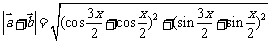
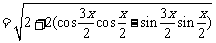
 .。。。。。4分
.。。。。。4分
∵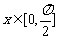 ,
∴
,
∴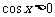 .
∴
.
∴ . 。。。。6分
. 。。。。6分
(2)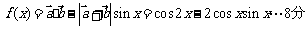
 .
.
答案整理:饶胜文
欢迎将错误反馈到zssxzb@
15.(2009年广东卷.理16)已知向量 与
与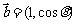 互相垂直,其中
互相垂直,其中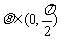 .
.
(1)求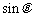 和
和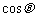 的值;
的值;
(2)若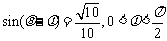 ,求
,求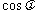 的值.
的值.
解:(1)∵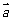 与
与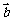 互相垂直,则
互相垂直,则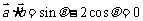 ,。。。2分
,。。。2分
即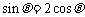 ,代入
,代入 ,解得
,解得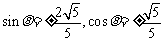 .。。。。6分
.。。。。6分
又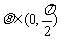 ,∴
,∴ .。。。8分
.。。。8分
(2)∵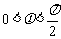 ,
,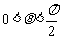 ,∴
,∴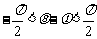 ,
,
则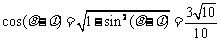 .。。。。。。10分
.。。。。。。10分
∴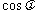
 .。。。。。12分
.。。。。。12分
14. 已知函数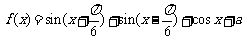 的最大值为1. (◎P147 12)
的最大值为1. (◎P147 12)
(1)求常数a的值; (2)求使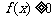 成立的x的取值集合.
成立的x的取值集合.

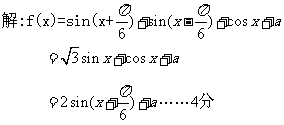

13. 已知函数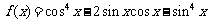 . (◎P147 10)
. (◎P147 10)
(1)求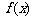 的最小正周期; (2)当
的最小正周期; (2)当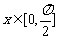 时,求
时,求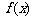 的最小值以及取得最小值时x的集合.
的最小值以及取得最小值时x的集合.


12. 已知函数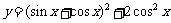 . (◎P147 9)
. (◎P147 9)
(1)求它的递减区间; (2)求它的最大值和最小值.

11. (1)(07年江苏卷.11)已知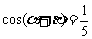 ,
,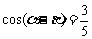 ,求
,求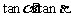 的值; (◎P146 7)
的值; (◎P146 7)
(2)已知 ,
, ,求
,求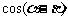 的值. (◎P147 B2)
的值. (◎P147 B2)
解:(1)∵ cos (α+β)=cosα
cosβ-sinα sinβ=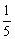 ①;
①;
cos (α-β)=
cosα cosβ+sinα sinβ= ②.。。。。。。。2分
②.。。。。。。。2分
①+②得cosα cosβ= , ②-①得 sinα sinβ=
, ②-①得 sinα sinβ=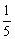 , 。。。。。14分
, 。。。。。14分
∴
tanα·tanβ=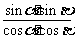 =
=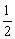 .。。。。。。。6分
.。。。。。。。6分

10. 已知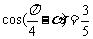 ,
,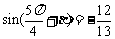 ,
,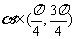 ,
,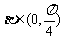 ,求
,求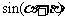 的值. (◎P146 2)
的值. (◎P146 2)
已知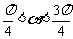 , 0<β<
, 0<β<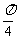 , cos(
, cos(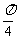 -α)=
-α)=  , sin(
, sin(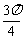 +β)=
+β)= 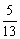 , 求sin(α+β)的值.
, 求sin(α+β)的值.
解:∵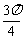 +β-(
+β-(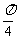 -α)=
-α)=  +(α+β),。。。。。。。2分
+(α+β),。。。。。。。2分
∴ sin(α+β)=-cos[ +(α+β)]=-cos[(
+(α+β)]=-cos[(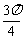 +β)-(
+β)-(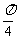 -α)]=-[cos(
-α)]=-[cos(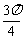 +β)cos(
+β)cos(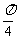 -α)+sin(
-α)+sin(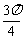 +β)sin(
+β)sin(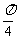 -α)] 。。。。。4分
-α)] 。。。。。4分
∵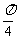 <α<
<α<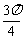

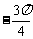 <-α<
<-α<

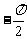 <
<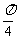 -α<0,
-α<0,
0<β<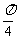

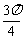 <
<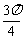 +β<π.。。。。。。6分
+β<π.。。。。。。6分
∴ sin(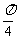 -α)=
-α)= =
=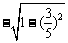 =
=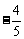 ,。。。。8分
,。。。。8分
cos(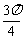 +β)=
+β)=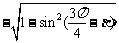 =
=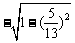 =
=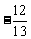 .。。。。。10分
.。。。。。10分
由(1)得:
sin(α+β)=-[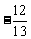 ×
× +
+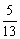 ×(
×(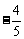 )]=
)]=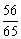 .。。。。。12分
.。。。。。12分
9. 已知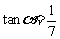 ,
,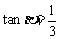 ,求
,求 的值. (◎P138 17)
的值. (◎P138 17)
8. 已知 ,
, ,
,
(1)求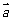 与
与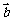 的夹角
的夹角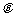 ;
;
(2)若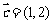 ,且
,且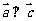 ,试求
,试求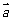 .
.
解:(1)∵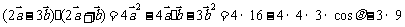 =61,
=61,
∴ 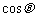 =
=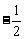 ,。。。。。。4分
,。。。。。。4分
∴ 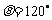 .。。。。。。。。。。6分
.。。。。。。。。。。6分
(2)设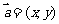 ,则
,则
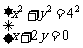 ,解得
,解得 或
或 .。。。。。10分
.。。。。。10分
所以,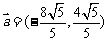 或
或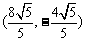 .。。。。。。。12分
.。。。。。。。12分
7. 平面上三个力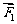 、
、 、
、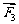 作用于一点且处于平衡状态,
作用于一点且处于平衡状态,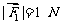 ,
,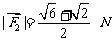 ,
,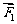 与
与 的夹角为
的夹角为 ,求:(1)
,求:(1)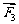 的大小; (2)
的大小; (2)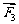 与
与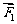 夹角的大小. (◎P113 4)
夹角的大小. (◎P113 4)
解:∵三个力平衡,∴F1+F2+F3=0,。。。。。。2分
∴|F3|=|F1+F2|=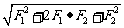 =
=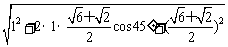 =
=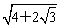 =
=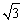 +1,。。。。。。。。。。。。。。6分
+1,。。。。。。。。。。。。。。6分
而-F3与F1的夹角可由余弦定理求得,
cos<-F3,F1>=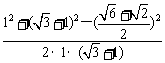 =
=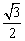 ,∴-F3与F1的夹角为30°. 。。10分
,∴-F3与F1的夹角为30°. 。。10分
则F3与F1的夹角为180°-30°=150°. 。。。。。。12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com