
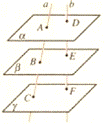
5. 如图,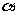 ∥
∥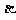 ∥
∥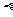 ,直线
,直线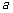 与
与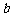 分别交
分别交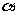 ,
,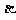 ,
,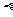 于点
于点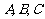 和点
和点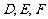 ,求证:
,求证: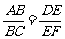 . (◎P63
B3)
. (◎P63
B3)
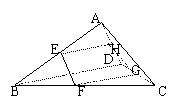
4. 已知空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且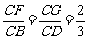 .
.
求证:(1)E、F、G、H四点共面;(2)三条直线EF、GH、AC交于一点. (☆P21 例3)
3. 直角三角形三边长分别是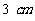 、
、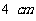 、
、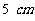 ,绕三边旋转一周分别形成三个几何体. 想象并说出三个几何体的结构,画出它们的三视图,求出它们的表面积和体积. (◎P36 10)
,绕三边旋转一周分别形成三个几何体. 想象并说出三个几何体的结构,画出它们的三视图,求出它们的表面积和体积. (◎P36 10)
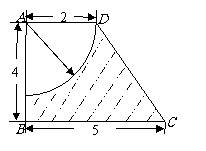
2. 如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积. (☆P15 例2)
1. 在圆锥底面半径为1 cm,高为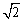 cm,其中有一个内接正方体,求这个内接正方体的棱长.(☆P3 例3)
cm,其中有一个内接正方体,求这个内接正方体的棱长.(☆P3 例3)
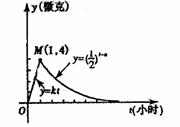
16. 某医药研究所开发一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线.
(1)写出服药后y与t之间的函数关系式y=f(t); (2)据进一步测定:每毫升血液中含药量不少于0.25微克时,治疗疾病有效.求服药一次治疗疾病有效的时间?(☆P45 例3)
15. 如图,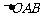 是边长为2的正三角形,记
是边长为2的正三角形,记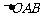 位于直线
位于直线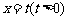 左侧的图形的面积为
左侧的图形的面积为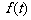 . 试求函数
. 试求函数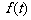 的解析式,并画出函数
的解析式,并画出函数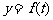 的图象. (◎P126
B2)
的图象. (◎P126
B2)

14. 某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3万件,为了以后估计每个月的产量,以这三个月的产品数据为依据. 用一个函数模拟产品的月产量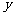 与月份数
与月份数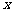 的关系,模拟函数可选用二次函数
的关系,模拟函数可选用二次函数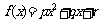 (其中
(其中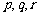 为常数,且
为常数,且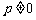 )或指数型函数
)或指数型函数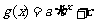 (其中
(其中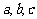 为常数),已知4月份该产品产量为1.37万件,请问用上述哪个函数模拟较好?说明理由.(☆P51 例2)
为常数),已知4月份该产品产量为1.37万件,请问用上述哪个函数模拟较好?说明理由.(☆P51 例2)
13. 家用冰箱使用的氟化物的释放破坏了大气上层臭氧层. 臭氧含量Q呈指数函数型变化,满足关系式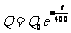 ,其中
,其中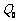 是臭氧的初始量. (1)随时间的增加,臭氧的含量是增加还是减少?
(2)多少年以后将会有一半的臭氧消失?
(参考数据:
是臭氧的初始量. (1)随时间的增加,臭氧的含量是增加还是减少?
(2)多少年以后将会有一半的臭氧消失?
(参考数据: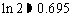 ) (☆P44 9)
) (☆P44 9)
12. 某商场经销一批进货单价为40元的商品,销售单价与日均销售量的关系如下表:
|
销售单价/元 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
|
日均销售量/个 |
48 |
46 |
44 |
42 |
40 |
38 |
36 |
为了获取最大利润,售价定为多少时较为合理? (☆P49 例1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com