
10. 三角形的三个顶点是A(4,0)、B(6,7)、C(0,3). (◎P101 B1)
(1)求BC边上的高所在直线的方程; (2)求BC边上的中线所在直线的方程;
(3)求BC边的垂直平分线的方程.
解:(1)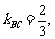 所以BC边上的高所在直线
所以BC边上的高所在直线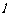 的斜率为
的斜率为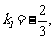 又
又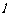 过点
过点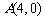 ,所以直线
,所以直线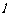 的方程为
的方程为
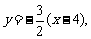 即
即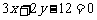 ;……………………………..4分
;……………………………..4分
(2)BC中点坐标为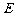
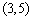 ,所以
,所以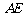 所在直线的方程为
所在直线的方程为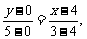 即
即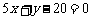 。..8分
。..8分
(3)易知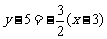 即
即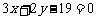 为所求。…………………………………….12分
为所求。…………………………………….12分
9. 求过点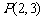 ,并且在两轴上的截距相等的直线方程. (◎P100 9)
,并且在两轴上的截距相等的直线方程. (◎P100 9)
解:因为直线l经过点P(2,3),且在x轴,y轴上的截距相等,所以
(1)当直线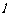 过原点时,它的方程为
过原点时,它的方程为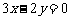 ;……………………………5分
;……………………………5分
(2)当直线不过原点时,设它的方程为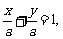 由已知得
由已知得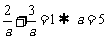 ,
,
所以,直线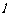 的方程为
的方程为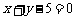 。……………………………………….11分
。……………………………………….11分
综上,直线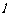 的方程为
的方程为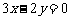 ,或者
,或者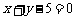 。……………..12分
。……………..12分
8. 已知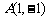 ,
,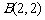 ,
,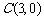 ,求点D的坐标,使直线CD⊥AB,且CB∥AD.(◎P90 8)
,求点D的坐标,使直线CD⊥AB,且CB∥AD.(◎P90 8)
解:设点D的坐标为(x,y),由已知得,直线AB的斜率KAB=3,……………2分.
直线CD的斜率KCD=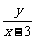 , 直线CB的斜率KCB=-2, 直线AD的斜率KAD=
, 直线CB的斜率KCB=-2, 直线AD的斜率KAD=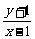 。
。
……………………………………………………………………………8分
由CD⊥AB,且CB∥AD,得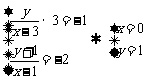 ,………11分
,………11分
所以点D的坐标是(0,1)……………………………………..12分
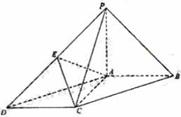
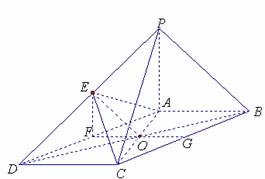
7.(06年北京卷)如图,在底面为平行四边形的四棱锥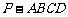 中,
中,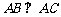 ,
,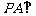 平面
平面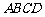 ,且
,且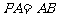 ,点
,点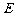 是
是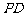 的中点.
的中点.
(1)求证: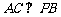 ; (2)求证:
; (2)求证: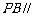 平面
平面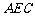 ;(3)求二面角
;(3)求二面角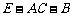 的大小. (☆P38 9)
的大小. (☆P38 9)
 解:(1)∵ PA⊥平面 ABCD,
解:(1)∵ PA⊥平面 ABCD,
∴AB 是 PB 在平面 ABCD 上的射影.
又∵AB⊥AC,AC 平面ABCD, ∴AC⊥PB. ……4分
平面ABCD, ∴AC⊥PB. ……4分
(2)连接BD,与 AC 相交于 O,连接 EO.
∵ABCD 是平行四边形, ∴O 是 BD 的中点
又 E 是 PD 的中点,∴EO∥PB.
又 PB 平面 AEC,EO
平面 AEC,EO 平面 AEC,
平面 AEC,
∴PB∥平面 AEC……………………………..8分
(3)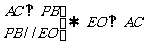
取AD的中点F,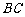 的中点
的中点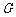 ,连
,连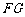 ,则
,则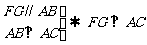
所以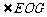 是所求二面角的平面角,且
是所求二面角的平面角,且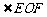 与
与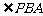 对应相等。
对应相等。
易知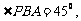 由图可知,
由图可知,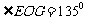 为所求。……………12分
为所求。……………12分
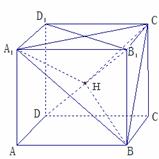
6. 如图,在正方体ABCD-A1B1C1D1中. (◎P79 B2)
求证:(1)B1D⊥平面A1C1B; (2)B1D与平面A1C1B的交点设为H,则点H是△A1C1B的垂心.
 证明:(1)连
证明:(1)连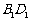 ,
,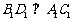 ,又
,又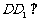 面
面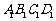 ,
,
所以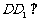
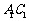 ,
,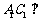 面
面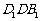 ,因此
,因此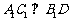 。
。
同理可证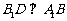 ,所以B1D⊥平面A1C1B。……6分
,所以B1D⊥平面A1C1B。……6分
(2)连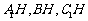 ,由
,由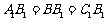 ,得
,得
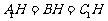 ,因此点
,因此点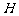 为
为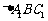 的外心。
的外心。
又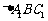 为正三角形,所以
为正三角形,所以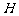 是
是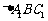 的中心,
的中心,
也是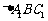 的重心。………….…………………. 12分
的重心。………….…………………. 12分
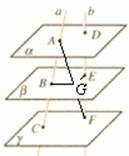
5. 如图,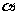 ∥
∥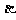 ∥
∥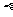 ,直线
,直线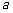 与
与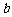 分别交
分别交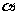 ,
,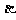 ,
,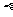 于点
于点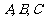 和点
和点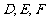 ,求证:
,求证: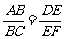 . (◎P63 B3)
. (◎P63 B3)
证明:连结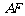 ,交
,交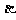 于
于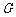 ,连
,连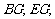 …………3分
…………3分
则由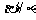 得
得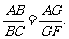 ……………………7分
……………………7分
由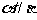 得
得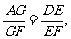 ………………..10分
………………..10分
所以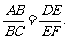 ………………………..12分
………………………..12分
4.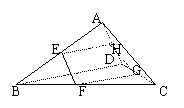 已知空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且
已知空间四边形ABCD中,E、H分别是AB、AD的中点,F、G分别是BC、CD上的点,且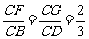 .
.
求证:(1)E、F、G、H四点共面;(2)三条直线EF、GH、AC交于一点. (☆P21 例3)
证明:(1) 在△ABD和△CBD中,
∵ E、H分别是AB和CD的中点, ∴ EH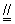
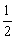 BD…………….3分
BD…………….3分
又 ∵ 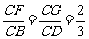 , ∴ FG
, ∴ FG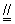
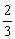 BD.
BD.
∴ EH∥FG. 分
所以,E、F、G、H四点共面.--------------------------------------------7分
(2)由(1)可知,EH∥FG ,且EH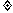 FG,即直线EF,GH是梯形的两腰,
FG,即直线EF,GH是梯形的两腰,
所以它们的延长线必相交于一点P. ……………………………9分
∵ AC是EF和GH分别所在平面ABC和平面ADC的交线,而点P是上述两平面的公共点,
∴ 由公理3知P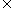 AC. ………………………11分
AC. ………………………11分
 所以,三条直线EF、GH、AC交于一点……..12分
所以,三条直线EF、GH、AC交于一点……..12分
3. 直角三角形三边长分别是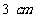 、
、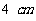 、
、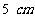 ,绕三边旋转一周分别形成三个几何体. 想象并说出三个几何体的结构,画出它们的三视图,求出它们的表面积和体积. (◎P36 10)
,绕三边旋转一周分别形成三个几何体. 想象并说出三个几何体的结构,画出它们的三视图,求出它们的表面积和体积. (◎P36 10)
解:以绕5cm边旋转为例,其直观图、正视图与侧视图、俯视图依次分别为:
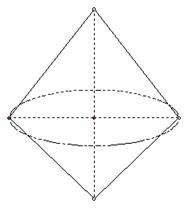
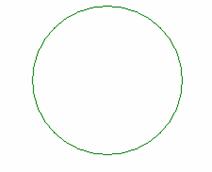
…………………………………………………………………………………………………………..2分
其表面是两个扇形的表面,所以其表面积为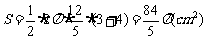 ;-----------------3分
;-----------------3分
体积为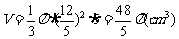 。………………………………………………….4分
。………………………………………………….4分
同理可求得当绕3cm边旋转时,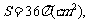
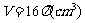 。…………………….8分
。…………………….8分
得当绕4cm边旋转时,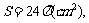
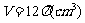 。……………………………….12分
。……………………………….12分
(图形略)
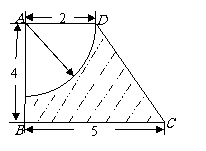
2. 如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积. (☆P15 例2)
解:由题意知, 所求旋转体的表面积由三部分组成:
圆台下底面、侧面和一半球面. ……………………………………….3分
S半球=8π , S圆台侧=35π ,S圆台底=25π.
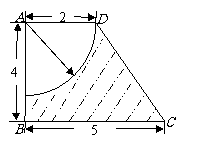 故所求几何体的表面积为68π ………………………………………..7分
故所求几何体的表面积为68π ………………………………………..7分
由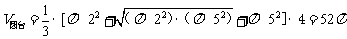 ,………9分
,………9分
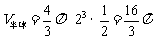 …………………………………………….11分
…………………………………………….11分
所以,旋转体的体积为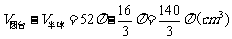 ……12分
……12分
1. 圆锥底面半径为1 cm,高为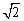 cm,其中有一个内接正方体,求这个内接正方体的棱长. (☆P3 例3)
cm,其中有一个内接正方体,求这个内接正方体的棱长. (☆P3 例3)
 解:过圆锥的顶点S和正方体底面的一条对角线CD作圆锥的截面,得圆锥的轴截面SEF,正方体对角面CDD1C1,如图所示. …………………2分
解:过圆锥的顶点S和正方体底面的一条对角线CD作圆锥的截面,得圆锥的轴截面SEF,正方体对角面CDD1C1,如图所示. …………………2分
设正方体棱长为x,则CC1=x,C1D1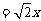 。
。
作SO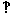 EF于O,则SO
EF于O,则SO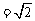 ,OE=1,……………………………….5分
,OE=1,……………………………….5分

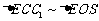 , ∴
, ∴ 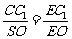 ,即
,即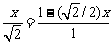 ………..10分
………..10分
 ∴
∴ 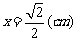 , 即内接正方体棱长为
, 即内接正方体棱长为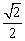 cm……………………….12分
cm……………………….12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com