
∴()2+4a= 4.
∴b2= (4-4a)a2...................................5分
(Ⅱ)由(1)知b2= (4-4a)a2≥0,且0<a≤1
令函数g(a)= (4-4a)a2= -4a3+4a2(0<a≤1)
g′(a)= -12a2+8a= 8a(1-a)
令g'(a)= 0 ∴a1= 0,a2= .
函数g(a)在(0,)上为增函数,(,1)上为减函数.
∴g(a)max= g()= .
∴b2≤.
∴|b|≤..........................................................12分
.
∴(|x1|+|x2|)2= (x2+x1)2-4x1x2= 4.
 ∴x1、x2 两根异号
∴x1、x2 两根异号
∴|x1|+|x2|=| x2-x1|
20、解:(Ⅰ)由题意知f′(x)= ax2+bx-a2,且f′(x)= 0的两根为x1、x2.
∴x1+x2= - x1x2= -a
所以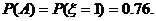
当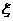 =3时,函数
=3时,函数 上不单调递增,
上不单调递增,
当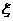 =1时,函数
=1时,函数 上单调递增,
上单调递增,
解法二: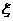 的可能取值为1,3.
的可能取值为1,3.
从而 ............................12
............................12
要使 上单调递增,当且仅当
上单调递增,当且仅当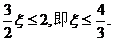
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com