
2.下列有关物质性质的比较顺序中,不正确的是 
A.热稳定性:HF<HCl<HBr<HI 
B.微粒半径:K+>Na+>Mg2+>Al3+
C.酸性:HClO4>H2SO4>H3PO4>H2SiO3
D.熔点:Li<Na<K<Rb
1.迄今为止,生成化合物的种类最多的元素位于
A.ⅡA族 B.IA族 C.ⅣA族 D.ⅤA族
27.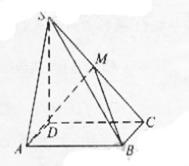 (2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)
(2009全国卷Ⅰ理)(本小题满分12分)(注意:在试题卷上作答无效)
如图,四棱锥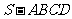 中,底面
中,底面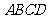 为矩形,
为矩形,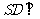 底面
底面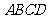 ,
, 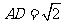
 ,点M在侧棱
,点M在侧棱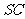 上,
上, =60°
=60°
(I)证明:M在侧棱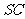 的中点
的中点
(II)求二面角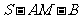 的大小。
的大小。
(I)解法一:作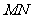 ∥
∥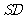 交
交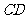 于N,作
于N,作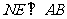 交
交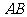 于E,
于E,
连ME、NB,则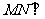 面
面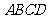 ,
,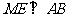 ,
,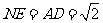
 设
设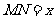 ,则
,则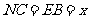 ,
,
在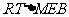 中,
中,

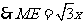 。
。
在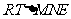 中由
中由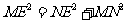
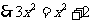
解得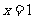 ,从而
,从而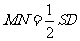
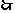 M为侧棱
M为侧棱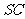 的中点M.
的中点M.
解法二:过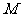 作
作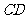 的平行线.
的平行线.
26.(2009江苏卷)(本小题满分14分)
如图,在直三棱柱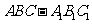 中,
中,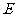 、
、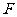 分别是
分别是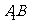 、
、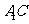 的中点,点
的中点,点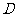 在
在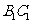 上,
上,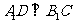 。
。
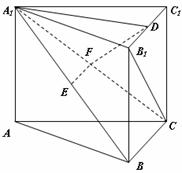 求证:(1)EF∥平面ABC;
求证:(1)EF∥平面ABC; 
(2)平面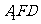
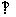 平面
平面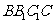 .
.
[解析] 本小题主要考查直线与平面、平面与平面得位置关系,考查空间想象能力、推理论证能力。满分14分。

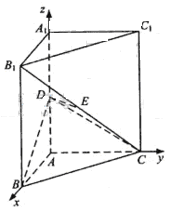
25.(2009全国卷Ⅱ文)(本小题满分12分). 

如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC 

(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
解析:本题考查线面垂直证明线面夹角的求法,第一问可取BC中点F,通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线,第二问先作出线面夹角,即证四边形AFED是正方形可证平面DEF⊥平面BDC,从而找到线面夹角求解。此题两问也可建立空间直角坐标系利用向量法求解。
解法一:(Ⅰ)取BC中点F,连接EF,则EF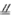
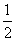
 ,从而EF
,从而EF DA。
DA。
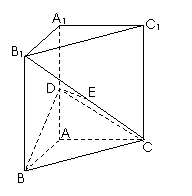

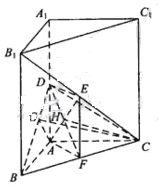
连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面 ,故AF⊥平面
,故AF⊥平面 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
(Ⅱ)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG=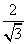 。又AB=2,BC=
。又AB=2,BC=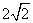 ,故AF=
,故AF=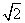 。
。
由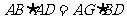 得2AD=
得2AD=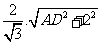 ,解得AD=
,解得AD=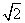 。
。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为 与平面BCD所成的角。.
与平面BCD所成的角。.


 因ADEF为正方形,AD=
因ADEF为正方形,AD=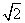 ,故EH=1,又EC=
,故EH=1,又EC= =2,
=2,
所以∠ECH=300,即 与平面BCD所成的角为300.
与平面BCD所成的角为300.
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A-xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则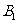 (1,0,2c),E(
(1,0,2c),E(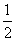 ,
,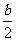 ,c).
,c).
于是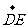 =(
=(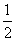 ,
,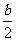 ,0),
,0), =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面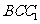 知DE⊥BC,
知DE⊥BC, 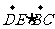 =0,求得b=1,所以 AB=AC。
=0,求得b=1,所以 AB=AC。
(Ⅱ)设平面BCD的法向量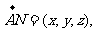 则
则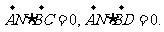
又 =(-1,1, 0),
=(-1,1, 0),
 =(-1,0,c),故
=(-1,0,c),故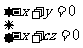


令x=1, 则y=1, z=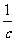 ,
,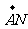 =(1,1,
=(1,1,
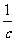 ).
).
又平面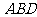 的法向量
的法向量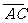 =(0,1,0)
=(0,1,0)
由二面角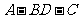 为60°知,
为60°知,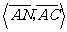 =60°,
=60°,
故 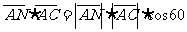 °,求得
°,求得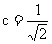


于是 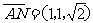 ,
, 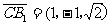
 ,
,
 °
°
所以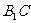 与平面
与平面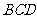 所成的角为30°
所成的角为30°
24.(2009年上海卷理)已知三个球的半径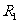 ,
,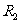 ,
,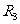 满足
满足 ,则它们的表面积
,则它们的表面积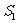 ,
,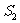 ,
,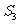 ,满足的等量关系是___________.
,满足的等量关系是___________. 



[答案]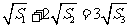
[解析]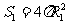 ,
,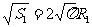 ,同理:
,同理: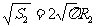
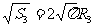 ,即R1=
,即R1=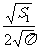 ,R2=
,R2=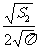 ,R3=
,R3=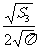 ,由
,由 得
得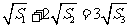
23.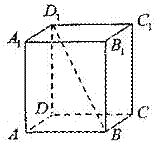 (2009年上海卷理)如图,若正四棱柱
(2009年上海卷理)如图,若正四棱柱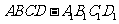 的底面连长为2,高 为4,则异面直线
的底面连长为2,高 为4,则异面直线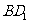 与AD所成角的大小是______________(结果用反三角函数表示).
与AD所成角的大小是______________(结果用反三角函数表示).
[答案]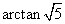
[解析]因为AD∥A1D1,异面直线BD1与AD所成角就是BD1与A1D1所在角,即∠A1D1B,
由勾股定理,得A1B=2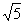 ,tan∠A1D1B=
,tan∠A1D1B=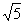 ,所以,∠A1D1B=
,所以,∠A1D1B=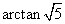 。
。
22.(2009福建卷文)如右图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为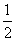 。则该集合体的俯视图可以是
。则该集合体的俯视图可以是
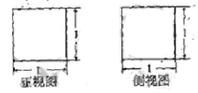
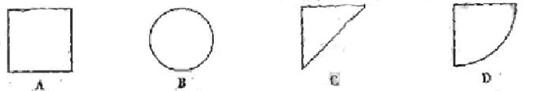
解析 解法1 由题意可知当俯视图是A时,即每个视图是变边长为1的正方形,那么此几何体是立方体,显然体积是1,注意到题目体积是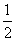 ,知其是立方体的一半,可知选C.
,知其是立方体的一半,可知选C.
解法2 当俯视图是A时,正方体的体积是1;当俯视图是B时,该几何体是圆柱,底面积是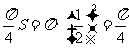 ,高为1,则体积是
,高为1,则体积是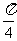 ;当俯视是C时,该几何是直三棱柱,故体积是
;当俯视是C时,该几何是直三棱柱,故体积是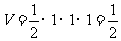 ,当俯视图是D时,该几何是圆柱切割而成,其体积是
,当俯视图是D时,该几何是圆柱切割而成,其体积是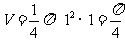 .故选C.
.故选C.
21. (2009四川卷理)如图,已知正三棱柱
(2009四川卷理)如图,已知正三棱柱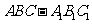 的各条棱长都相等,
的各条棱长都相等,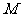 是侧 棱
是侧 棱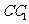 的中点,则异面直线
的中点,则异面直线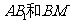 所成的角的大小是
。
所成的角的大小是
。
[考点定位]本小题考查异面直线的夹角,基础题。
解析:不妨设棱长为2,选择基向量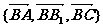 ,则
,则
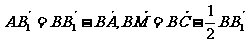
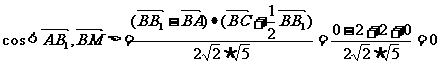 ,故填写
,故填写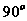 。
。
法2:取BC中点N,连结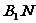 ,则
,则 面
面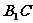 ,∴
,∴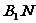 是
是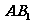 在面
在面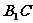 上的射影,由几何知识知
上的射影,由几何知识知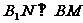 ,由三垂线定理得
,由三垂线定理得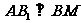 ,故填写
,故填写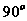 。
。
20.(2009陕西卷文)如图球O的半径为2,圆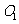 是一小圆,
是一小圆, ,A、B是圆
,A、B是圆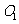 上两点,若
上两点,若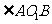 =
=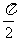 ,则A,B两点间的球面距离为
.
,则A,B两点间的球面距离为
.
答案: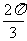
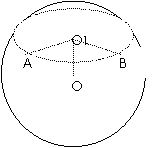
解析:由 ,
,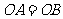 =2由勾股定理在
=2由勾股定理在 中
中
则有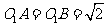 , 又
, 又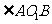 =
=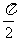 则
则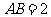 所以在
所以在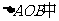 ,
,
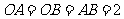 ,则
,则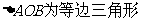 ,那么
,那么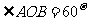 .
. 

由弧长公式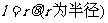 得
得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com