
1.(12分)
将质量均为xg的苹果果肉分别放在O2浓度不同的密闭容器中,一小时后测定O2的吸收量和CO2的释放量(如下表)。请回答:
|
O2相对浓度 变化量 |
0 |
1% |
2% |
3% |
5% |
7% |
10% |
15% |
20% |
25% |
|
O2吸收量(mol) |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
1 |
|
O2释放量(mol) |
1 |
0.8 |
0.6 |
0.5 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
1 |
(1)在O2相对浓度为3%时,苹果果肉细胞的呼吸方式为
;xg苹果果肉每小时分解葡萄糖 mol。
(2)贮藏苹果的环境中,适宜的O2相对浓度为 ,原因是
。
23. (本小题满分10分)
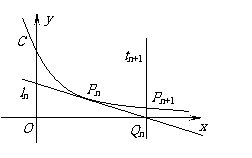 点
点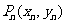 在曲线
在曲线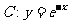 上,曲线C在点
上,曲线C在点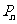 处的切线
处的切线 与
与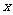 轴相交于点
轴相交于点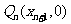 ,直线
,直线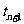 :
: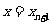 与曲线C相交于点
与曲线C相交于点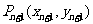 ,(
,(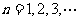 ).由曲线
).由曲线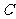 和直线
和直线 ,
,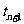 围成的图形面积记为
围成的图形面积记为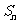 ,已知
,已知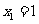 .
.
(Ⅰ)证明: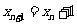 ;
;
(Ⅱ)求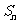 关于
关于 的表达式;
的表达式;
(Ⅲ)记数列 的前
的前 项之和为
项之和为 ,
,
求证: (
( ).
).
盐城市2009/2010学年度高三年级第一次调研
22.(本小题满分10分)
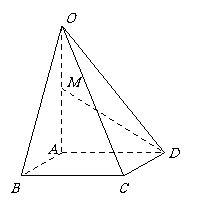 如图,在四棱锥
如图,在四棱锥 中,底面
中,底面 是边长为1的菱形,
是边长为1的菱形,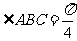 ,
,  底面
底面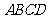 ,
, 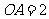 ,
,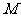 为
为 的中点.
的中点.
(Ⅰ)求异面直线AB与MD所成角的大小;
(Ⅱ)求平面 与平面
与平面 所成的二面角的余弦值.
所成的二面角的余弦值.
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4-1:几何证明选讲)
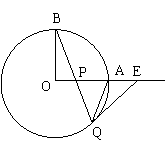 如图,已知
如图,已知 是
是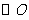 的半径,且
的半径,且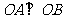 ,
,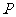 是线段
是线段 上一点,直线
上一点,直线 交
交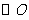 于点
于点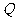 ,过
,过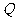 作
作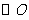 的切线交直线
的切线交直线 于点
于点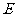 ,
,
求证: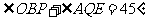 .
.
B.(选修4-2:矩阵与变换)
求矩阵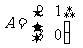 的特征值及对应的特征向量.
的特征值及对应的特征向量.
C.(选修4-4:坐标系与参数方程)
已知直线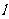 的参数方程:
的参数方程: (
(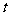 为参数)和圆
为参数)和圆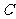 的极坐标方程:
的极坐标方程: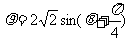 .
.
(Ⅰ)将直线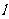 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆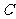 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)判断直线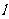 和圆
和圆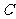 的位置关系.
的位置关系.
D.(选修4-5:不等式选讲)
已知函数 . 若不等式
. 若不等式
 恒成立,求实数
恒成立,求实数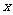 的范围.
的范围.
[必做题] 第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
20.(本小题满分16分)
已知函数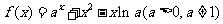 .
.
(Ⅰ)当 时,求证:函数
时,求证:函数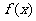 在
在 上单调递增;
上单调递增;
(Ⅱ)若函数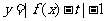 有三个零点,求
有三个零点,求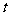 的值;
的值;
(Ⅲ)若存在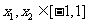 ,使得
,使得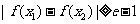 ,试求
,试求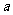 的取值范围.
的取值范围.
盐城市2009/2010学年度高三年级第一次调研考试
数学附加题部分
(本部分满分40分,考试时间30分钟)
19.(本小题满分16分)
已知数列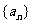 是以
是以 为公差的等差数列,数列
为公差的等差数列,数列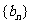 是以
是以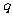 为公比的等比数列.
为公比的等比数列.
(Ⅰ)若数列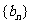 的前
的前 项和为
项和为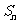 ,且
,且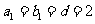 ,
, ,求整数
,求整数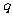 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问数列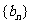 中是否存在一项
中是否存在一项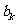 ,使得
,使得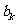 恰好可以表示为该数列中连续
恰好可以表示为该数列中连续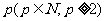 项的和?请说明理由;
项的和?请说明理由;
(Ⅲ)若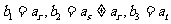 (其中
(其中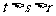 ,且(
,且( )是(
)是( )的约数),
)的约数),
求证:数列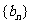 中每一项都是数列
中每一项都是数列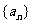 中的项.
中的项.
18.(本小题满分16分)
 已知⊙
已知⊙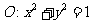 和点
和点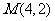 .
.
(Ⅰ)过点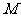 向⊙
向⊙ 引切线
引切线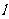 ,求直线
,求直线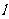 的方程;
的方程;
(Ⅱ)求以点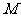 为圆心,且被直线
为圆心,且被直线 截得的弦长为
4的⊙
截得的弦长为
4的⊙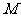 的方程;
的方程;
(Ⅲ)设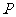 为(Ⅱ)中⊙
为(Ⅱ)中⊙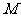 上任一点,过点
上任一点,过点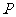 向⊙
向⊙ 引切线,切点为Q. 试探究:平面内是否存在一定点
引切线,切点为Q. 试探究:平面内是否存在一定点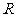 ,使得
,使得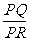 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
17.(本小题满分14分)
经市场调查,某旅游城市在过去的一个月内(以30天计),日旅游人数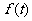 (万人)与时间
(万人)与时间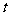 (天)的函数关系近似满足
(天)的函数关系近似满足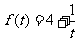 ,人均消费
,人均消费 (元)与时间
(元)与时间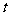 (天)的函数关系近似满足
(天)的函数关系近似满足 .
.
(Ⅰ)求该城市的旅游日收益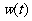 (万元)与时间
(万元)与时间 的函数关系式;
的函数关系式;
(Ⅱ)求该城市旅游日收益的最小值(万元).
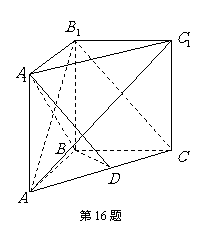
16.(本小题满分14分)
如图,在直三棱柱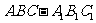 中,
中,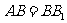 ,
,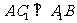 ,
,
 为
为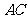 的中点.
的中点.
(Ⅰ)求证: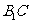 ∥平面
∥平面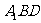 ;
;
(Ⅱ)求证:平面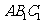 ⊥平面
⊥平面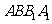 .
.
15.(本小题满分14分)
. 已知角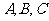 是
是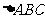 的内角,向量
的内角,向量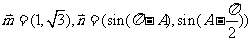 ,
, ⊥
⊥ .
.
(Ⅰ)求角A的大小;
(Ⅱ)求函数 的值域.
的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com