
19.(1)由条件: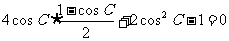
 ………………(3分)
………………(3分)
故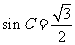 ,则
,则 ,
,
由 ,得
,得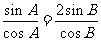 , 所以
, 所以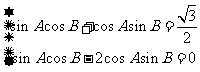 ,
,
得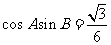 ,
, ,
,
所以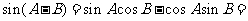
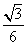 (7分)
(7分)
(2)由余弦定理:

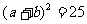
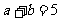
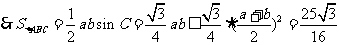
当且仅当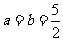 取得最大值.
(14分)
取得最大值.
(14分)
18.解:(1) ;…………………………………………4分
;…………………………………………4分
(2)提示: ,
, 的分布列为:
的分布列为:
 |
1 |
2 |
3 |
4 |
|
P |
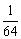 |
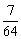 |
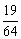 |
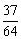 |
………………………………(建议对1个给2分)…………………………………………12分
故 .………………………………………………14分
.………………………………………………14分
16.2016 17.②③
11.90 12.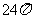 13.
13.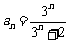 14.
14.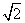 15.
15.
1.D 2.B 3.A 4.D 5.C 6.A 7.D 8.C 9.A 10.D
22.(本小题满分15分)
设函数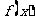 的导函数为
的导函数为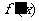 ,若
,若 ,则称点
,则称点 是函数
是函数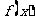 的一个驻点。已知函数
的一个驻点。已知函数
(1)若函数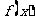 总存在有两个驻点
总存在有两个驻点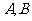 ,求
,求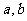 所满足的关系;
所满足的关系;
(2)若函数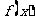 有两个驻点
有两个驻点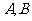 ,且存在
,且存在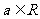 ,求
,求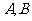 两个驻点在不等式
两个驻点在不等式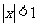 表示的区域内时实数
表示的区域内时实数 的范围;
的范围;
(3)若函数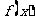 恰有一个驻点
恰有一个驻点 ,且存在
,且存在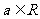 ,使驻点
,使驻点 在不等式
在不等式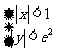 表示的区域内,证明:
表示的区域内,证明: .
.
浙江省杭州高级中学高三理科数学月考试卷(2010.3)
21. (本小题满分15分)
(本小题满分15分)
过点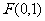 作直线
作直线 与抛物线
与抛物线 相交于两点
相交于两点  ,圆
,圆
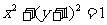
(1)若抛物线在点 处的切线恰好与圆
处的切线恰好与圆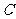 相切,求直线
相切,求直线 的方程;
的方程;
(2)过点 分别作圆
分别作圆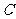 的切线
的切线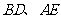 ,试求
,试求 的取值范围。
的取值范围。
20.(本小题满分14分)
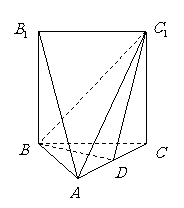
如图,五面体 中,
中, .底面
.底面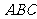 是正三角形,
是正三角形,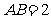 .四边形
.四边形 是矩形,二面角
是矩形,二面角  为直二面角.
为直二面角.
(1)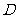 在
在 上运动,当
上运动,当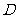 在何处时,有
在何处时,有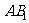 ∥平面
∥平面 ,并且说明理由;
,并且说明理由;
 (2)当
(2)当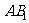 ∥平面
∥平面 时,求二面角
时,求二面角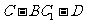 的余弦值.
的余弦值.
19.(本小题满分14分)
在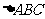 中,
中,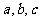 分别是角
分别是角 ,
, ,
,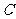 的对边,且
的对边,且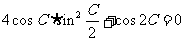 .
.
(1)若 ,求
,求 的值;
的值;
(2)若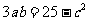 ,求
,求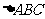 面积的最大值.
面积的最大值.
18.(本大题共14分)
一袋中装有分别标记着1,2,3,4数字的4只小球,每次从袋中取出一只球,设每只小球被取到的可能性相同.
(1)若每次取出的球不放回袋中,求恰好第三次取到标号为3的球的概率;
(2)若每次取出的球放回袋中,然后再取出一只球,现连续取三次球,若三次取出的球中标号最大的数字为 ,求
,求 的概率分布列与期望.
的概率分布列与期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com