人民币被誉为中国的名片。目前人民币一共发行了五套，一些风景被印在它们背面。读图4完成7-8题。　

7．图中四种地貌景观与其成因对应正确的是

　 　 A．甲--内外力共同作用　　 　　　　 B．乙--断层下陷　

C．丙--背斜顶部侵蚀　　 　　　　　 D．丁--冰川侵蚀

8．丁地所受侵蚀作用最强的季节是

　 　 A．春季　　 B．夏季　　 C．秋季　　 D．冬季　　

7.黑盒问题。

如果黑盒内只有电阻，分析时，从阻值最小的两点间开始。

例题分析

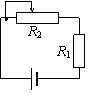例1：已知如图，E =6V，r =4Ω，R₁=2Ω，R₂的变化范围是0~10Ω。求：①电源的最大输出功率；②R₁上消耗的最大功率；③R₂上消耗的最大功率。

解：①R₂=2Ω时，外电阻等于内电阻，电源输出功率最大为2.25W；

②R₁是定植电阻，电流越大功率越大，所以R₂=0时R₁上消耗的功率最大为2W；

③把R₁也看成电源的一部分，等效电源的内阻为6Ω，所以，当R₂=6Ω时，R₂上消耗的功率最大为1.5W。

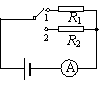例2：如图，电源的内阻不可忽略．已知定值电阻R₁=10Ω，R₂=8Ω．当电键S接位置1时，电流表的示数为0.20A．那么当电键S接位置2时，电流表的示数可能是下列的哪些值？

A.0.28A　　 B.0.25A　　 C.0.22A　　 D.0.19A

解：电键接2后，电路的总电阻减小，总电流一定增大，所以不可能是0.19A．电源的路端电压一定减小，原来路端电压为2V，所以电键接2后路端电压低于2V，因此电流一定小于0.25A．所以只能选C。

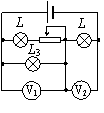例3：如图所示，电源电动势为E，内电阻为r．当滑动变阻器的

触片P从右端滑到左端时，发现电压表V₁、V₂示数变化的绝对值分

别为ΔU₁和ΔU₂，下列说法中正确的是

A.小灯泡L₁、L₃变暗，L₂变亮　　　

B.小灯泡L₃变暗，L₁、L₂变亮

C.ΔU₁<ΔU₂　　　　　　

D.ΔU₁>ΔU₂

解：滑动变阻器的触片P从右端滑到左端，总电阻减小，总电流增大，路端电压减小。与电阻蝉联串联的灯泡L₁、L₂电流增大，变亮，与电阻并联的灯泡L₃电压降低，变暗。U₁减小，U₂增大，而路端电压U= U₁+ U₂减小，所以U₁的变化量大于 U₂的变化量，选BD。

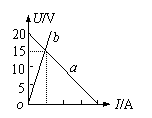
例4：如图所示，图线a是某一蓄电池组的伏安特性曲线，图线b是一只某种型号的定值电阻的伏安特性曲线．若已知该蓄电池组的内阻为2.0Ω，则这只定值电阻的阻值为______Ω。现有4只这种规格的定值电阻，可任意选取其中的若干只进行组合，作为该蓄电池组的外电路，则所组成的这些外电路中，输出功率最大时是_______W。

解：由图象可知蓄电池的电动势为20V，由斜率关系知外电阻阻值为6Ω。用3只这种电阻并联作为外电阻，外电阻等于2Ω，因此输出功率最大为50W。

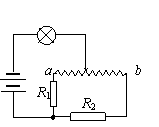
例5：如图所示，电路中ab是一段长10 cm，电阻为100Ω的均匀电阻丝。两只定值电阻的阻值分别为R₁=80Ω和R₂=20Ω。当滑动触头P从a端缓慢向b端移动的全过程中灯泡始终发光。则当移动距离为____cm时灯泡最亮，移动距离为_____cm时灯泡最暗。

解：当P移到右端时，外电路总电阻最小，灯最亮，这时aP长10cm。当aP间电阻为20Ω时，外电路总电阻最大，灯最暗，这时aP长2cm。

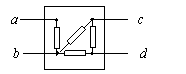
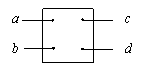例6：如图所示，黑盒有四个接线柱，内有4只阻值均为6Ω的电阻，每只电阻都直接与接线柱相连。测得R_ab=6Ω,R_ac=R_ad=10Ω。R_bc=R_bd=R_cd=4Ω,试画出黑盒内的电路。

解：由于最小电阻是R_bc=R_bd=R_cd=4Ω，只有2只6Ω串联后再与1只6Ω并联才能出现4Ω,因此bc、cd 、db间应各接1只电阻。再于ab间接1只电阻，结论正合适。

6.断路点的判定。

当由纯电阻组成的串联电路中仅有一处发生断路故障时，用电压表就可以方便地判定断路点：凡两端电压为零的用电器或导线是无故障的；两端电压等于电源电压的用电器或导线发生了断路。

5.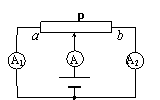滑动变阻器的两种特殊接法。

在电路图中，滑动变阻器有两种接法要特别引起重视：

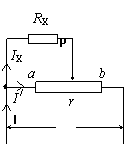⑴右图电路中，当滑动变阻器的滑动触头P从a端滑向b端的过程中，到达中点位置时外电阻最大，总电流最小。所以电流表A的示数先减小后增大；可以证明：A₁的示数一直减小，而A₂的示数一直增大。

⑵右图电路中，设路端电压U不变。当滑动变阻器的滑动触头P从a端滑向b端的过程中，总电阻逐渐减小；总电流I逐渐增大；R_X两端的电压逐渐增大，电流I_X也逐渐增大(这是实验中常用的分压电路的原理)；滑动变阻器r左半部的电流I ^/ 先减小后增大。

4.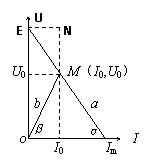闭合电路的U-I图象。

右图中a为电源的U-I图象；b为外电阻的U-I图象；两者的交点坐标表示该电阻接入电路时电路的总电流和路端电压；该点和原点之间的矩形的面积表示输出功率；a的斜率的绝对值表示内阻大小； b的斜率的绝对值表示外电阻的大小；当两个斜率相等时(即内、外电阻相等时图中矩形面积最大，即输出功率最大(可以看出当时路端电压是电动势的一半，电流是最大电流的一半)。

3.变化电路的讨论。

闭合电路中只要有一只电阻的阻值发生变化，就会影响整个电路，使总电路和每一部分的电流、电压都发生变化。讨论依据是：闭合电路欧姆定律、部分电路欧姆定律、串联电路的电压关系、并联电路的电流关系。以右图电路为例：设R₁增大，总电阻一定增大；由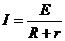，I一定减小；由U=E-Ir，U一定增大；因此U₄、I₄一定增大；由I₃= I-I₄，I₃、U₃一定减小；由U₂=U-U₃，U₂、I₂一定增大；由I₁=I₃ -I₂，I₁一定减小。总结规律如下：

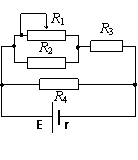①总电路上R增大时总电流I减小，路端电压U增大；

②变化电阻本身和总电路变化规律相同；

③和变化电阻有串联关系(通过变化电阻的电流也通过该电阻)的看电流(即总电流减小时，该电阻的电流、电压都减小)；

④和变化电阻有并联关系的(通过变化电阻的电流不通过该电阻)看电压(即路端电压增大时，该电阻的电流、电压都增大)。

2.电源的功率和效率。

⑴功率：①电源的功率(电源的总功率)P_E=EI

②电源的输出功率P_出=UI

③电源内部消耗的功率P_r=I ²r

⑵电源的效率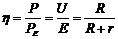：(最后一个等号只适用于纯电阻电路)

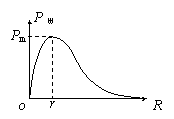电源的输出功率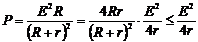，可见电源输出功率随外电阻变化的图线如图所示，而当内外电阻相等时，电源的输出功率最大，为。

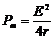目的要求

复习闭合电路的欧姆定律及其应用。

知识要点

1.主要物理量。

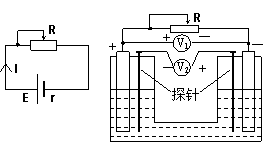研究闭合电路，主要物理量有E、r、R、I、U，前两个是常量，后三个是变量。闭合电路欧姆定律的表达形式有：

(1)E=U_外+U_内

(2)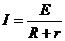 (I、R间关系)

(3)U=E-Ir(U、I间关系)

(4)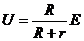(U、R间关系)

从(3)式看出：当外电路断开时(I = 0)，路端电压等于电动势。而这时用电压表去测量时，读数却应该略小于电动势(有微弱电流)。当外电路短路时(R = 0，因而U = 0)电流最大为I_m=E/r(一般不允许出现这种情况，会把电源烧坏)。

4.电路中有关电容器的计算。

⑴电容器跟与它并联的用电器的电压相等。

⑵在计算出电容器的带电量后，必须同时判定两板的极性，并标在图上。

⑶在充放电时，电容器两根引线上的电流方向总是相同的，所以要根据正极板电荷变化情况来判断电流方向。

⑷如果变化前后极板带电的电性相同，那么通过每根引线的电荷量等于始末状态电容器电荷量的差；如果变化前后极板带电的电性改变，那么通过每根引线的电荷量等于始末状态电容器电荷量之和。

例题分析

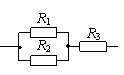例1：已知如图，R₁=6Ω，R₂=3Ω，R₃=4Ω，则接入电路后这三只电阻的实际功率之比为_________。

解：本题解法很多，注意灵活、巧妙。经过观察发现三只电阻的电流关系最简单：电流之比是I₁∶I₂∶I₃=1∶2∶3；还可以发现左面两只电阻并联后总阻值为2Ω，因此电压之比是U₁∶U₂∶U₃=1∶1∶2；在此基础上利用P=UI，得P₁∶P₂∶P₃=1∶2∶6

例2：已知如图，两只灯泡L₁、L₂分别标有“110V，60W”和“110V，100W”，另外有一只滑动变阻器R，将它们连接后接入220V的电路中，要求两灯泡都正常发光，并使整个电路消耗的总功率最小，应使用下面哪个电路？

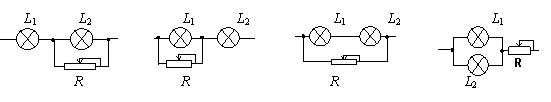A.　　　　　　　 B.　　　　　　　 C.　　　　　　 D.

解：A、C两图中灯泡不能正常发光。B、D中两灯泡都能正常发光，它们的特点是左右两部分的电流、电压都相同，因此消耗的电功率一定相等。可以直接看出：B图总功率为200W，D图总功率为320W，所以选B。

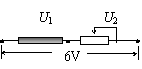例3：实验表明，通过某种金属氧化物制成的均匀棒中的电流I跟电压U之间遵循I =kU ³的规律，其中U表示棒两端的电势差，k=0.02A/V³。现将该棒与一个可变电阻器R串联在一起后，接在一个内阻可以忽略不计，电动势为6.0V的电源上。求：⑴当串联的可变电阻器阻值R多大时，电路中的电流为0.16A？⑵当串联的可变电阻器阻值R多大时，棒上消耗的电功率是电阻R上消耗电功率的1/5？

解：画出示意图如右。

⑴由I =kU ³和I=0.16A，可求得棒两端电压为2V，因此变阻器两端电压为4V，由欧姆定律得阻值为25Ω。

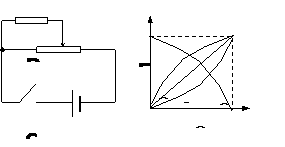⑵由于棒和变阻器是串联关系，电流相等，电压跟功率成正比，棒两端电压为1V，由I =kU³得电流为0.02A，变阻器两端电压为5V，因此电阻为250Ω。

例4：左图为分压器接法电路图，电源电动势为E，内阻不计，变阻器总电阻为r。闭合电键S后，负载电阻R两端的电压U随变阻器本身a、b两点间的阻值R_x变化的图线应最接近于右图中的哪条实线？

A.①　　 B.②　　　 C.③　　 D.④

解：当R_x增大时，左半部分总电阻增大，右半部分电阻减小，所以R两端的电压U应增大，排除④；如果没有并联R，电压均匀增大，图线将是②；实际上并联了R，对应于同一个R_x值，左半部分分得的电压将比原来小了，所以③正确，选C。

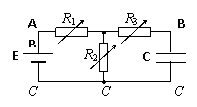例5：已知如图，电源内阻不计。为使电容器的带电量增大，可采取以下那些方法：

A.增大R₁　　 B.增大R₂

C.增大R₃　　 D.减小R₁

解：由于稳定后电容器相当于断路，因此R₃上无电流，电容器相当于和R₂并联。只有增大R₂或减小R₁才能增大电容器C两端的电压，从而增大其带电量。改变R₃不能改变电容器的带电量。因此选BD。

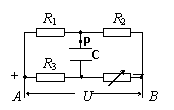
例6：已知如图，R₁=30Ω，R₂=15Ω，R₃=20Ω，AB间电压U=6V，A端为正C=2μF，为使电容器带电量达到Q =2×10^{- 6C}，应将R₄的阻值调节到多大？

解：由于R₁ 和R₂串联分压，可知R₁两端电压一定为4V，由电容器的电容知：为使C的带电量为2×10^-6C，其两端电压必须为1V，所以R₃的电压可以为3V或5V。因此R₄应调节到20Ω或4Ω。两次电容器上极板分别带负电和正电。

还可以得出：当R₄由20Ω逐渐减小的到4Ω的全过程中，通过图中P点的电荷量应该是4×10^-6C，电流方向为向下。