21．(本小题满分12分)若椭圆C的中心在坐标原点O，焦点在x轴上，过左焦点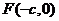的直线交椭圆C于P、Q两点，若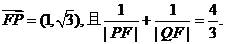

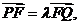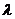　 (1)若求实数值；

　 (2)求椭圆C的方程。

20．(本小题满分12分)如图，四棱锥P-ABCD中，PB⊥底面ABCD，CD⊥PD，底面ABCD为直角梯形，AD‖BC，AB⊥BC，AB=AD=PB=3，点E在棱PA上，且PE=2EA。

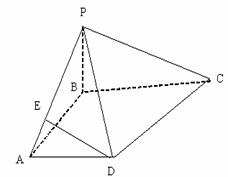　 (1)求异面直线PA与CD所成的角；

　 (2)求证：PC//平面EBD；

　 (3)求二面角A-BE-D的大小的余弦值。

19．(本小题满分12分)设数列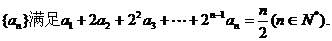

　 (1)求数列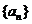的通项公式；

　 (2)设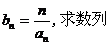

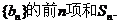
18．(本题满分12分)学校高三文科班、理科班各选出3名学生组成代表队进行乒乓球对抗赛，比赛规则是：①按“单打、双打、单打”的顺序进行比赛；②代表队中每名队员至少报名参加一盘比赛，至多参加两盘比赛，但不得参加两盘单打比赛；③先胜两盘的队获胜，比赛结束。若已知每盘比赛双方胜的概率均为。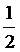

　　　 问：(1)文科班有多少种不同的排阵方式？

　 (2)文科班连胜两盘的概率是多少？

　 (3)文科班恰好胜一盘的概率是多少？

17．(本小题满分12分)在△ABC中，角A、B、C所对的边分别为a、b、c，且满足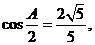

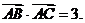
　 (I)求△ABC的面积；

　 (II)若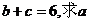的值。

16．已知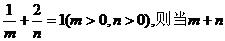取得最小值时，

椭圆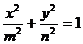的离心率是　　 　　　　　　　。

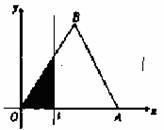
15．如图，△OAB是边长为2的正三角形，

记△OAB位于直线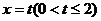左侧的图形的面积，

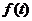则函数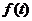的解析式为：　　 　　

14．已知P是椭圆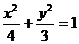上一点，F₁，F₂是焦点，=　　　 。

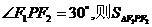13．从4个班级的学生中选出7名学生代表，若每一个班级中至少有一名代表，

则选法种数为　　　　　 。

12．已知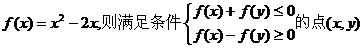所形成区域的面积为

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A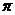．　　　　　　　　　　　 B．3　　　　　　　　　　　　 C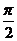．　　　　　　　　　　　 D．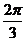

第Ⅱ卷(非选择题，共90分)