
18.解:(1)因为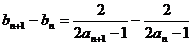 …………1分
…………1分
=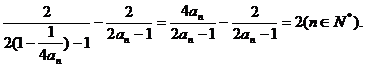
所以,数列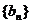 是等差数列.………………4分
是等差数列.………………4分
(2)因为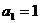 ,所以
,所以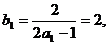 所以
所以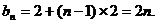
由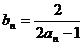 得,
得,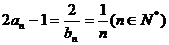 ,所以
,所以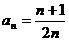 ,…………6分
,…………6分
所以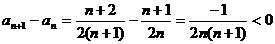 ,
,
所以在数列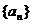 中对于任意的
中对于任意的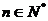 都有
都有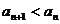 .………………8分
.………………8分
(3)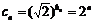 ,设
,设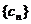 中存在三项
中存在三项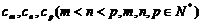 成等差数列
成等差数列
则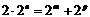 ,所以
,所以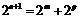 ,………9分
,………9分 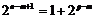 ,………11分
,………11分
因为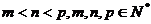 ,所以
,所以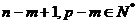 ,
,
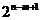 为偶数,
为偶数,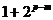 为奇数,所以
为奇数,所以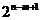 与
与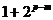 不可能相等,…………13分
不可能相等,…………13分
所以数列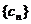 中不存在可以构成等差数列的三项.………………14分
中不存在可以构成等差数列的三项.………………14分
17.解:方法一(1)证明:连结AC交BD于点O ,连结OE,
,连结OE,
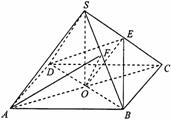 因为S-ABCD是正四棱锥,∴ABCD是正方形,所以O是AC的中点.
因为S-ABCD是正四棱锥,∴ABCD是正方形,所以O是AC的中点.
因为E是侧棱SC的中点, 所以OE//AS,…………2分
所以OE//AS,…………2分
又OE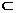 平面BDE,AS
平面BDE,AS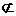 平面BDE,所以直线SA//平
平面BDE,所以直线SA//平
面BDE.…………4分
(2)解:因为AD//BC,异面直线SA和BC所 成角的大
成角的大
小是60° 所以∠SAD=60°…………6分
△SDA是等边三角形.
根据正棱锥的性质得,△SDC、△SBA、△SBC也是等边三角形.
连结SO,取SB中点F,连结AF、OF,因为O是正方形ABCD的中心,
根据正棱锥的性质得,SO⊥平面ABCD,∴AO⊥SO,又AO⊥BD,所以AO⊥平面SBD,……7分
因为SB⊥AF,根据三垂线定理的逆定理得,OF⊥SB,所以∠AFO是二面角A-SB-D的平面角.……………………9分
因为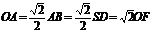 ,所以在RtAOF中,
,所以在RtAOF中,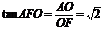 ,
,
即二面角A-SB-D的大小是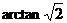 .…………10分
.…………10分
(3)解:因为E是侧棱SC的中点,所以BE⊥SC,DE⊥SC,所以SC⊥平面BDE,
∴平面SCB⊥平面BDE,过D作平面SCB的垂线,垂足在直线BE上,即BE为BD
在平面SCB上的射影,所以∠DBE为直线BD和平面SBC所成的角,…………12分
因为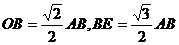 ,所以
,所以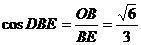 ,
,
所以直线BD和平面SBC所成的角的大小为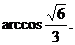 ………………14分
………………14分
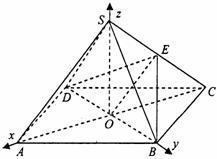
方法二:(1)证明:连AC交BD于点O,连结SO,OE. 根据正四棱锥的性质,得SO⊥面ABCD. 以OA、OB、OS所在射线分别作为非负x轴、非负y轴、非负z轴建立空间直角坐标系.…………1分
因为异面直线SA和BC所成角的大小是60°,AD//BC,所以∠SAD=60°,……2分
因而△SDA是等边三角形,根据正棱锥的性质,得△SDC,△SBA,△SBC也是等边三角形. 设AB=a,则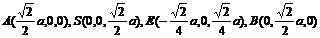 [来源:Z。X。X。K]
[来源:Z。X。X。K]
 因为
因为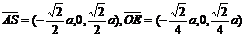 ,
,
所以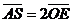 ,所以AS//OE.…………4分
,所以AS//OE.…………4分
又OE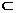 面BDE,AS
面BDE,AS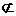 面BDE,
面BDE,
所以AS//面BDE.………5分
(2)设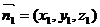 是平面S
是平面S AB的法向量.
AB的法向量.
则由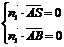 得
得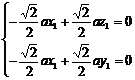 …………6分
…………6分
取x1=1,得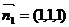 .…………7分
.…………7分
因为OA⊥SO,且OA⊥BD,所以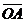 是平面SBD的法向量.
是平面SBD的法向量.
则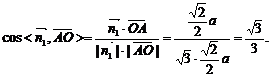 ……………
…………… …9分
…9分
所以二面角A-SB-D的大小是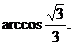 ………………10分
………………10分
(3 )设
)设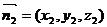 是平面SBC的法向量.
是平面SBC的法向量.
则由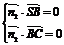 ,得
,得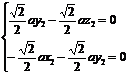 取
取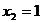 ,得
,得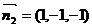 ,……12分
,……12分
又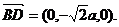 则
则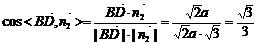 ,……13分
,……13分
设BD和平面SBC所成的角的大小为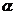 ,则
,则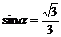 ,
,
即直线BD和平面SBC所成的角为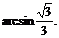 ………………14分
………………14分
16.①③④(注:全部选对得5分;选出错误选项②得0分;其余情况得2分)
11.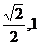 12.-160 13.(-2,-1) 14.乙种
15.8;6
12.-160 13.(-2,-1) 14.乙种
15.8;6 
1.B 2.A 3.C 4.B 5.A 6.D 7.A 8.B 9.B; 10.C;
18.在数列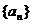 中,
中,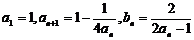 ,其中
,其中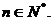
(1)求证:数列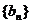 是等差数列;
是等差数列;
(2)求证:在数列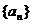 中对于任意的
中对于任意的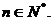 都有
都有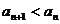 ;
;
(3)设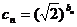 ,试问数列
,试问数列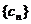 中是否存在三项它们可以构成等差数列?如果存在,求出这三项;如果不存在,请说明理由.
中是否存在三项它们可以构成等差数列?如果存在,求出这三项;如果不存在,请说明理由.
2010年 高考限时训练(7)答案
17.
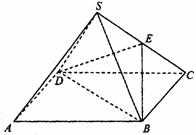 如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
如图,正四棱锥S-ABCD中,E是侧棱SC的中点,异面直线SA和BC所成角的大小是60°.
(1)求证:直线SA//平面BDE;
(2)求二面角A-SB-D的大小;
(3)求直线BD和平面SBC所成角的大小.
16.设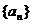 的公比为q的等比数列,其前n项的积为Tn,并且满足条件
的公比为q的等比数列,其前n项的积为Tn,并且满足条件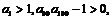
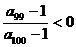 .给出下
.给出下 列结论:
列结论:
①0< q<1;②T198<1;③a99a101<1;使④Tn<1成立的最小自然数n等于199. 其中正确结论的编号是
q<1;②T198<1;③a99a101<1;使④Tn<1成立的最小自然数n等于199. 其中正确结论的编号是  .
.
15.设集合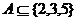 ,则集合A的个数为
;如果集合A中至多有一个奇数,则这样的集合A共有
个.
,则集合A的个数为
;如果集合A中至多有一个奇数,则这样的集合A共有
个.
14.甲、乙两种水稻连续5年的平均单位产量如下(单位:t/hm2):
|
品种 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
|
甲 |
9.4 |
9.8 |
10.8 |
9.7 |
10.3 |
|
乙 |
9.8 |
9.9 |
10 |
10.2 |
10.1 |
其中产量比较稳定的水稻品种是  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com