
2.设集合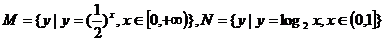 ,则集合
,则集合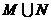 是
是
( )
A.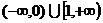 B.
B.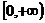 C.
C.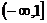 D.
D.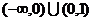
1.如果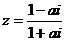 为纯虚数,则实数a等于 ( )
为纯虚数,则实数a等于 ( )
A.0 B.-1 C.1 D.-1或1
20.解:(I)由已知,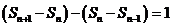 (
(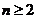 ,
,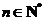 ), ………………2分
), ………………2分
即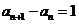 (
(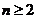 ,
,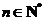 ),且
),且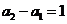 .
.
∴数列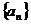 是以
是以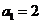 为首项,公差为1的等差数列.
为首项,公差为1的等差数列.
∴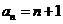 .……………………………………………………………………………4分
.……………………………………………………………………………4分
(II)∵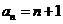 ,∴
,∴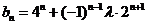 ,要使
,要使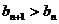 恒成立,
恒成立,
∴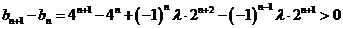 恒成立,
恒成立,
∴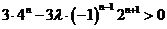 恒成立,
恒成立,
∴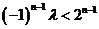 恒成立.……………………………………………………………6分
恒成立.……………………………………………………………6分
(ⅰ)当 为奇数时,即
为奇数时,即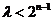 恒成立,…………………………………………7分
恒成立,…………………………………………7分
当且仅当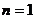 时,
时,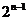 有最小值为1,
有最小值为1,
∴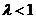 .………………………………………………………………………………9分
.………………………………………………………………………………9分
(ⅱ)当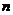 为偶数时,即
为偶数时,即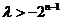 恒成立,………………………………………10分
恒成立,………………………………………10分
当且仅当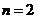 时,
时,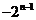 有最大值
有最大值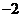 ,
,
∴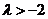 .……………………………………………………………………………12分
.……………………………………………………………………………12分
即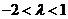 ,又
,又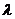 为非零整数,则
为非零整数,则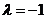 .
.
综上所述,存在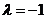 ,使得对任意
,使得对任意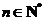 ,都有
,都有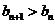 .…………………14分
.…………………14分
19.解:(Ⅰ)由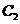 :
: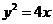 知
知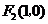 .……………………………………………1分
.……………………………………………1分
设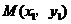 ,
,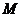 在
在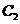 上,因为
上,因为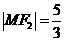 ,所以
,所以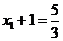 ,
,
得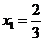 ,
,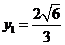 .………………………………………………………………… 3分
.………………………………………………………………… 3分
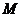 在
在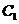 上,且椭圆
上,且椭圆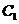 的半焦距
的半焦距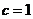 ,于是
,于是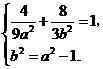 ………………………5分
………………………5分
消去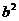 并整理得
并整理得 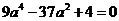 , 解得
, 解得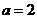 (
(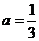 不合题意,舍去).
不合题意,舍去).
故椭圆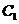 的方程为
的方程为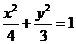 . ………………………………………………… 7分
. ………………………………………………… 7分
(Ⅱ)由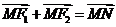 知四边形
知四边形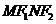 是平行四边形,其中心为坐标原点
是平行四边形,其中心为坐标原点 ,
,
因为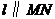 ,所以
,所以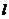 与
与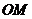 的斜率相同,
的斜率相同,
故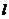 的斜率
的斜率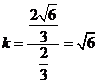 .
.
设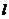 的方程为
的方程为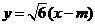 .……………………………………………………… 8分
.……………………………………………………… 8分
由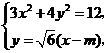 ………………………………………………………………… 9分
………………………………………………………………… 9分
消去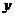 并化简得
并化简得 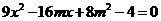 .…………………………………… 10分
.…………………………………… 10分
设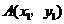 ,
,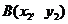 ,
,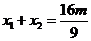 ,
,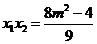 .……………………11分
.……………………11分
因为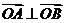 ,所以
,所以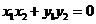 .
.
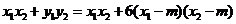
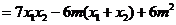
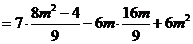
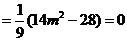 .……………… 12分
.……………… 12分
所以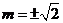 .此时
.此时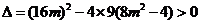 ,
,
故所求直线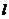 的方程为
的方程为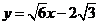 ,或
,或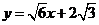 . …………………… 14分
. …………………… 14分
18.解:(Ⅰ)因为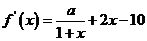 ………………………………………… 2分
………………………………………… 2分
所以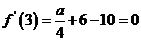
因此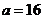 . ………………………………………………………………… 4分
. ………………………………………………………………… 4分
(Ⅱ)由(Ⅰ)知,
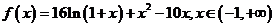
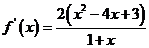 .………………………………………………………… 6分
.………………………………………………………… 6分
当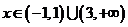 时,
时,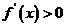 ;
;
当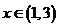 时,
时,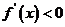 .
.
所以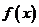 的单调增区间是
的单调增区间是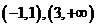 ;
;
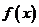 的单调减区间是.
的单调减区间是.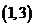 ……………………………………………………… 9分
……………………………………………………… 9分
(Ⅲ)由(Ⅱ)知,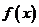 在
在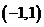 内单调增加,在
内单调增加,在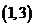 内单调减少,在
内单调减少,在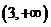 上单调增加,且当
上单调增加,且当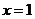 或
或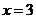 时,
时,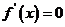 .……………………………………………… 10分
.……………………………………………… 10分
所以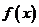 的极大值为
的极大值为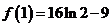 ,极小值为
,极小值为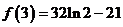 .……………12分
.……………12分
所以在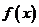 的三个单调区间
的三个单调区间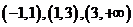 直线
直线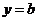 有
有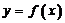 的图象各有一个交点,当且仅当
的图象各有一个交点,当且仅当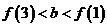 .
.
因此,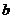 的取值范围为
的取值范围为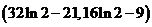 .……………………………………… 14分
.……………………………………… 14分
17.(I)由题意知,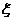 的可能取值为
的可能取值为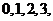 且
且
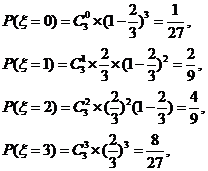
所以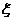 的分布列为
的分布列为
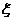
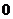
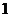
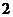
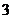
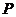
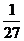
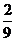
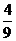

………………………………………………… 5分
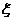 的数学期望为
的数学期望为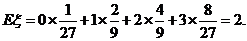 …………………………7分
…………………………7分
(II)用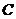 表示“甲得2分乙得1分”这一事件,用
表示“甲得2分乙得1分”这一事件,用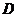 表示“甲得3分乙得0分”这一事件,
表示“甲得3分乙得0分”这一事件,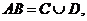
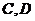 互斥.
互斥.
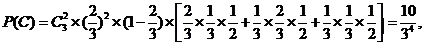 …………9分
…………9分
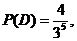 ………………………………………………………………………… 11分
………………………………………………………………………… 11分
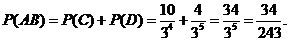 ………………………… 13分
………………………… 13分
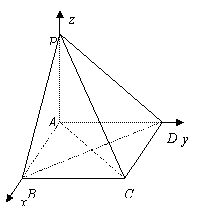
16.(Ⅰ)在Rt△BAD中,AD=2,BD=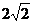 ,
,
∴AB=2,ABCD为正方形,因此BD⊥AC.
∵PA⊥平面ABCD,
∴BD⊥PA .
∵ ,
,
∴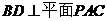 .………………………… 4分
.………………………… 4分
得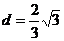 .
……………………………………………………………5分
.
……………………………………………………………5分
(Ⅱ)如图建立空间直角坐标系,则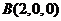 ,
,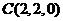 ,
,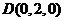 ,
,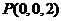
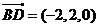 ,
,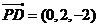 ,
,
易求平面 的法向量为
的法向量为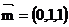 ,
,
平面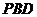 的法向量为
的法向量为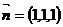 …………………………………………… 7分
…………………………………………… 7分
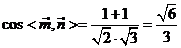 ,
,
二面角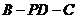 的余弦值
的余弦值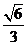 . …………………………………………… 9分
. …………………………………………… 9分
(III)因为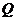 在
在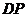 上,所以可设
上,所以可设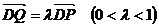 ,
,
又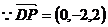 ,
,
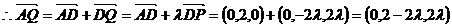
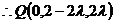 ,
,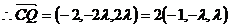 .……………………… 10分
.……………………… 10分
由(Ⅱ)可知平面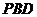 的法向量为
的法向量为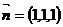 ,
,
所以设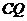 与平面
与平面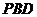 所成的角为
所成的角为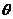 ,则有:
,则有:
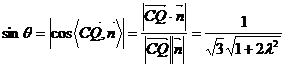 …………………………………… 11分
…………………………………… 11分
所以有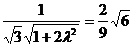 ,
,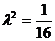 ,
,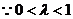 ,
, 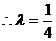 ………12分
………12分
所以存在且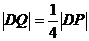 . ……………………………………………………………13分
. ……………………………………………………………13分
15.解:(I)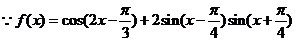
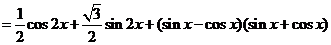
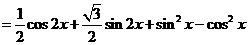
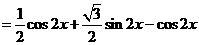
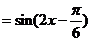 ………………………………………… 4分
………………………………………… 4分
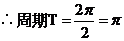 .……………………………………………6分
.……………………………………………6分
由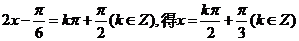
 函数图象的对称轴方程为
函数图象的对称轴方程为 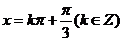 .…………… 8分
.…………… 8分
(II)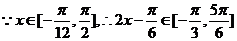 …………………………………
9分
…………………………………
9分
因为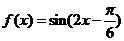 在区间
在区间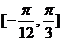 上单调递增,在区间
上单调递增,在区间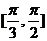 上单调递减,
上单调递减,
所以
当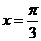 时,
时,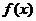 取最大值 1.
取最大值 1.
又 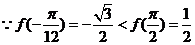 ,当
,当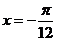 时,
时,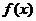 取得最小值
取得最小值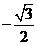 .
.
 所以 函数
所以 函数 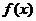 在区间
在区间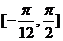 上的值域为
上的值域为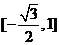 .……………………………12分
.……………………………12分
9.15 10.
9 11. 25 12. 1320 13.(0,2);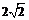 14. ①②
14. ①②
20. (本题满分14分)
已知数列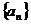 中,
中,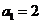 ,
,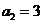 ,其前
,其前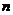 项和
项和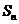 满足
满足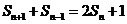 (
(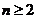 ,
,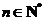 ).
).
(1)求数列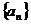 的通项公式;
的通项公式;
(2)设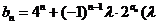 为非零整数,
为非零整数,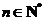 ),试确定
),试确定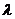 的值,使得对任意
的值,使得对任意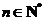 ,都有
,都有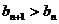 成立.
成立.
密云高中数学(理科)模拟答案及评分标准
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com