
20.(本小题满分12分)
已知数列{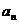 }的前n项和Sn=-
}的前n项和Sn=-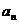 -
-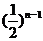 +2(n为正整数).
+2(n为正整数).
(I)令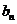 =
=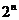
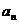 ,求证数列{
,求证数列{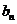 }是等差数列,并求数列{
}是等差数列,并求数列{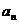 }的通项公式;
}的通项公式;
(Ⅱ)令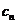 =
=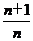
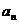 ,求Tn=c1+c2+…+cn.
,求Tn=c1+c2+…+cn.
19.(本小题满分12分)
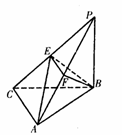 如图,三棱锥P-ABC中,PB⊥底面ABC,AC⊥BC,PB=BC=AC,点E、F分别是PC、PA的中点.
如图,三棱锥P-ABC中,PB⊥底面ABC,AC⊥BC,PB=BC=AC,点E、F分别是PC、PA的中点.
(I)求证:PC⊥平面BEF;
(Ⅱ)求二面角A-EB-F的大小.
18.(本小题满分12分)
甲、乙两队参加世博知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,
答错得零分.假设甲队每人答对的概率均为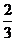 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为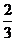 ,
,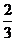 ,
,
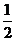 ,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.
(I)求随机变量ξ的分布列和数学期望;
(Ⅱ)用A表示“甲、乙两队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(A·B).
17.(本小题满分10分)
在△ABC中,角A、B、C所对的边分别是a、b、c,已知cosA=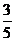 ,tan
,tan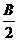 +cot
+cot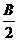 =
=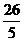 ,c=9
,c=9
(I)求tanB的值;
(Ⅱ)求△ABC的面积.
16.对于任意x∈R,不等式2x2-a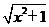 +3>0恒成立,则实数a的取值范围是_________________.
+3>0恒成立,则实数a的取值范围是_________________.
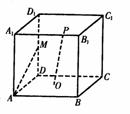
15.正方体ABCD-A1B1C1D1中,M为DD1的中点,O为正方
形ABCD的中心,P为梭A1B1上一点,则直线OP与AM
所成角的大小为________________.
14. 已知椭圆
已知椭圆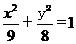 ,过左焦点F1的直线交椭圆于A,B两点,F2为右焦点,若|AF2|,
,过左焦点F1的直线交椭圆于A,B两点,F2为右焦点,若|AF2|,
|BF2|,|AB|成等差数列,则|BF2|=______________.
13.某项测量结果ξ服从正态分布N(1,σ2),(σ>0),若ξ在(0,1)内取值的概率为0.4,则ξ在(2,+∞)上取值的概率为_____________.
12.已知f(x)是定义在R上的奇函数,且f(x+2)=-f(x),当-1<x≤0时,f(x)=sinx,则使f(x)<0成立的x范围是
A.(2n-1,2n),n∈Z B.(4n-1,4n),n∈Z
C.(4n-2,4n-1),n∈Z D.(4n-2,4n),n∈Z
第Ⅱ卷(非选择题,共90分)
11.已知双曲线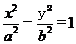 (a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的左支上,且|PF1|=
(a>0,b>0)的左、右焦点分别为F1,F2,点P在双曲线的左支上,且|PF1|=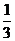 |PF2|,则双曲线离心率的最大值为
|PF2|,则双曲线离心率的最大值为
A.3
B.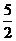 C.2
D.
C.2
D.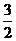
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com