
1. 证平行、证垂直
具体方法利用共线向量基本定理证明向量平行,再证线线、线面平行是证明平行问题的常用手段,由共面向量基本定理先证直线的方向向量与平面内不共线的两向量共面,再证方向向量上存在一点不属于平面,从而得到线面平行。
证明线线、线面垂直则可通过向量垂直来实现。
例1 如图1,E、F分别为空间四边形ABCD中AB、CD的中点,证明AD、EF、BC平行于同一平面。
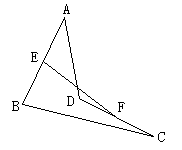
图1
证明: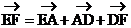 ,且
,且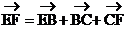
又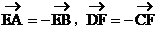
所以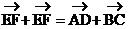
即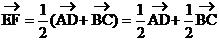
可知,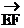 与
与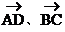 共面,所以EF与AD、BC平行于同一平面。
共面,所以EF与AD、BC平行于同一平面。
例2. 已知A(1,-2,11),B(4,2,3),C(6,-1,4),则ΔABC是___________。
分析: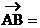 (3,4,-8),
(3,4,-8),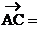 (5,1,-7),
(5,1,-7),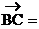 (2,-3,1)
(2,-3,1)
显见: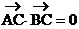 ,故ΔABC为直角三角形。
,故ΔABC为直角三角形。
3. 根据图象找相对应周期、振幅、初相。
|
年级 |
高中 |
学科 |
数学 |
版本 |
|
期数 |
|
||||||
|
内容标题 |
浅谈函数y=Asin(ωx+w) |
||||||||||||
|
分类索引号 |
G.622.46 |
分类索引描述 |
辅导与自学 |
||||||||||
|
主题词 |
浅谈函数y=Asin(ωx+w) |
栏目名称 |
专题辅导 |
||||||||||
|
供稿老师 |
|
审稿老师 |
|
||||||||||
|
录入 |
张玲 |
一校 |
胡丹 |
二校 |
|
审核 |
|
||||||
2. 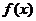 可化为
可化为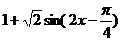
1. 原函数可化为
3. 如图为函数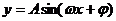 图象的一段,求其解析式。
图象的一段,求其解析式。
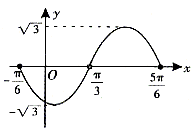
答案与提示:
2. 已知函数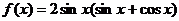 。
。
(1)求函数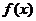 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数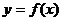 在区间
在区间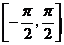 上的图象。
上的图象。
例4. 设函数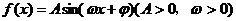 ,求:(1)
,求:(1)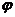 取何值时,
取何值时,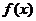 为奇函数;(2)
为奇函数;(2)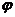 取何值时,
取何值时,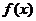 为偶函数。
为偶函数。
分析:考查三角函数的奇偶性。
解析:已知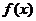 的定义域为R。
的定义域为R。
(1)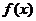 为奇函数
为奇函数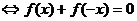
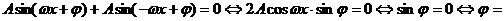
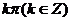 。
。
(2)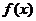 为偶数
为偶数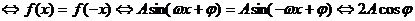
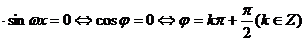 。
。
例5. 如果函数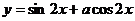 的图象关于直线
的图象关于直线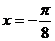 对称,则a=( )
对称,则a=( )
A. 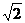 B.
B.
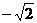 C.
1 D.
-1
C.
1 D.
-1
解法1: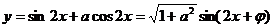 (其中
(其中 ),由题意知
),由题意知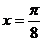 时,y应有最小值或最大值。故
时,y应有最小值或最大值。故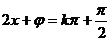 ,即
,即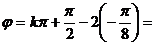
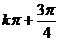 ,从而
,从而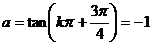 。
。
解法2: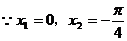 ,是定义域中关于
,是定义域中关于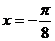 对称的两点,
对称的两点,
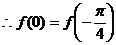 ,即
,即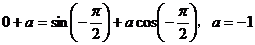 。
。
故答案为D。
练一练:
1. 已知函数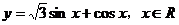 。
。
(1)当y取最大值时,求自变量x的取值集合;
(2)该函数的图象可由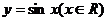 的图象经过怎样的平移和伸缩变换得到的?
的图象经过怎样的平移和伸缩变换得到的?
3. 变换图象求解析式
例3. 已知函数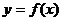 图象上每个点的纵坐标保持不变,将横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移
图象上每个点的纵坐标保持不变,将横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移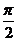 个单位,得到的曲线
个单位,得到的曲线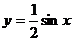 图象相同,则
图象相同,则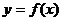 的函数表达式为( )
的函数表达式为( )
A. 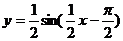 B.
B.
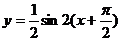
C. 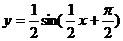 D.
D.
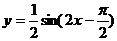
解析: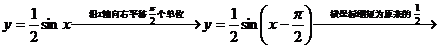
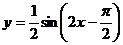 ,故答案为D。
,故答案为D。
总结:常用逆向思维的方式来解决此类题,这种思维方法在解决有些问题时起关键作用。
2. 由条件求解析式
例2. 若函数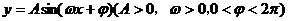 的最小值是-2,周期为
的最小值是-2,周期为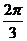 ,且它的图象过(0,
,且它的图象过(0,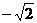 ),求其解析式。
),求其解析式。
解:由题意A=2,ω=3,故设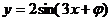
∵图象过(0,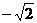 )
)
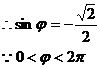
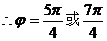
∴函数解析式为 或
或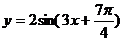 。
。
求解析式关键在于确定参数A、ω、j,其基本方法是在观察图象的基础上利用特定系数法,列方程求解。A:一般可由图象上的最大值或最小值来确定,即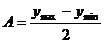 。ω:因为
。ω:因为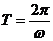 ,可结合图象,先求出周期T,相邻两个最高点(或两个最低点)的距离为T。j:即寻找“五点法”中第一个零值点(
,可结合图象,先求出周期T,相邻两个最高点(或两个最低点)的距离为T。j:即寻找“五点法”中第一个零值点(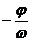 ,0)。
,0)。
对于函数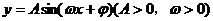 来说,其中A叫振幅,
来说,其中A叫振幅,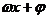 叫相位,w叫初相,
叫相位,w叫初相,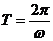 叫周期。
叫周期。
1. 由图象求解析式
例1. 已知函数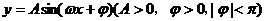 的图象如下图所示,试确定其解析式。
的图象如下图所示,试确定其解析式。
解:易知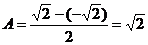
又由图象可知:
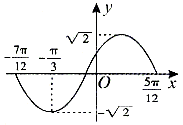
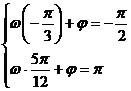 ,解得
,解得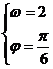
故所求解析式为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com