
4.设函数f(x)=log2x的反函数为y=g(x),若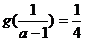 ,则a等于 ( )
,则a等于 ( )
A.-2 B.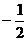 C.
C.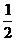 D.2
D.2
3.集合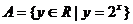 ,
,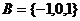 ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A.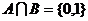 B.
B.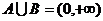
C.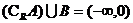 D.
D.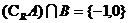
2.命题“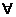 x>0,x2+x>O"的否定是 ( )
x>0,x2+x>O"的否定是 ( )
A.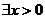 ,使得
,使得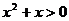 B.
B.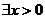 ,
,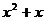 ≤0
≤0
C.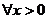 ,都有
,都有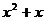 ≤0 D.
≤0 D.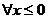 ,都有
,都有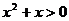
1.函数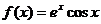 的图象在点(0,f(0))处的切线的倾斜角为 ( )
的图象在点(0,f(0))处的切线的倾斜角为 ( )
A.0 B.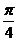 C.1 D.
C.1 D.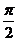
21.(13分)已知椭圆C的两个焦点为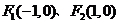 ,离心率
,离心率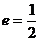 .
.
(1)求椭圆C的方程;
(2)若直线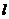 :
: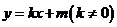 与椭圆交于不同的两点
与椭圆交于不同的两点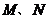 (
(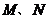 不是左、右顶点),且以
不是左、右顶点),且以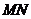 为直径的圆经过椭圆的右顶点
为直径的圆经过椭圆的右顶点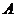 .求证:直线
.求证:直线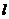 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
长沙地区四县(市)2010届高三统一考试试卷
20.(13分)设数列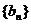 的前
的前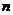 项和为
项和为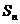 ,且
,且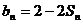 ;数列
;数列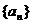 为等差数列,且a5=14,a7=20.
为等差数列,且a5=14,a7=20.
(1)求数列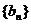 的通项公式;
的通项公式;
(2)若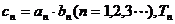 为数列
为数列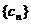 的前
的前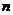 项和,求证:
项和,求证: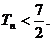
19.(13分)为了保护环境,发展低碳经济,某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本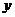 (元)与月处理量
(元)与月处理量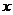 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: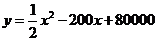 ,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴
多少元才能使该单位不亏损?
18.(12分)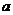 从
从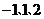 中任取一个数,b从
中任取一个数,b从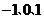 中任取一个数.
中任取一个数.
(I)求函数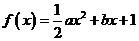 有零点的概率;
有零点的概率;
(II)求使两个不同向量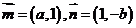 的夹角
的夹角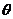 为锐角的概率.
为锐角的概率.
17、(12分)如图,已知多面体ABC-DEFG中,AB、AC、AD两两互相垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
(1)试判断CF是否与平面ABED平行?并说明理由;
(2)求多面体ABC-DEFG的体积.
16.(12分)已知函数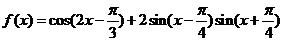
(1)求函数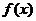 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
 (2)求函数
(2)求函数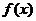 在区间
在区间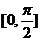 上的值域.
上的值域.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com