
18.(本小题满分13分)
某运动项目设置了难度不同的甲、乙两个系列,每个系列都有K和D两个动作.比赛时每位运动员自选一个系列完成,两个运作得分之和为该运动员的成绩.
假设每个运动员完全每个系列中的两个动作的得分是相互独立的.根据赛前训练统计数据,某运动员完成甲系列和乙系列的情况如下表:
表1:甲系列 表2:乙系列
现该运动员最后一个出场,之前其运动员的最高得分为115分.
(I)若该运动员希望获得该项目的第一名,应选择哪个系列?说明理由,并求其获得第一名的概率;
(II)若该运动员选择乙系列,求其成绩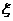 的分布列及其数学期望
的分布列及其数学期望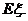
17.(本小题满分13分)
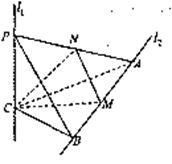
如图,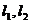 是两条互相垂直的异面直线,点P、C在直线
是两条互相垂直的异面直线,点P、C在直线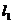 上,点A、B在直线
上,点A、B在直线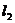
上,M、N分别是线段AB、AP的中点,且PC=AC=a,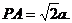
(I)证明: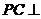 平面ABC;
平面ABC;
(II)设平面MNC与平面PBC所成的角为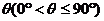
现给出四个条件:
①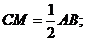 ②
②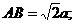 ③CM
③CM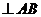 ④
④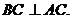
请从中再选择两上条件以确定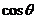 的值,并求之.
的值,并求之.
16.(本小题满分13分)
已知函数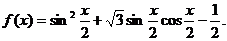
(I)求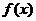 的单调递增区间;
的单调递增区间;
(II)将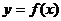 的图象向左平移
的图象向左平移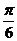 个单位,得到函数
个单位,得到函数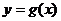 的图象.若
的图象.若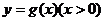 的图象与直线
的图象与直线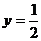 交点的横坐标由小到大依次是
交点的横坐标由小到大依次是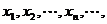 求数
求数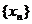 的前2n项的和.
的前2n项的和.
15.考察等式:
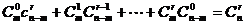 (*)
(*)
其中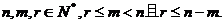
某同学用概率论方法证明等式(*)如下:
设一批产品共有n件,其中m件是次品,其余为正品.现从中随机抽出r件产品,
记事件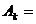 {取到的r件产品中恰好有k件次品},
{取到的r件产品中恰好有k件次品},
则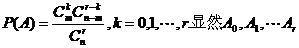 为互斥事件,且
为互斥事件,且
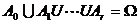 (必然事件),因此
(必然事件),因此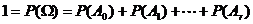 =
=
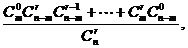 所以
所以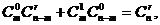 即等式(*)成立.
即等式(*)成立.
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
①等式(*)成立; ②等式(*)不成立;
③证明正确; ④证明不正确.
试写出所有正确判断的序号 .
14.已知抛物线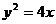 在焦点为F,过F且垂直于x轴的直线交该抛物线于A、B两点.若椭圆
在焦点为F,过F且垂直于x轴的直线交该抛物线于A、B两点.若椭圆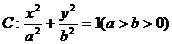 的右焦点与点F重合,右顶点与A、B构成等腰直角感触形,则椭圆C的离心率为
.
的右焦点与点F重合,右顶点与A、B构成等腰直角感触形,则椭圆C的离心率为
.
13.若x,y满足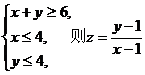 的最大值是
.
的最大值是
.
12.在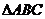 中,角A、B、C所对的边分别是a、b、c,若c=2,b=2a,且
中,角A、B、C所对的边分别是a、b、c,若c=2,b=2a,且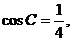 则a=
.
则a=
.
11.已知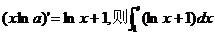 =
.
=
.
10.已知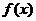 是定义在[a、b]上的函数,其图象是一条连续不断的曲线,且满足下列条件:
是定义在[a、b]上的函数,其图象是一条连续不断的曲线,且满足下列条件:
①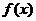 的值域为G,且
的值域为G,且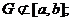
②对任意不同的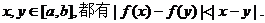
那么关于x的方程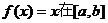 上的根的情况是 ( )
上的根的情况是 ( )
A.没有实数根 B.有且只有一个实数极
C.恰有两个不同的实数根 D.有无数个不同的实数根
第Ⅱ卷(非选择题,共100分)
9.今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量,当甲、乙两人为一方,丙、丁两人为另一方时,双方势均力敌;当甲与丙对调以后,甲、丁一方轻而易举地战胜了乙、丙一方;而乙凭其一人之力便战胜了甲、丙两人的组合.那么,甲、乙、丙、丁四人的“体力”由强到弱的顺序是 ( )
A.丁、乙、甲、丙 B.乙、丁、甲、丙
C.丁、乙、丙、甲 D.乙、丁、丙、甲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com