
2、填空
①.本诗选自《白玉·苦瓜》作者是著名诗人 余光中 ,1928年生于南京,现居台湾。
②.后来啊 乡愁是一方矮矮的坟墓 我在外头 母亲在里头 。
③.抒发对故国思念深情的诗句是:而现在/乡愁是一湾浅浅的海峡/我在这头/大陆在那头
3反复诵读课文,回答:(1)诗歌乡愁是通过哪些物体表现出来的?这样写有什么好处?
诗人巧妙的将“乡愁”这种感情进行了物化,把它分别寄托在“邮票”、“船票”、“坟墓”、“海峡”具体可感对象上,形成诗的意象,从而增加诗的艺术感染力
(2)课文内容前后排列的顺序能否调整?说说自己的理由。
“邮票”、“船票”、“坟墓”、“海峡”四个对象分别是人生四个阶级“乡愁”的对应物,这四个阶段分别是:小时候--长大后--后来--现在。小时候诗人少小离家,与母亲的书信往来,乡愁寄托在邮票上;长大后为生活而奔波,与爱人合合离离,乡愁寄托在船票上;到后来,母亲的一方坟墓将我与母亲永远分开了!而现在浅浅的海峡又把自己与祖国大陆分开了。个人的故乡之思上升到一群人的家国之思了
1、结合诗意解释下列词语
乡愁: 乡愁:对故乡的思念之情
海峡: 陆地间相对狭窄的海面
一方: 一堆
1、独在异乡为异客,每逢佳节倍思亲。 2、日暮乡关何处是,烟波江上使人愁。 3、乡书何处达,归雁洛阳边; 4、春风又绿江南岸,明月何时照我还; 5、露从今夜白,月是故乡明; 6、此夜曲中闻折柳,何人不起故园情; 7、共看明月应垂泪,一夜乡心五处同; 8、夕阳西下,断肠人在天涯; 9、浊酒一杯家万里,燕然未勒归无计; 10、应怜故乡水,万里送行舟。
1作者介绍:余光中:中国台湾诗人。福建永春人。先后在金陵大学(现南京大学)和厦门大学外文系学习。历任《蓝星》、《现代文学》等杂志的主编,著有长诗《天狼星》、诗集《蓝色的羽毛》、《天国夜市》等。此外尚有散文集、评论集多种。
2、表现乡愁的诗句:
4、 [巩固]C;5、 [巩固] ②③
2、 [巩固]-1,[提高]在同一坐标系内画函数y=3-x,y=lgx,y=10x的图象,交点为A、B,A、B关于直线y=x对称,得x1=3-x2;3、 [巩固] g(x)= x2-ax+3a在区间[2,+∞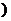 上递增且g(x)= x2-ax+3a>0在区间[2,+∞
上递增且g(x)= x2-ax+3a>0在区间[2,+∞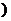 上恒成立,即a≤4且g(2)>0得-4<a≤4;
上恒成立,即a≤4且g(2)>0得-4<a≤4;
5.函数y=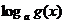 ,(
,(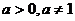 )的值域主要取决于g(x)。如:0<g(x)≤4,则
)的值域主要取决于g(x)。如:0<g(x)≤4,则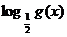 ∈[-2,+
∈[-2,+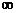 ),其中0<g(x)只是保证对数值存在的,并不限制对数值的范围。若g(x)无最(极)大值(即上无界),则函数y=
),其中0<g(x)只是保证对数值存在的,并不限制对数值的范围。若g(x)无最(极)大值(即上无界),则函数y=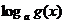 ,(
,(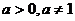 )的值域为R
)的值域为R g(x)min≤0(特别地:当g(x)是二次项系数为正的二次函数时g(x)min≤0
g(x)min≤0(特别地:当g(x)是二次项系数为正的二次函数时g(x)min≤0 ⊿≥0); 函数y=
⊿≥0); 函数y=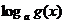 有最值
有最值 g(x)min≥0。
g(x)min≥0。
[举例] 函数y=log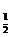 (2x2-2x+1)的值域为
。
(2x2-2x+1)的值域为
。
解析:2x2-2x+1=2(x-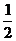 )2+
)2+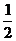 ≥
≥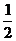 , log
, log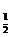 (2x2-2x+1)≤1,∴函数值域为(-
(2x2-2x+1)≤1,∴函数值域为(-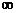 ,1
,1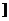 。
。
[巩固] 设函数f(x)=lg(x2+ax-a-1),给出下列命题:①f(x)有最小值;②当a=0时,f(x)值域为R;③当a>0时,在[2,+∞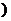 上有反函数;④若f(x)在区间[2,+∞
上有反函数;④若f(x)在区间[2,+∞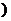 上单调递增,则实数a的取值范围是a≥-4.其中正确命题的序号是_____________
上单调递增,则实数a的取值范围是a≥-4.其中正确命题的序号是_____________
简答
4.函数y=ax的值域为(0,+ )。特别关注函数y=ax的值与1的大小,函数y=
)。特别关注函数y=ax的值与1的大小,函数y=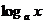 的值与0的大小。
的值与0的大小。
[举例1] 函数y=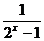 的值域是( )
的值域是( )
(A)(-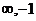 )
(B)(-
)
(B)(-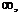 0)
0)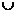 (0,+
(0,+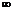 )
)
(C)(-1,+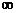 )
(D)(-
)
(D)(-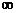 ,-1)
,-1)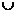 (0,+
(0,+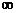 )
)
解析:思路一:“逆求”: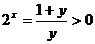 得:
得: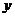 >0或
>0或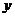 <-1,选D。思路二:
<-1,选D。思路二: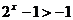 ,“取倒数”要特别注意不等式两边同号,若-1<
,“取倒数”要特别注意不等式两边同号,若-1<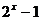 <0,则
<0,则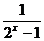 <-1;若
<-1;若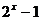 >0,则
>0,则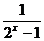 >0,综上,选D。
>0,综上,选D。
[举例2] .若logm9<logn9<0,那么m,n满足的条件是( )
(A)m>n>1 (B)n>m>1 (C)0<n<m<1 (D)0<m<n<1
解析:logm9与logn9底数不同,比较大小不甚方便,注意到logm9=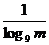 ,则由
,则由
logm9<logn9<0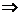
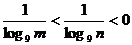
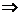 log9n<log9m<0
log9n<log9m<0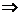 0<n<m<1,选C。
0<n<m<1,选C。
[巩固] 已知g(x)=loga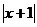 (a>0且a
(a>0且a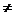 1)在(-1,0)上有g(x)>0,则f(x)=a
1)在(-1,0)上有g(x)>0,则f(x)=a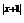 是( )
是( )
(A)在(-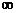 ,0)上的增函数
(B)在(-
,0)上的增函数
(B)在(-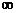 ,0)上的减函数
,0)上的减函数
(C)在(-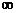 ,-1)上的增函数 (D)在(-
,-1)上的增函数 (D)在(-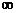 ,-1)上的减函数
,-1)上的减函数
3.关注对数函数的定义域,特别是在解对数不等式(留意对数变形的等价性)和研究对数函数的单调性(函数有意义才谈得上增减)时。
[举例1]函数f(x)的图像与函数g(x)=(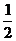 )x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
)x的图像关于直线y=x对称,则f(2x-x2)的单调减区间为( )
(A)(0,1) (B)[1,+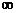 ] (C)(-
] (C)(-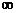 ,1) (D)[1,2]
,1) (D)[1,2]
解析:f(x)与g(x)互为反函数,即f(x)=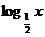 , f(2x-x2)=
, f(2x-x2)= 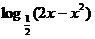 ,记h(x)=2x-x2,
,记h(x)=2x-x2,
则h(x)递增(“外层”递减)且h(x)>0(真数),∴x∈(0,1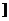 ,故选A。(在函数定义域内区间的“开”“闭”不影响函数的单调性,所以求函数单调区间时一般用开区间比较“稳妥”)。
,故选A。(在函数定义域内区间的“开”“闭”不影响函数的单调性,所以求函数单调区间时一般用开区间比较“稳妥”)。
[举例2]已知命题p: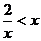 ;命题q:
;命题q: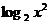 >1;则命题p是命题q的: ( )
>1;则命题p是命题q的: ( )
A.充分不必要条件,B.必要不充分条件,
C.充要条件 D.既不必要也不充分条件
解析:命题p: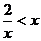 ,移项通分得:
,移项通分得: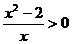 ,“序轴标根”得:
,“序轴标根”得: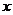 ∈
∈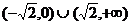 ,
,
命题q: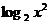 >1等价于:
>1等价于: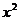 >2,即
>2,即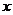 ∈
∈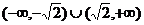 (注意:不等式
(注意:不等式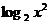 >1与不等式:2
>1与不等式:2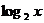 >1不等价,
>1不等价,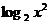 >1等价于2
>1等价于2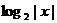 >1);从集合包含关系更容易看清两个命题的逻辑关系,选D。
>1);从集合包含关系更容易看清两个命题的逻辑关系,选D。
[巩固]已知函数f(x)=log2(x2-ax+3a)在区间[2,+∞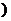 上递增,则实数a的取值范围是 。
上递增,则实数a的取值范围是 。
2.指数函数y=ax与对数函数y=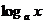 ,(
,(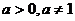 )是互为反函数即
)是互为反函数即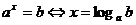 它是实现指数式与对数式相互转换的桥梁。当a>1时,两个函数在定义域内都递增;当0<a<1时,两个函数在定义域内都递减。
它是实现指数式与对数式相互转换的桥梁。当a>1时,两个函数在定义域内都递增;当0<a<1时,两个函数在定义域内都递减。
[举例1]光线透过一块玻璃板,其强度要减弱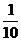 ,要使光线的强度减弱到原来的
,要使光线的强度减弱到原来的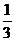 以下,至少需要这样的玻璃板 块。(参考数据:lg2=0.3010,lg3=0.4771)
以下,至少需要这样的玻璃板 块。(参考数据:lg2=0.3010,lg3=0.4771)
解析:记光线原来的强度为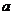 ,透过一块玻璃板后其强度变为
,透过一块玻璃板后其强度变为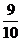
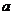 ,透过
,透过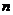 块玻璃板后其强度变为:
块玻璃板后其强度变为: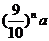 ,则
,则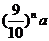 <
<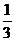
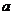 ,即
,即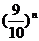 <
<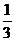 ,
,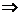
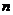 (2lg3-1)<-lg3
(2lg3-1)<-lg3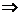
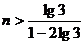 ≈10.4,(注意:2lg3-1<0),∴
≈10.4,(注意:2lg3-1<0),∴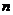 =11.
=11.
[举例2] loga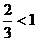 ,则a的取值范围是( )
,则a的取值范围是( )
(A)(0,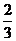 )
) (1,+
(1,+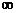 )
(B)(
)
(B)(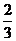 ,+
,+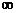 )
)
(C)(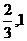 )
(D)(0,
)
(D)(0,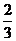 )
) (
(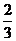 ,+
,+ )
)
解析:若a>1,则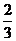 <a,∴a>1;若0<a<1,则
<a,∴a>1;若0<a<1,则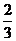 >a, ∴0<a<
>a, ∴0<a<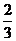 ;综上,选A。(本题中视1为logaa是化“数”为“对数”的通法)。
;综上,选A。(本题中视1为logaa是化“数”为“对数”的通法)。
[巩固] 若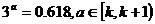 ,
,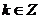 ,则
,则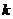 =__________。
=__________。
[提高] 方程x+lgx=3,x+10x=3的解分别为x1,x2,则x1+x2=____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com