
20.(本小题满分12分)
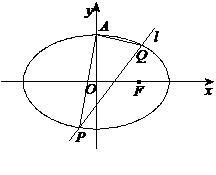 如图,已知椭圆
如图,已知椭圆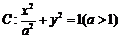 的上顶点为
的上顶点为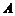 ,右焦点为
,右焦点为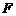 ,直线
,直线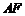 与圆
与圆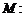
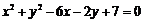 相切.
相切.
(Ⅰ)求椭圆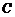 的方程;
的方程;
(Ⅱ)若不过点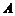 的动直线
的动直线 与椭圆
与椭圆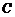 相
相
交于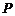 、
、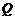 两点,且
两点,且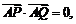 求证:直
求证:直
线 过定点,并求出该定点
过定点,并求出该定点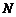 的坐标.
的坐标.
19.(本小题满分12分)
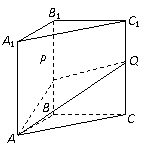
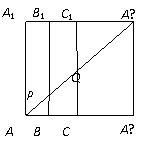
如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC-A1B1C1,在三棱柱ABC-A1B1C1中,
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比;
(Ⅲ)求面PQA与面ABC所成的锐二面角的余弦值.
18.(本小题满分12分)
为了解《中华人民共和国交通法》在学生中的普及情况,对某校6名学生进行问卷调查, 6人得分情况如下:5,6,7,8,9,10 ,把这6名学生的得分看成一个总体.
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
17.(本题满分12分)在ΔABC中,角A、B、C所对的边分别为a、b、c,且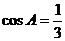 .
.
(Ⅰ)求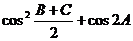 的值;
的值;
(Ⅱ)若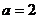 ,
,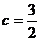 ,求∠C和ΔABC的面积.
,求∠C和ΔABC的面积.
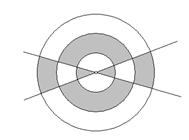
16.如图三同心圆, 其半径分别为3、2、1. 已知
图中阴影区域的面积是非阴影区域面积的 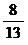 .则两直线所夹锐角的弧度 为
.
.则两直线所夹锐角的弧度 为
.
15.已知x、y满足约束条件 x≥-2 ,则z=(x+3)2+y2的最小值为 .
x+y ≥15.
14.设有一回归直线方程为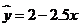 ,则变量
,则变量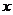 增加一个单位时,
增加一个单位时,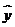 平均减少__________个单位.
平均减少__________个单位.
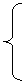 y≥0
y≥0
13.为了了解高三学生的身体状况.抽取了部分
男生的体重,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12.则抽取的男生人数是 .
12.函数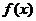 的定义域为
的定义域为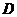 ,若对于任意
,若对于任意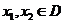 ,当
,当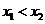 时,都有
时,都有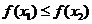 ,则称函数
,则称函数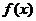 在
在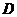 上为非减函数,设函数
上为非减函数,设函数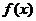 在
在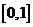 上为非减函数,且满足以下三个条件:①
上为非减函数,且满足以下三个条件:①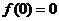 ;②
;②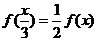 ;③
;③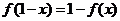 .则
.则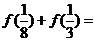 ( )
( )
A.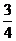 B.
B.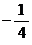 C.0 D.
C.0 D.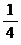
第Ⅱ卷(非选择题,共90分)
11.把一颗骰子投掷两次,观察出现的点数,记第一次出现点数为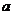 ,第二次出现点数为
,第二次出现点数为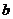 ,则方程组
,则方程组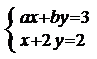 只有一个解的概率为
( )
只有一个解的概率为
( )
A.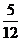 B.
B.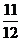 C.
C. D.
D.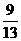
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com