
6. [巩固]B,
4. [巩固] C, [迁移]B,5. [举例]-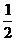 ,[巩固]
,[巩固]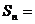
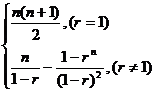
1. [巩固]C,[迁移]视Sn为关于n的二次函数,其图象是经过原点的抛物线上的点,故选B,2. [巩固]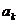 =
=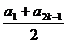 =
=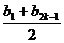 ≥
≥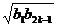 =
=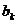 ,
,
[迁移]等比数列中奇数项的符号相同,偶数项的符号也相同;-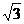 ,
,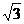 ,±
,±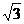 ,
,
[提高] Sn-Sn-5=an+an-1+an-2+an-3+an-4=55,与a1+a2+a3+a4+a5=25两式相加得5(a1+an)=80,得n=8,3.[巩固]6;
6.解等差(比)数列有关通项、求和问题时别忘了“基本元”,即把问题转化为首项a1,公差d(或公比q)的方程(组)或不等式(组)去处理。已知等差或等比数列中的任两项也可用 am-an=(m-n)d,或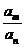 =qm-n。
=qm-n。
[举例1] 等差数列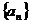 的前n项和Sn,若S3=9,S13=26求S23的值。
的前n项和Sn,若S3=9,S13=26求S23的值。
解析:用求和公式解方程组,求出a1,d,再代入求和公式中求S23,这是通法。也可简化为:
S3=3a2=9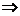 a2=3,S13=13a7=26
a2=3,S13=13a7=26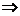 a7=2, ∴a12=
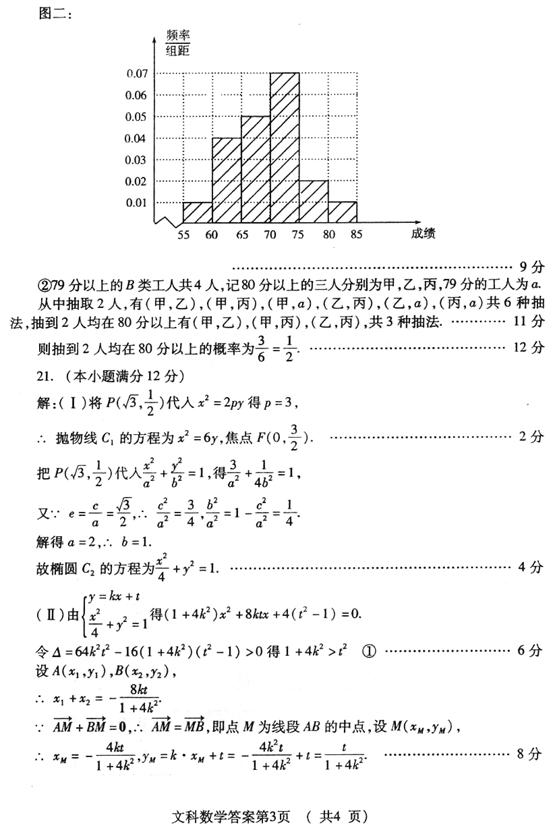
1(a2、a7、a12成等差数列),S23=23a12=23。
a7=2, ∴a12=
1(a2、a7、a12成等差数列),S23=23a12=23。
[举例2]已知等差数列{an}中,a3与a5的等差中项等于2,又a4与a6的等比中项等于6,则a10等于 (A) 54 (B) 50 (C) 26 (D) 16
解析:a3与a5的等差中项等于2,即a4=2;a4与a6的等比中项等于6,即a6=18;于是2d=16,
a10= a6+4d=50,选B。
[巩固]]已知等差数列{an}的首项a1=120,公差d=-4,若Sn≤an(n>1),则n的最小值为
(A)61 (B)62 (C)63 (D)70
[迁移]等差数列{an}中若am=n,an=m且m≠n求证:am+n=0;
简答
5.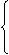 注意:等比数列求和公式是一个分段函数 na1
(q=1)
注意:等比数列求和公式是一个分段函数 na1
(q=1)
Sn= 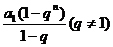
则涉及到等比数列求和时若公比不是具体数值须分类讨论解题。
[举例]已知等比数列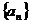 的公比为q,前n项和为Sn,且S3 ,S9 ,S6 成等差数列,求q3的值。
的公比为q,前n项和为Sn,且S3 ,S9 ,S6 成等差数列,求q3的值。
解析:不可直接用等比数列的求和公式,需讨论:若q=1,S3=3a1 ,S9=9a1,S6=6a1,则有:
18a1=3a1+6a1, 则a1=0, 与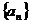 是等比数列矛盾,∴q≠1,于是有:
是等比数列矛盾,∴q≠1,于是有:
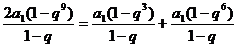 ,化简得:
,化简得: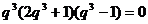 ,∴
,∴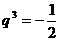 。
。
本题还可以用:第一个三项和、第二个三项和、第三个三项和成等比数列解决,留读者自己完成。
[巩固]已知an=1+r+r2+r3+…rn-1,则数列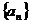 的前n项和
的前n项和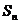 =______________
=______________
4. 等差数列当首项a1>0且公差d<0,前n项和存在最大值。利用不等式组: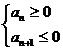
确定n值,即可求得Sn的最大值。等差数列当首项a1<0且公差d>0时,前n项和存在最小值。 类似地确定n值,即可求得sn的最小值;也可视sn为关于n的二次函数,通过配方求最值;还可以利用二次函数的图象来求。
[举例] 设等差数列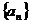 满足3 a8=5a13,且a1>0,则
满足3 a8=5a13,且a1>0,则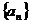 的前__________项和最大
的前__________项和最大
解析:思路一:由3 a8=5a13得:d=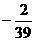 a1,若前n项和最大,则
a1,若前n项和最大,则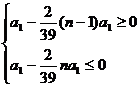 ,
,
又a1>0得: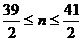 ,∴n=20,即
,∴n=20,即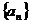 的前20项和最大。这一做法最通行。
的前20项和最大。这一做法最通行。
思路二:Sn=na1+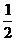 n(n-1)d=na1-
n(n-1)d=na1-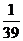 n(n-1)a1=-
n(n-1)a1=-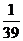 a1(n2-40n),当且仅当n=20时Sn最大。这一做法突显了数列的函数特征。思路三:由3 a8=5a13得15a8=25a13,即S15=S25,又∵a1>0,
a1(n2-40n),当且仅当n=20时Sn最大。这一做法突显了数列的函数特征。思路三:由3 a8=5a13得15a8=25a13,即S15=S25,又∵a1>0,
∴Sn的图象是开口向下的抛物线上的点列,对称轴恰为n=20,故n=20时Sn最大。这一做法中几乎没有运算,但设计太过“精妙”,非对等差数列的性质融会贯通而不能为,仅供欣赏。
[巩固] 数列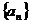 是等差数列,
是等差数列,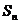 是其前n项和,且S5<S6,S6=S7>S8,则下列结论错误的是:A.d <0
B.a7=0 C.S9>S5
D. S6 ,S7均为
是其前n项和,且S5<S6,S6=S7>S8,则下列结论错误的是:A.d <0
B.a7=0 C.S9>S5
D. S6 ,S7均为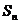 的最大值 ( )
的最大值 ( )
[迁移] 在等差数列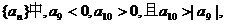 则在前n项和Sn中最大的负数为
则在前n项和Sn中最大的负数为
A.S16 B.S17 C.S18 D.S19 ( )
3.等差数列前n项和、次n项和、再后n项和(即连续相等项的和)仍成等差数列;等比数列前n项和(和不为0)、次n项和、再后n项和仍成等比数列。
[举例1]在等比数列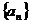 中,S2 =40,S4 =60,则S6等于
( )
中,S2 =40,S4 =60,则S6等于
( )
A 10 B 70 C 80 D 90
解析:在等比数列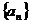 中,第一个两项和为40,第二个两项和为20(注意:S4是前4项和,不是两项和),则第三个两项和为10,S6为三个两项和相加,选B。
中,第一个两项和为40,第二个两项和为20(注意:S4是前4项和,不是两项和),则第三个两项和为10,S6为三个两项和相加,选B。
[举例2] 在等差数列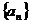 中,前n项之和为
中,前n项之和为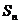 ,已知S3=4,S18-S15=12,则S18=
,已知S3=4,S18-S15=12,则S18=
解析:在等差数列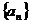 中,第一个三项和为4,第六个三项和为12,S18即首项为4,末项为12的等差数列的6项和,为48。
中,第一个三项和为4,第六个三项和为12,S18即首项为4,末项为12的等差数列的6项和,为48。
[巩固]在等差数列{an}中,其前n项和为Sn,已知S5=2-b,S10=4-b,则S15=_________
2. 等差数列{an}中,m+n=p+q,则am+an=ap+aq,等比数列{an}中,m+n=p+q,则aman=ap·aq(m、n、p、q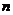 ∈
∈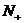 );等差(等比)数列中简化运算的技巧多源于这条性质。
);等差(等比)数列中简化运算的技巧多源于这条性质。
[举例1]在等差数列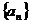 中,
中,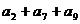 为常数,则其前( )项和也为常数
为常数,则其前( )项和也为常数
(A)6 (B)7 (C)11 (D)12
解析:等差数列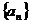 的前k项和为常数即
的前k项和为常数即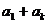 为常数,而
为常数,而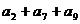 =3
=3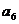 为常数,
为常数,
∴2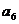 =
=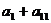 为常数,即前11项和为常数,选C。注意:千万不要以为
为常数,即前11项和为常数,选C。注意:千万不要以为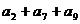 =
=
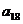 =
=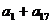 ,那就大错特错了!所谓“下标和相等则对应项的和相等”,是指两项和等于两项和,三项和等于三项和……。等差数列中“n项和”与“两项和(转化为a1+an)”有关,某一项或某几项和均需转化为“两项和”才能与“n项和”联系起来。
,那就大错特错了!所谓“下标和相等则对应项的和相等”,是指两项和等于两项和,三项和等于三项和……。等差数列中“n项和”与“两项和(转化为a1+an)”有关,某一项或某几项和均需转化为“两项和”才能与“n项和”联系起来。
[举例2]等比数列{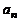 }中,a4+a6=3,则a5(a3+2a5+a7)=
}中,a4+a6=3,则a5(a3+2a5+a7)=
解析:a5(a3+2a5+a7)=a5a3+2a52+a5a7=a42+2a4a6+a62=(a4+a6)2=9
[巩固] 在正项的等差数列{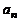 }和正项的等比数列{
}和正项的等比数列{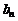 }中,有
}中,有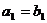 ,
,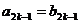 ,试比较
,试比较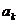 与
与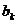 的大小。
的大小。
[迁移] 等比数列{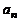 }中,
}中,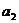 、
、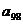 是方程
是方程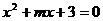 (
(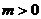 )的两根,则
)的两根,则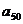 =
=
若把条件中的“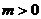 ”换成“
”换成“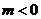 ”呢?若把条件中的“
”呢?若把条件中的“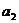 、
、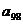 ”换成“
”换成“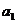 、
、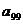 ”
”
呢?
[提高] 在等差数列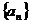 中,前n项之和为
中,前n项之和为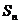 ,已知S5=25,Sn=64,Sn-5=9,则 n=_____
,已知S5=25,Sn=64,Sn-5=9,则 n=_____
1.公差不为0的等差数列的通项是关于n的一次函数,一次项系数是公差;前n项和是关于n的二次函数,二次项系数是公差之半且常数项为0;即等差数列{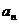 }中,
}中,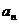 =
=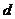
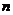 +
+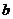 (
(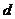 为公差,
为公差,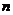 ∈
∈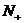 ),
),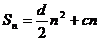 (
(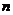 ∈
∈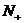 )。证明某数列是等差(比)数列,通常利用等差(比)数列的定义加以证明,即证:an-an-1=常数(
)。证明某数列是等差(比)数列,通常利用等差(比)数列的定义加以证明,即证:an-an-1=常数(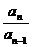 =常数) (
=常数) (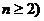 ,也可以证明连续三项成等差(比)数列。
,也可以证明连续三项成等差(比)数列。
[举例] {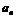 }、{
}、{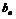 }都是各项为正的数列,对任意的
}都是各项为正的数列,对任意的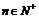 ,都有
,都有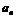 、
、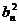 、
、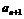 成等差数列,
成等差数列,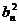 、
、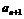 、
、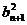 成等比数列.试问{
成等比数列.试问{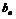 }是否为等差数列,为什么?
}是否为等差数列,为什么?
解析:由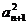 =
=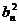
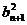 得
得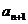 =
=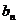
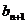 ,于是
,于是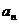 =
=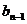
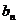 (
(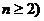 ,又2
,又2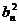 =
=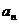 +
+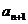 ,
,
∴2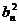 =
=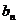
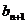 +
+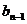
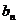 (
(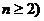 ,即2
,即2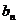 =
=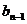 +
+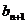 (
(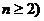 ,∴数列{
,∴数列{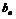 }是等差数列。
}是等差数列。
注意:当用定义证明等差(比)数列受阻时,别忘了这“一招”!上述思路的关键是由“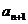 =
=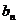
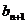 ”到“
”到“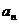 =
=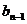
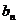 (
(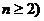 ”的过渡,即所谓“升降标”,这也是处理数列问题的一个通法。
”的过渡,即所谓“升降标”,这也是处理数列问题的一个通法。
[巩固]已知等差数列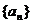 的前
的前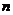 项和为
项和为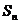 ,且
,且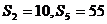 ,则过两点
,则过两点
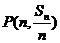 、
、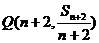 的直线的斜率为:
的直线的斜率为:
(A)4 (B)3 (C) 2 (D)1
[迁移]公差非零的等差数列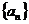 中,前n项之和为 中,前n项之和为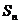 ,则数列 ,则数列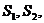 … …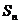 …中 …中
|
||
|
A.不存在等于零的项 |
B.最多有一项等于零 |
|
C.最多有2项等于零 D.可有2项以上等于零
22.(本题满分14分)
已知实数a≥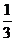 ,函数y=ex-ax区间[-ln3,o)上的增函数,设函数f(x)=ax3-
,函数y=ex-ax区间[-ln3,o)上的增函数,设函数f(x)=ax3-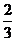 x
x 
(I)求a的值并写出g(x)的表达式;
(Ⅱ)求证:当x>o时,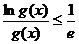 ;
;
 (Ⅲ).
(Ⅲ).



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com