
4.已知某闭花授粉植物(2n=28)高茎(D)对矮茎(d)为显性,在♀DD×♂dd杂交中,若D基因所在的同源染色体在减数第一次分裂时不分离,产生的雌配子染色体数目及在这种情况下杂交后代的株高表现型分别为 ( )
A.13或15 高茎或矮茎 B.14 高茎或矮茎
C.13或15 高茎 D.14 高茎
3.下列对处于不同免疫状态的小鼠分析合理的是 ( )
A.吞噬细胞缺陷的小鼠特异性免疫无法产生
B.胸腺被破坏的小鼠因无淋巴因子产生,无体液免疫
C.骨髓被破坏的小鼠输入造血干细胞后能恢复体液免疫和细胞免疫
D.B细胞缺陷的小鼠虽无法合成抗体,但仍能对结核杆菌产生免疫反应
2.下列关于基因工程中运载体的叙述不正确的是 ( )
A.目的基因导入受体细胞后,受体细胞即发生基因突变
B.目的基因与运载体结合的过程发生在细胞外
C.运载体对宿主细胞的生理代谢不起作用
D.常用的运载体有质粒、噬菌体和动植物病毒等
1.右图表示大豆种子的形成和萌发过程,据图分析,正确的叙述是 ( )
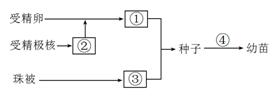
A.④过程中①的干重不断增加
B.④过程初期需要添加必需矿质元素
C.①到幼苗过程细胞中核DNA的种类不变,RNA不同
D.若③中细胞的基因型为EeFf,则②中细胞的基因型为EeeFff
9、 (Ⅰ)由已知,设f1(x)=ax2,由f1(1)=1,得a=1, ∴f1(x)= x2.设f2(x)=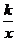 (k>0),它的图象与直线y=x的交点分别为A(
(k>0),它的图象与直线y=x的交点分别为A(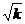 ,
,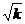 ),B(-
),B(-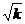 ,-
,-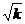 )
)
由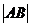 =8,得k=8,. ∴f2(x)=
=8,得k=8,. ∴f2(x)=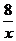 .故f(x)=x2+
.故f(x)=x2+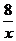 .
.
(Ⅱ) (证法一)f(x)=f(a),得x2+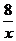 =a2+
=a2+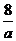 ,
,
即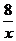 =-x2+a2+
=-x2+a2+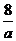 .在同一坐标系内作出f2(x)=
.在同一坐标系内作出f2(x)=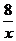 和
和
f3(x)= -x2+a2+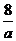 的大致图象,其中f2(x)的图象是以坐
的大致图象,其中f2(x)的图象是以坐
标轴为渐近线,且位于第一、三象限的双曲线, f3(x)与的图象是以(0, a2+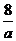 )为顶点,开口向下的抛物线.因此, f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.又∵f2(2)=4, f3(2)= -4+a2+
)为顶点,开口向下的抛物线.因此, f2(x)与f3(x)的图象在第三象限有一个交点,即f(x)=f(a)有一个负数解.又∵f2(2)=4, f3(2)= -4+a2+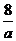 ,当a>3时,. f3(2)-f2(2)= a2+
,当a>3时,. f3(2)-f2(2)= a2+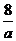 -8>0,当a>3时,在第一象限f3(x)的图象上存在一点(2,f(2))在f2(x)图象的上方.f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.因此,方程f(x)=f(a)有三个实数解.
-8>0,当a>3时,在第一象限f3(x)的图象上存在一点(2,f(2))在f2(x)图象的上方.f2(x)与f3(x)的图象在第一象限有两个交点,即f(x)=f(a)有两个正数解.因此,方程f(x)=f(a)有三个实数解.
(证法二)由f(x)=f(a),得x2+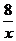 =a2+
=a2+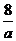 ,即(x-a)(x+a-
,即(x-a)(x+a- )=0,得方程的一个解x1=a.方程x+a-
)=0,得方程的一个解x1=a.方程x+a- =0化为ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2=
=0化为ax2+a2x-8=0,由a>3,△=a4+32a>0,得x2=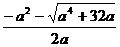 , x3=
, x3=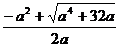 ,x2<0, x3>0, ∵x1≠ x2,且x2≠
x3.若x1= x3,即a=
,x2<0, x3>0, ∵x1≠ x2,且x2≠
x3.若x1= x3,即a=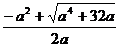 ,则3a2=
,则3a2=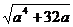 , a4=4a,得a=0或a=
, a4=4a,得a=0或a=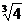 ,这与a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三个实数解.
,这与a>3矛盾,∴x1≠ x3.故原方程f(x)=f(a)有三个实数解.
8、(Ⅰ)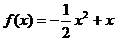 。(Ⅱ)存在m=-4,n=0满足要求。
。(Ⅱ)存在m=-4,n=0满足要求。
7、(Ⅰ)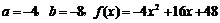
(Ⅱ)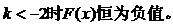
5、6 6、[-5/4,1]
例1. 解:令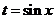 ,
,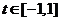 ,
,
∴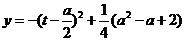 ,对称轴为
,对称轴为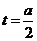 ,
,
(1)当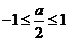 ,即
,即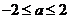 时,
时,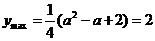 ,得
,得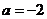 或
或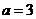 (舍去).
(舍去).
(2)当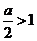 ,即
,即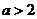 时,函数
时,函数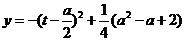 在
在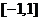 单调递增,
单调递增,
由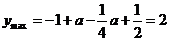 ,得
,得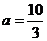 .
.
(3)当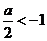 ,即
,即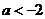 时,函数
时,函数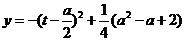 在
在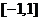 单调递减,
单调递减,
由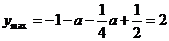 ,得
,得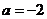 (舍去).
(舍去).
综上可得: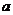 的值为
的值为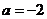 或
或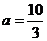 .
.
例2. 解法一:由题知关于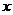 的方程
的方程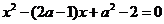 至少有一个非负实根,设根为
至少有一个非负实根,设根为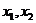
则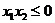 或
或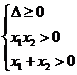 ,得
,得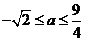 .
.
解法二:由题知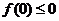 或
或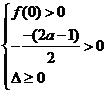 ,得
,得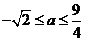 .
.
例3.
解:(1)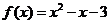 ,
,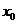 是
是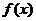 的不动点,则
的不动点,则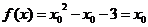 ,得
,得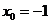 或
或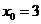 ,函数
,函数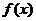 的不动点为
的不动点为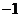 和
和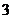 .
.
(2)∵函数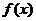 恒有两个相异的不动点,∴
恒有两个相异的不动点,∴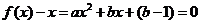 恒有两个不等的实根,
恒有两个不等的实根,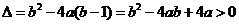 对
对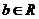 恒成立,
恒成立,
∴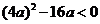 ,得
,得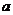 的取值范围为
的取值范围为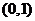 .
.
(3)由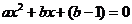 得
得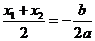 ,由题知
,由题知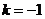 ,
,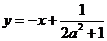 ,
,
设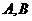 中点为
中点为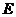 ,则
,则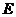 的横坐标为
的横坐标为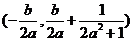 ,∴
,∴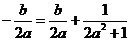 ,
,
∴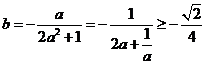 ,当且仅当
,当且仅当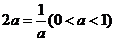 ,即
,即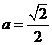 时等号成立,
时等号成立,
∴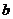 的最小值为
的最小值为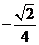 .
.
冲刺强化训练(1)
1、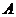 2、A 3、C 4、
2、A 3、C 4、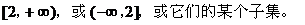
1、D 2 110 3、D 4、(-∞,-1)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com