
1.讨论二次函数的区间最值问题:①注意对称轴与区间的相对位置;②函数在此区间上的单调性;
例1.已知函数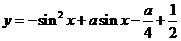 的最大值为
的最大值为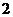 ,求
,求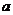 的值 .
的值 .
例2. 已知函数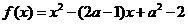 与非负
与非负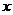 轴至少有一个交点,求
轴至少有一个交点,求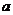 的取值范围.
的取值范围.
例3.对于函数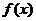 ,若存在
,若存在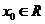 ,使
,使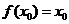 ,则称
,则称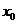 是
是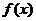 的一个不动点,已知函数
的一个不动点,已知函数
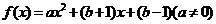 ,
,
(1)当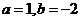 时,求函数
时,求函数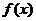 的不动点;
的不动点;
(2)对任意实数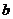 ,函数
,函数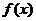 恒有两个相异的不动点,求
恒有两个相异的不动点,求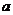 的取值范围;
的取值范围;
(3)在(2)的条件下,若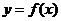 的图象上
的图象上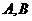 两点的横坐标是
两点的横坐标是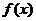 的不动点,且
的不动点,且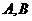 两点关于直线
两点关于直线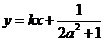 对称,求
对称,求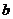 的最小值.
的最小值.
4、已知方程x2+2px+1=0有一个根大于1,有一个根小于1,则P的取值为 。
3、函数f(x)=x4-2x2+2的单调增区间是( )
(A)[1,+∞), (B)(-∞,-1)∪[1,+∞), (C)[-1,0]∪[1,+∞), (D)以上都不对
2、 已知f(x)=x2+(lga+2)x+lgb且f(-1)=-2,又f(x)≥2x对一切x∈R都成立,求a+b
= .
1、 f(x)是定义在全体实数上的偶函数,它的图象关于x=2为轴对称,已知当x∈(-2,2)时f(x)的表达式为-x2+1,则当x∈(-6,-2)时,f(x)的表达式是: ( )
(A)-x2+1 (B)-(x-2)2+1 (C)-(x+2)2+1 (D)-(x+4)2+1
2.体会数形结合及函数与方程的数学思想方法.
1.准确理解函数的有关概念.
26.(本题满分12分)如图所示, 在平面直角坐标系xoy中, 矩形OABC的边长OA、OC分别为12cm、6cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=ax2+bx+c经过点A、B, 且18a+c=0.
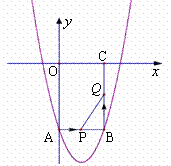 (1)求抛物线的解析式.
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动, 同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时, 设△PBQ的面积为S, 试写出S与t之间的函数关系式, 并写出t的取值范围.
②当S取得最大值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是平行四边形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
25.(本题满分10分)如图所示,以RtΔABC的直角边AB为直径作圆O,与斜边交于点D,E为BC边上的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)连接OE、AE,当∠CAB为何值时,四边形AOED是平行四边形?并在此条件下求
sin∠CAE的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com