
下表是世界某著名城市1961-1990年部分气候资料,据此回答3-4题:
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
降雨量(毫米) |
15.0 |
17.0 |
20.0 |
41.0 |
69.0 |
93.0 |
82.0 |
77.0 |
40.0 |
30.0 |
14.0 |
17.0 |
|
降雨日数 |
5.5 |
4.6 |
4.8 |
8.3 |
11.4 |
13.3 |
11.8 |
13.7 |
10.4 |
8.7 |
4.9 |
6.2 |
|
日平均日照(小时) |
10.9 |
10.6 |
9.4 |
7.8 |
6.6 |
5.8 |
6.2 |
6.8 |
7.5 |
9.0 |
10.3 |
10.8 |
3.该城市所属的气候类型主要分布在( )
A.赤道地区 B.大陆内部 C.大陆东岸 D.大陆西岸
4.该城市所处自然带的典型植被类型是( )
A.热带雨林 B.亚寒带针叶林
C.亚热带常绿硬叶林 D.亚热带常绿阔叶林
读地球表面某区域的经纬网图,M、N、P、Q四点位于相同半球。据图回答1-2题:
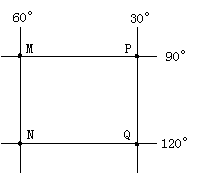
1.若图中P点位于世界某大河河口附近,则一架飞机从M点起飞,沿最短的航线到达N点,那么飞机飞行的方向是( )
A.一直向南 B.先西北再西南 C.先东北再东南 D.一直向北
2.若图上四点中只有Q点位于某大陆上,而其余三点均位于海洋,则下列关于四点的叙述正确的是( )
A.P、Q两点的实地距离与P、M两点间距离相等
B.Q点所在国家独占一个大陆,且濒临三大洋
C.P、M、N所在大洋北部锰结核储量最为丰富
D.当Q点区时为8点时,全球新一日和旧一日的范围刚好相等
4.[巩固]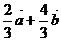 ,[迁移](1)2,(2)x2+y2+xy-1=0
,[迁移](1)2,(2)x2+y2+xy-1=0
1.[巩固]记: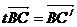 (B、C、C/共线),则
(B、C、C/共线),则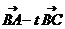 =
=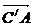 ∴|
∴|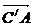 |≥|
|≥|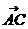 |即对直线BC上任意一点C/都有|A C/|≥|AC|∴AC ⊥BC,故选C;[迁移] |
|即对直线BC上任意一点C/都有|A C/|≥|AC|∴AC ⊥BC,故选C;[迁移] |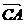 |=
|=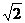 ,∴A点在以C为圆心,
,∴A点在以C为圆心,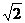 为半径的圆上,图示,选D, 2、[巩固](1)
为半径的圆上,图示,选D, 2、[巩固](1)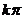 ,(2)
,(2) -
- = (sin
= (sin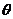 ,1-cos
,1-cos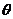 ),tan
),tan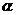 =
=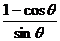 =tan
=tan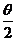 ,
,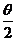 ∈(0,
∈(0,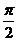 );[迁移]记⊿ABC中BC边上的高为
);[迁移]记⊿ABC中BC边上的高为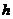 ,则|
,则|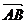 |sinB=|
|sinB=|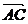 |sinC=
|sinC=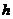 ,
,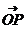 =
=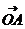 +
+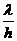 (
(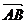 +
+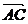 ),记BC的中点为M,
),记BC的中点为M, 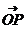 =
=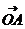 +2
+2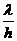
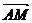 ,选C;3、 [巩固1]C,[巩固2] (1)
,选C;3、 [巩固1]C,[巩固2] (1)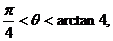 (2)以
(2)以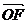 为x轴正向,O为原点建系,
为x轴正向,O为原点建系,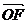 =(c,0),记Q(x0,y0),
=(c,0),记Q(x0,y0),
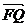 =(x0-c,y0),则:c(x0-c )=1,且
=(x0-c,y0),则:c(x0-c )=1,且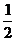 c|y0|=
c|y0|=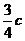 ,得:x0=
,得:x0=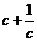 ,|y0|=
,|y0|=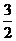 ,∴|
,∴|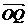 |2=
|2=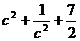 记:t=
记:t=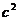 ,(t≥4),g(t)=
,(t≥4),g(t)=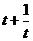 在[4,
在[4,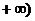 递增,∴当t=4即c=2,x0=
递增,∴当t=4即c=2,x0=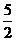 时,|
时,|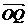 |最小,此时Q(
|最小,此时Q(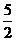 ,±
,±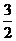 ),Q在椭圆上且c=2,求得椭圆方程:
),Q在椭圆上且c=2,求得椭圆方程: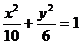 ;
;
[迁移] (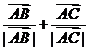 )·=0,即角A的平分线垂直于BC,∴ AB=AC,又
)·=0,即角A的平分线垂直于BC,∴ AB=AC,又
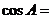
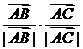 = ∴∠A=
= ∴∠A=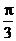 ,所以△ABC为等边三角形,选A。
,所以△ABC为等边三角形,选A。
4.关注平面向量基本定理中的关键词:…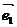 、
、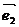 不共线…有且仅有一对实数
不共线…有且仅有一对实数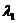 、
、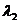 …。
…。
[举例] 设同一平面内的两向量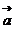 、
、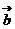 不共线,
不共线, 是该平面内的任一向量,则关于x的方程
是该平面内的任一向量,则关于x的方程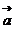 x2+
x2+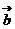 x+
x+ =
= 的解的情况,下列叙述正确的是:( )
的解的情况,下列叙述正确的是:( )
A.至少有一个实数解 B.至多有一个实数解
C.有且只有一个实数解 D.可能有无数个解
解析:此题不可用“判别式”,“判别式”只能判别实系数一元二次方程的根的情况,而本题中二次方程的系数是向量。原方程即:  =- x2
=- x2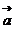 - x
- x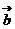 ,∵
,∵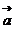 、
、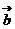 不共线,可视为“基底”,
不共线,可视为“基底”,
根据平面向量基本定理知,有且仅有一对实数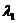 、
、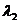 使得
使得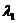 = - x2且
= - x2且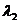 = - x,即当
= - x,即当
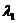 = -
= -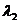 2时方程有一解,否则方程无解,故选B。
2时方程有一解,否则方程无解,故选B。
[巩固]已知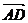 、
、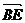 分别是⊿ABC的边BC、AC上的中线,且
分别是⊿ABC的边BC、AC上的中线,且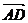 =
=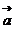 ,
,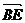 =
=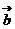 ,则
,则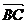 可以用向量
可以用向量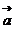 、
、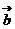 表示为
。
表示为
。
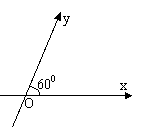 [迁移]如图,在平面斜坐标系
[迁移]如图,在平面斜坐标系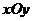 中,∠
中,∠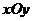 =600,平面上任
=600,平面上任
一点P关于斜坐标系的斜坐标是这样定义的:若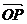 =x
=x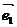 +y
+y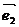 ,
,
其中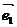 、
、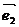 分别为与x轴、y轴同方向的单位向量,则P点的
分别为与x轴、y轴同方向的单位向量,则P点的
斜坐标为(x,y).
(1)若点P的斜坐标为(2,-2),求P到O的距离|PO|;(2)求以O为圆心、1为半径的圆在斜坐标系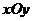 中的方程。
中的方程。
简答
3.向量的数量积: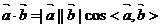 (符号运算);其中
(符号运算);其中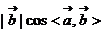 可视为向量
可视为向量  在向量
在向量  上的射影。向量的数量积是数而不是向量,向量的射影是数而未必是正数。。向量的数量积满足交换率、对加(减)法的分配率、不满足结合率,即(
上的射影。向量的数量积是数而不是向量,向量的射影是数而未必是正数。。向量的数量积满足交换率、对加(减)法的分配率、不满足结合率,即( ·
· )·
)·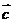 ≠
≠ ·(
·( ·
·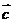 ),一个等式的两边、一个分式的分子分母不能同乘以或同除以一个向量。若
),一个等式的两边、一个分式的分子分母不能同乘以或同除以一个向量。若 =(x1,y1),
=(x1,y1),  =(x2,y2),则
=(x2,y2),则 ·
· = x1 x2+y1 y2(坐标运算);在使用向量数量积的公式时,要根据题目的条件和设问特点选择使用符号运算还是坐标运算。
= x1 x2+y1 y2(坐标运算);在使用向量数量积的公式时,要根据题目的条件和设问特点选择使用符号运算还是坐标运算。
应用:(1)角度: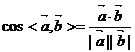 且
且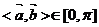 ;
;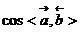 可视为与
可视为与 、
、 同向的两个单位向量的数量积;<
同向的两个单位向量的数量积;< ,
, >为锐角
>为锐角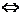

 >0且
>0且 、
、 不共线,<
不共线,< ,
, >为锐角
>为锐角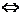

 >0且
>0且 、
、 不共线;特别地:
不共线;特别地: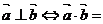 0
0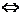 x1 x2+y1 y2=0;
x1 x2+y1 y2=0;
O是⊿ABC的垂心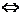
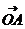 ·
·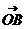 =
=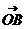 ·
·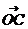 =
=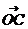 ·
·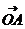 (请读者证明这个结论)。
(请读者证明这个结论)。
(2)长度: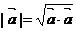 即∣
即∣ ∣2=(
∣2=( )2(符号运算);∣
)2(符号运算);∣ ∣2=x12+y12 (坐标运算)。
∣2=x12+y12 (坐标运算)。
 ⊥
⊥
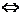 |
| -
- |=|
|=| +
+ |(矩形),(
|(矩形),( -
- )⊥(
)⊥( +
+ )
)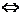 |
| |=|
|=| |(菱形),
|(菱形),
| -
- |2+|
|2+| +
+ |2=2(|
|2=2(| |2+|
|2+| |2)(即平行四边形对角线的平方和等于四条边的平方和,对已知三角形三边长求中线长的问题用这个结论很快捷)。
|2)(即平行四边形对角线的平方和等于四条边的平方和,对已知三角形三边长求中线长的问题用这个结论很快捷)。
[举例1]已知 =(1,0),
=(1,0), =(0,1),求使向量
=(0,1),求使向量 +k
+k 与向量
与向量 +2k
+2k 的夹角为锐角的k的取值范围。
的夹角为锐角的k的取值范围。
解析: +k
+k =(1,k),
=(1,k), +2k
+2k =(2k,1),向量
=(2k,1),向量 +k
+k 与向量
与向量 +2k
+2k 的夹角为锐角
的夹角为锐角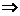
( +k
+k )(
)( +2k
+2k )>0,且
)>0,且 +k
+k 与
与 +2k
+2k 不共线,即2k+k>0且2k2≠1得:k>0,且k
不共线,即2k+k>0且2k2≠1得:k>0,且k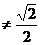 。
。
[举例2]已知向量 =(cos
=(cos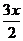 ,sin
,sin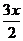 ),
), =(cos
=(cos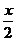 ,-sin
,-sin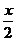 ),且x∈[
),且x∈[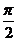 ,
,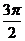 ].
].
(1) 求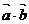 及|
及| +
+ |;(II)求函数f(x)=
|;(II)求函数f(x)=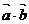 -
-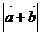 的最小值。
的最小值。
解析:(Ⅰ)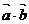 = cos
= cos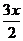 cos
cos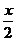 -sin
-sin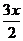 sin
sin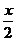 =cos2x (坐标运算),
=cos2x (坐标运算),
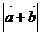 =
=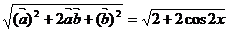 = -2cosx(符号运算);
= -2cosx(符号运算);
(Ⅱ)f(x)= cos2x +2cosx =2 cos2x+2cosx-1=2(cosx+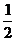 )2
)2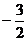 , cosx∈[-1,0]
, cosx∈[-1,0]
当cosx =0时f(x)取得最小值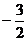 。
。
[巩固1]已知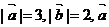 与
与 的夹角为60°,如果
的夹角为60°,如果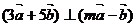 ,则m的值为( )A.
,则m的值为( )A.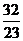 B.
B.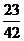 C.
C.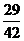 D.
D.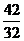
[巩固2] 已知△OFQ的面积为S,且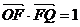 ,(1)若
,(1)若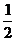 <S<2,求向量
<S<2,求向量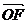 与
与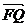 的夹角θ的取值范围; (2)设|
的夹角θ的取值范围; (2)设|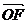 |=
|=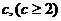 ,S =
,S =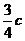 ,若以O为中心,F为焦点的椭圆经过点Q,当|
,若以O为中心,F为焦点的椭圆经过点Q,当|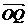 |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
[迁移] 已知非零向量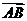 与
与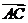 满足
满足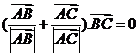 且
且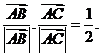 则
则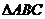 为( )
为( )
(A)等边三角形(B)直角三角形 (C)等腰非等边三角形 (D)三边均不相等的三角形
2.在 ≠0时,
≠0时, ∥
∥ (即
(即 、
、 共线)
共线)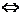 存在实常数
存在实常数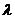 使
使 =
=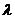
 (特别地:当
(特别地:当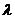 >0时同向,当
>0时同向,当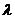 <0时反向);若
<0时反向);若 =(x1,y1),
=(x1,y1),  =(x2,y2),则
=(x2,y2),则 ∥
∥
 x1y2=x2y1(“共线”的坐标表示)。引申:若A、B、P三点共线,则
x1y2=x2y1(“共线”的坐标表示)。引申:若A、B、P三点共线,则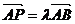 ;拓展:若
;拓展:若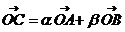 则A、B、C共线当且仅当
则A、B、C共线当且仅当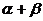 =1。[关注]
=1。[关注]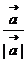 表示与向量
表示与向量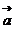 同向的单位向量,
同向的单位向量,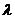 (
(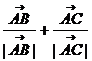 ),
),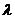 >0表示∠BAC的平分线。
>0表示∠BAC的平分线。
[举例]设 、
、 是两个起点相同且不共线的非零向量,则当实数t=______时,
是两个起点相同且不共线的非零向量,则当实数t=______时, ,t
,t ,
,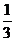 (
( +
+ )三向量的终点共线
)三向量的终点共线
解析:记 =
=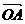 ,t
,t =
=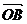 ,
,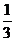 (
( +
+ )=
)=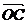 ,A、B、C三点共线即向量
,A、B、C三点共线即向量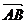 、
、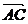 共线
共线 存在实数
存在实数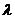 ,使得
,使得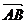 =
=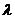
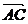 即:t
即:t -
- =
=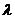 (
(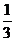
 -
-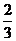
 ),∵
),∵ 、
、 不共线(很重要!)
不共线(很重要!)
∴t=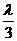 且1=
且1=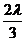
 t=
t=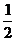 。注意:若
。注意:若 、
、 不共线的非零向量,且m
不共线的非零向量,且m +n
+n =p
=p +q
+q 则:
则:
M=n且p=q(m,n,p,q是实数),读者可以思考一下为什么?
[巩固]非零向量 =(sin
=(sin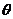 ,1),
,1),  =(0,cos
=(0,cos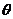 ),
), -
- 所在的直线的倾角为
所在的直线的倾角为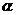 ,(1)若
,(1)若 与
与 共线,求
共线,求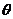 的值;(2)当
的值;(2)当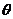 ∈(0,
∈(0,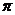 )时,求证:
)时,求证: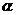 =
=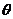 /2 。
/2 。
[迁移]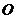 是平面上一定点,
是平面上一定点,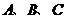 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点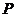 满足:
满足: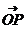 =
=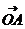 +
+
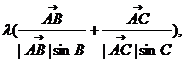 则P点的轨迹一定通过△ABC的的轨迹一定通过△ABC的
则P点的轨迹一定通过△ABC的的轨迹一定通过△ABC的
(A)外心 (B)内心 (C)重心 (D)垂心
1.向量加法的几何意义:起点相同时适用平行四边形法则(对角线),首尾相接适用“蛇形法则”(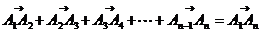 ),
),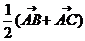 表示
表示 ABC的边BC的中线。向量减法的几何意义:起点相同适用三角形法则,(终点连结而成的向量,指向被减向量),|
ABC的边BC的中线。向量减法的几何意义:起点相同适用三角形法则,(终点连结而成的向量,指向被减向量),|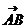 |表示A、B两点间的距离;以
|表示A、B两点间的距离;以 、
、 为邻边的平行四边形的两条对角线长分别为|
为邻边的平行四边形的两条对角线长分别为| +
+ |、|
|、| -
- |。
|。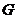 是
是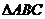 的重心
的重心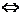
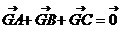 。会用“模不等式”:||
。会用“模不等式”:|| |-|
|-| ||≤
||≤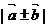 ≤|
≤| |+|
|+| |解决有关模的范围问题,关注等号成立的条件。
|解决有关模的范围问题,关注等号成立的条件。
[举例1] 已知△ABC的三个顶点A、B、C及其所在平面内一点P,满足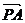 +
+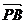 +
+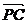 =
=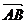 ,则点P与△ABC的关系为:
,则点P与△ABC的关系为:
A. P在△ABC内部 B. P在△ABC外部
C. P在边AB所在的直线上 D. P是AC边的一个三等分点
解析:由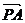 +
+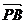 +
+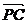 =
=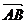
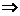
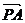 +
+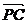 =
=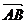 +
+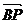
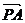 +
+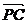 =
=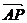
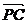 =-2
=-2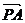
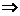 P与A、C共线且为线段AC的三等分点,选D。
P与A、C共线且为线段AC的三等分点,选D。
[举例2]已知 =(3,4),
=(3,4),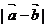 =1,则|
=1,则| |的取值范围是__________
|的取值范围是__________
解析:思路一:用“模不等式” 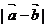 ≥||
≥|| |-|
|-| ||
||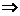 |5-|
|5-| ||≤1
||≤1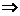 |
| |∈[4,6]。
|∈[4,6]。
思路二:记 =
=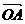 ,
, =
=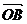 ,则A(3,4),
,则A(3,4),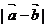 =|
=|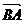 |=1,即点B到定点A的距离为1,∴点B在以A为圆心,1为半径的圆周上,数形结合不难得到|
|=1,即点B到定点A的距离为1,∴点B在以A为圆心,1为半径的圆周上,数形结合不难得到|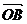 |∈[4,6],即|
|∈[4,6],即| |∈[4,6]。
|∈[4,6]。
[巩固] 已知⊿ABC,若对任意t∈R,|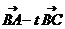 |≥|
|≥|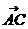 |,则
|,则
A.∠A=900 B.∠B=900 C.∠C=900 D.∠D=900
[迁移]已知向量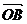 =(2,0),向量
=(2,0),向量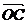 =(2,2),向量
=(2,2),向量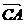 =(
=(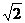 cos
cos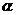 ,
,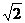 sin
sin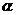 ),则向量
),则向量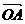 与向量
与向量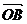 的夹角范围为:(A) [0,
的夹角范围为:(A) [0,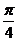 ] (B) [
] (B) [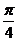 ,
,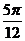 ] (C) [
] (C) [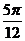 ,
,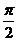 ] (D) [
] (D) [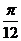 ,
,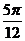 ]
]
24.请根据下面的信息,为主持人介绍的这位专家写一段正规的简历。(5分)
在一个文学座谈会上,主持人徐先生向大家这样介绍了一位专家:
“今天请大家认识一位朋友,是我的朋友,也是大家的朋友了。别看年轻,1962年的,可是得到过咱们国内有名的专家王宏庆先生真传的,是他的关门弟子。现在已经带研究生了,就在咱们河洛大学。我这位朋友写过好几本书,是专门研究曹雪芹的,有《雪芹家世考》,《<红楼梦>导读》,这本书还在“优秀教育图书”评选中获过奖呢,还有《大观园人物论》,都发行到国外了,评价很高。忘了介绍名字了,和我一个性,单字名兵,性格开朗,从小家里当男孩子看,家住冰城松花江边。”
要求:①内容适当 ②语言力求雅致得体。③字数不超过80字。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com