
7. 在等比数列{an}(n∈N*)中,已知a1>1,q>0.设bn=log2an,且b1+b3+b5=6,b1b3b5=0.
(1)求数列{an}、{bn}的通项公式an、bn;
(2)若数列{bn}的前n项和为Sn,试比较Sn与an的大小.
6. 从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少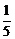 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加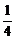 .
.
(1)设n年内(本年度为第一年)总投入为an万元,旅游业总收入为bn万元,写出an,bn的表达式;
(2)至少经过几年,旅游业的总收入才能超过总投入?
5.某种汽车购车费用10万元,每年应交保险费、养路费及汽油费合计9千元,汽车的维修费平均为第一年2千元,第二年4千元,第三年6千元,…,各年的维修费平均数组成等差数列,问这种汽车使用多少年报废最合算(即使用多少年时,年平均费用最少)?
4.已知数列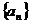 的相邻两项
的相邻两项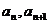 是关于
是关于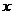 的方程
的方程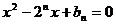
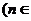 N
N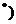 的两根,且
的两根,且
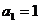 .
.
(1) 求证: 数列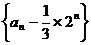 是等比数列;
是等比数列;
(2) 求数列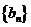 的前
的前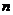 项和
项和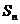 .
.
3. 已知数列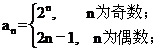 , 求
, 求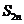
2.数列{an}中,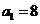 ,
,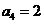 ,且满足
,且满足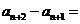 常数
常数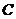
(1)求常数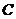 和数列的通项公式;
和数列的通项公式;
(2)设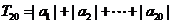 ,
,
(3) 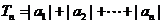 ,
,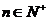
1. 已知数列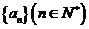 是等比数列,且
是等比数列,且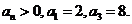
(1)求数列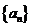 的通项公式;
的通项公式;
(2)求证: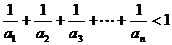 ;
;
(3)设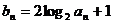 ,求数列
,求数列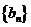 的前100项和.
的前100项和.
一个士兵,非常不善于长跑,所以在一次部队的越野赛中很快就远落人后,一个人孤零零地跑着。转过了几道弯,遇到了一个岔路口,一条路,标明是军官跑的;另一条路,标明是士兵跑的小径。他停顿了一下,虽然对做军官连越野赛都有便宜可沾感到不满,但是仍然朝着士兵的小径跑去。没想到过了半个小时后到达终点,却是名列第一。他感到不可恩议,自己从来没有取得过名次不说,连前50名也没有跑过。但是,主持赛跑的军官笑着恭喜他取得了比赛的胜利。过了几个钟头后,大批人马到了,他们跑得筋疲力尽,看见他赢得了胜利,也觉得奇怪。但是突然大家醒悟过来,在岔路口诚实守信,是多么重要。
这名士兵非常不善于长跑,却是名列第一,为什么?这给你什么启示?请运用所学知识谈一下你的感悟。字数控制在100字。
3、假如你购到了假的“泰国香米”,你会怎样做?(4分)
2、作为一个聪明的消费者,应怎样避免权利受到侵犯?(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com