
3.下列各句中,加点的词语使用有误的一句是
A.柳永词抒发的是大众情感,他要搜刮大众人人心中所有的东西变成歌词,然后再得到他们的喝彩。
B.难得的一个假日,他花了将近四个小时,忙出一身大汗,累得直不起腰,终于将书柜里的书归整了一番。
C.“神舟”七号飞船的船舱里,安装了几十件极精密的仪器设备,简直就是一个“太空实验室”。 D.记者在采访时发现,这个饭店洗手间的毛巾、手纸等经常被一些缺少公共道德的顺理成章地占为己有。
2.下列词语中没有错别字的一组是
A.目前海峡两岸面临着抵御全球金融危机的共同任务和挑战,两岸更应该加强沟通,积极推动互会互利的合作,努力化挑战为机遇。
B.要妥善处理优先发展与量力而行的关系,避免盲目上项目和过渡负债,要正确处理办学规模与办学质量的关系,坚持内含式发展。
C.至少在短期之内,不要指望中国能为遏制正在全球蔓延的经济衰竭起很大作用,这并不是说中国故意逃避责任,也不是对中国的经济前景感到悲观。
D.几只隽逸的在鳞鳞如觳纹的湖面横掠着,小燕子的剪尾或翼尖,偶沾了水面一下,那小圆晕便一圈一圈地荡漾了开去。
(湖南省衡阳市2008/2009学年度高三联合考试)
1.下列词语中加点的字,读音全都正确的一组是
A.讣告 fù 杵臼 xǔ 煲汤 bāo 同仇敌忾kài
B.侪辈 chái 绾结 wǎn 揆度 kuí 韦编三绝wéi
C.刹那 chà 愆期 yǎn 蓦地 mò 含英咀华jǔ
D.霰雪 xiàn 旌表 jīnɡ 睇眄 ɡài 翘首而待qiáo
7.(本小题满分12分)
已知数列
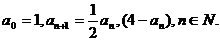
(1)证明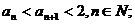
(2)求数列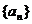 的通项公式an.
的通项公式an.
解:(1)方法一 用数学归纳法证明:
1°当n=1时,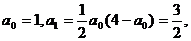
∴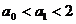 ,命题正确.
,命题正确.
2°假设n=k时有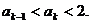
则
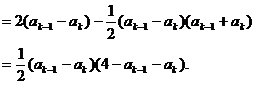
而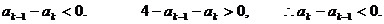
又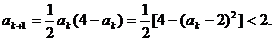
∴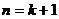 时命题正确.
时命题正确.
由1°、2°知,对一切n∈N时有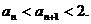
方法二:用数学归纳法证明:
1°当n=1时,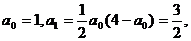 ∴
∴ ;
;
2°假设n=k时有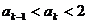 成立,
成立,
令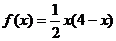 ,
,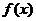 在[0,2]上单调递增,所以由假设
在[0,2]上单调递增,所以由假设
有: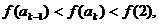 即
即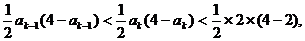
也即当n=k+1时 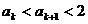 成立,所以对一切
成立,所以对一切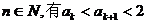
(2)下面来求数列的通项: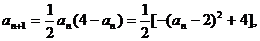 所以
所以
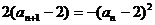
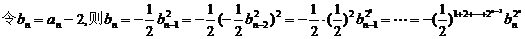 ,
,
又bn=-1,所以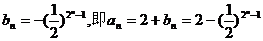
6.(本小题满分12分)
数列{an}满足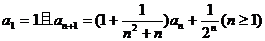 .
.
(Ⅰ)用数学归纳法证明: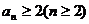 ;
;
(Ⅱ)已知不等式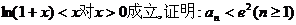 ,其中无理数e=2.71828….
,其中无理数e=2.71828….
(Ⅰ)证明:(1)当n=2时,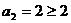 ,不等式成立.
,不等式成立.
(2)假设当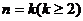 时不等式成立,即
时不等式成立,即
那么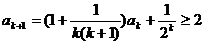 . 这就是说,当
. 这就是说,当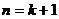 时不等式成立.
时不等式成立.
根据(1)、(2)可知: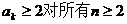 成立.
成立.
(Ⅱ)证法一:
由递推公式及(Ⅰ)的结论有 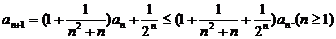
两边取对数并利用已知不等式得 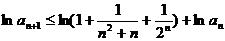
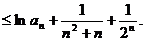 故
故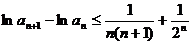
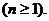
上式从1到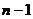 求和可得
求和可得
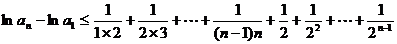
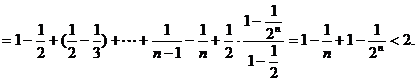
即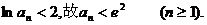
(Ⅱ)证法二:
由数学归纳法易证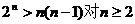 成立,故
成立,故
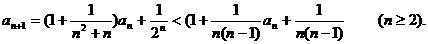
令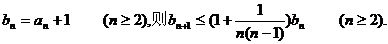
取对数并利用已知不等式得 
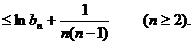
上式从2到n求和得 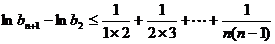
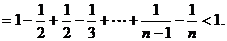
因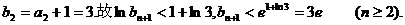
故 成立.
成立.
5.(本小题满分12分)
已知椭圆C1的方程为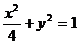 ,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(Ⅰ)求双曲线C2的方程;
(Ⅱ)若直线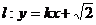 与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足
与椭圆C1及双曲线C2都恒有两个不同的交点,且l与C2的两个交点A和B满足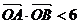 (其中O为原点),求k的取值范围.
(其中O为原点),求k的取值范围.
解:(Ⅰ)设双曲线C2的方程为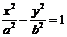 ,则
,则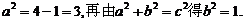
故C2的方程为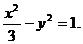
(II)将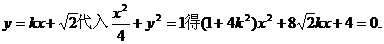
由直线l与椭圆C1恒有两个不同的交点得
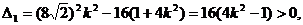
即 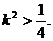 ①
①
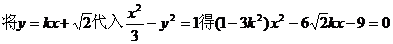 .
.
由直线l与双曲线C2恒有两个不同的交点A,B得
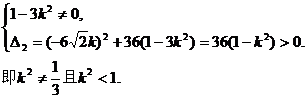

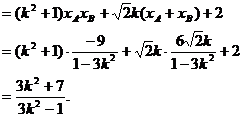
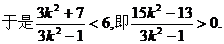 解此不等式得
解此不等式得
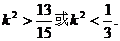 ③
③
由①、②、③得
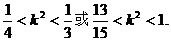
故k的取值范围为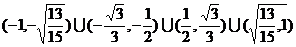
4.(本小题满分14分)
已知动圆过定点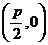 ,且与直线
,且与直线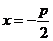 相切,其中
相切,其中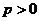 .
.
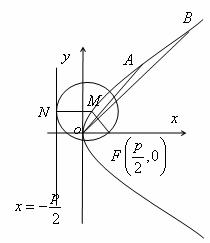
(I)求动圆圆心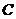 的轨迹的方程;
的轨迹的方程;
(II)设A、B是轨迹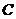 上异于原点
上异于原点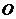 的两个不同点,直线
的两个不同点,直线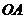 和
和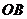 的倾斜角分别为
的倾斜角分别为 和
和 ,当
,当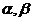 变化且
变化且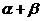 为定值
为定值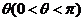 时,证明直线
时,证明直线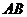 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
解:(I)如图,设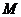 为动圆圆心,
为动圆圆心,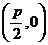 为记为
为记为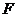 ,过点
,过点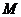 作直线
作直线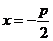 的垂线,垂足为
的垂线,垂足为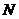 ,由题意知:
,由题意知: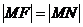 即动点
即动点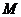 到定点
到定点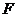 与定直线
与定直线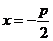 的距离相等,由抛物线的定义知,点
的距离相等,由抛物线的定义知,点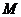 的轨迹为抛物线,其中
的轨迹为抛物线,其中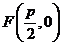 为焦点,
为焦点,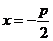 为准线,所以轨迹方程为
为准线,所以轨迹方程为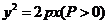 ;
;
(II)如图,设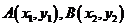 ,由题意得
,由题意得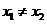 (否则
(否则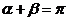 )且
)且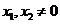 所以直线
所以直线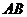 的斜率存在,设其方程为
的斜率存在,设其方程为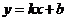 ,显然
,显然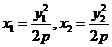 ,将
,将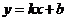 与
与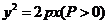 联立消去
联立消去 ,得
,得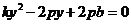 由韦达定理知
由韦达定理知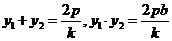 ①
①
(1)当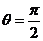 时,即
时,即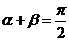 时,
时, 所以
所以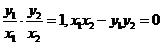 ,
,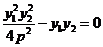 所以
所以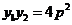 由①知:
由①知: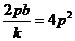 所以
所以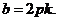 因此直线
因此直线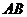 的方程可表示为
的方程可表示为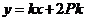 ,即
,即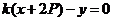 所以直线
所以直线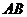 恒过定点
恒过定点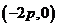
(2)当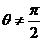 时,由
时,由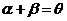 ,得
,得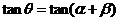 =
=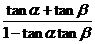 =
=
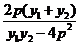 将①式代入上式整理化简可得:
将①式代入上式整理化简可得: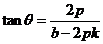 ,所以
,所以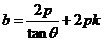 ,
,
此时,直线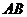 的方程可表示为
的方程可表示为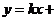
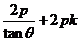 即
即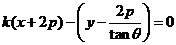
所以直线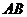 恒过定点
恒过定点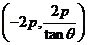
所以由(1)(2)知,当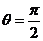 时,直线
时,直线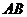 恒过定点
恒过定点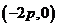 ,当
,当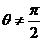 时直线
时直线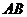 恒过定点
恒过定点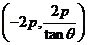 .
.
3.(本小题满分12分)
已知数列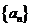 的首项
的首项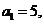 前
前 项和为
项和为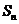 ,且
,且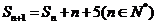
(I)证明数列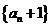 是等比数列;
是等比数列;
(II)令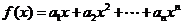 ,求函数
,求函数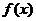 在点
在点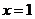 处的导数
处的导数 并比较
并比较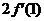 与
与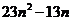 的大小.
的大小.
解:由已知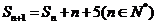 可得
可得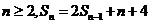 两式相减得
两式相减得
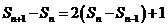 即
即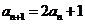 从而
从而 当
当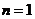 时
时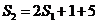 所以
所以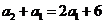 又
又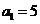 所以
所以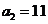 从而
从而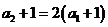
故总有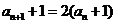 ,
,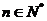 又
又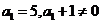 从而
从而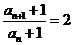 即数列
即数列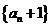 是等比数列;
是等比数列;
(II)由(I)知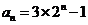
因为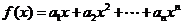 所以
所以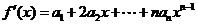
从而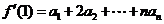 =
=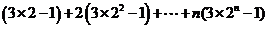
=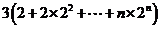 -
-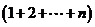 =
=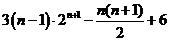
由上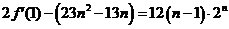 -
-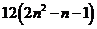 =
=
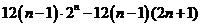 =12
=12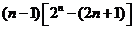 ①
①
当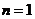 时,①式=0所以
时,①式=0所以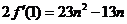 ;
;
当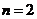 时,①式=-12
时,①式=-12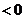 所以
所以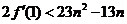
当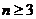 时,
时,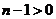
又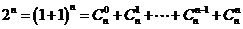
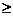
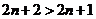
所以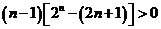 即①
即①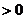 从而
从而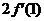
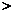
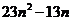
2.(本小题满分12分)
函数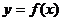 在区间(0,+∞)内可导,导函数
在区间(0,+∞)内可导,导函数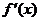 是减函数,且
是减函数,且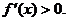 设
设
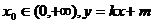 是曲线
是曲线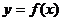 在点(
在点(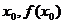 )得的切线方程,并设函数
)得的切线方程,并设函数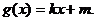
(Ⅰ)用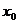 、
、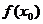 、
、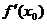 表示m;
表示m;
(Ⅱ)证明:当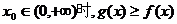 ;
;
(Ⅲ)若关于 的不等式
的不等式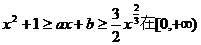 上恒成立,其中a、b为实数,
上恒成立,其中a、b为实数,
求b的取值范围及a与b所满足的关系.
本小题考查导数概念的几何意义,函数极值、最值的判定以及灵活运用数形结合的思想判断函数之间的大小关系.考查学生的学习能力、抽象思维能力及综合运用数学基本关系解决问题的能力.满分12分
(Ⅰ)解: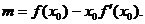 …………………………………………2分
…………………………………………2分
(Ⅱ)证明:令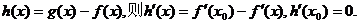
因为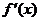 递减,所以
递减,所以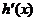 递增,因此,当
递增,因此,当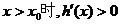 ;
;
当 .所以
.所以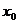 是
是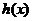 唯一的极值点,且是极小值点,可知
唯一的极值点,且是极小值点,可知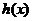 的
的
最小值为0,因此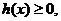 即
即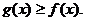 …………………………6分
…………………………6分
(Ⅲ)解法一: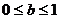 ,
,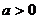 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
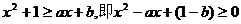 对任意
对任意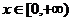 成立的充要条件是
成立的充要条件是
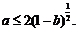
另一方面,由于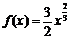 满足前述题设中关于函数
满足前述题设中关于函数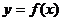 的条件,利用(II)的结果可知,
的条件,利用(II)的结果可知,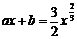 的充要条件是:过点(0,
的充要条件是:过点(0,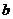 )与曲线
)与曲线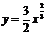 相切的直线的斜率大于
相切的直线的斜率大于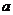 ,该切线的方程为
,该切线的方程为
于是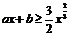 的充要条件是
的充要条件是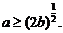 …………………………10分
…………………………10分
综上,不等式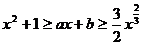 对任意
对任意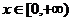 成立的充要条件是
成立的充要条件是
 ①
①
显然,存在a、b使①式成立的充要条件是:不等式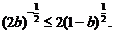 ②
②
有解、解不等式②得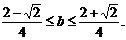 ③
③
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
(Ⅲ)解法二: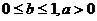 是不等式成立的必要条件,以下讨论设此条件成立.
是不等式成立的必要条件,以下讨论设此条件成立.
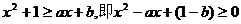 对任意
对任意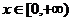 成立的充要条件是
成立的充要条件是
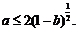 ………………………………………………………………8分
………………………………………………………………8分
令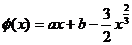 ,于是
,于是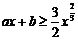 对任意
对任意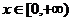 成立的充要条件是
成立的充要条件是
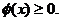 由
由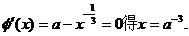
当 时
时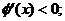 当
当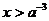 时,
时,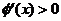 ,所以,当
,所以,当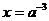 时,
时,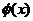 取最小值.因此
取最小值.因此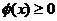 成立的充要条件是
成立的充要条件是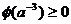 ,即
,即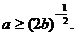 ………………10分
………………10分
综上,不等式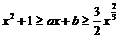 对任意
对任意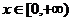 成立的充要条件是
成立的充要条件是
 ①
①
显然,存在a、b使①式成立的充要条件是:不等式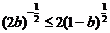 ②
②
有解、解不等式②得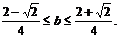
因此,③式即为b的取值范围,①式即为实数在a与b所满足的关系.…………12分
1.(本小题满分14分)
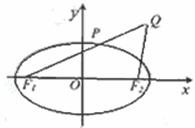
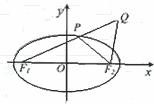
已知椭圆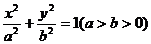 的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足
的左、右焦点分别是F1(-c,0)、F2(c,0),Q是椭圆外的动点,满足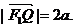 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足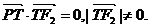
(Ⅰ)设 为点P的横坐标,证明
为点P的横坐标,证明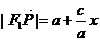 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,使△F1MF2的面积S=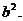 若存在,求∠F1MF2的正切值;若不存在,请说明理由.
若存在,求∠F1MF2的正切值;若不存在,请说明理由.
本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应用,以及综合运用数学知识解决问题的能力.满分14分.
(Ⅰ)证法一:设点P的坐标为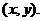
由P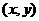 在椭圆上,得
在椭圆上,得
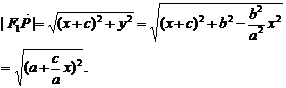
由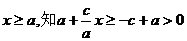 ,所以
,所以 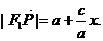 ………………………3分
………………………3分
证法二:设点P的坐标为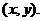 记
记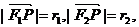
则
由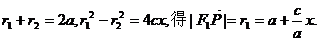
证法三:设点P的坐标为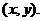 椭圆的左准线方程为
椭圆的左准线方程为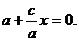
由椭圆第二定义得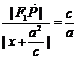 ,即
,即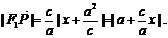
由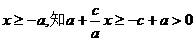 ,所以
,所以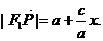 …………………………3分
…………………………3分
(Ⅱ)解法一:设点T的坐标为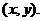
当 时,点(
时,点(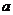 ,0)和点(-
,0)和点(-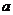 ,0)在轨迹上.
,0)在轨迹上.
当|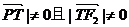 时,由
时,由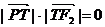 ,得
,得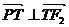 .
.
又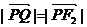 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,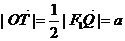 ,所以有
,所以有
综上所述,点T的轨迹C的方程是 …………………………7分
…………………………7分
解法二:设点T的坐标为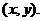 当
当 时,点(
时,点(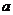 ,0)和点(-
,0)和点(-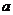 ,0)在轨迹上.
,0)在轨迹上.
当|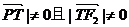 时,由
时,由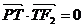 ,得
,得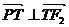 .
.
又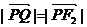 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为( ),则
),则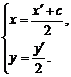
因此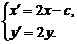 ①
①
由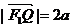 得
得 ②
②
将①代入②,可得
综上所述,点T的轨迹C的方程是 ……………………7分
……………………7分
|
 )使S=
)使S=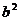 的充要条件是
的充要条件是
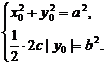
由③得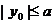 ,由④得
,由④得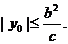 所以,当
所以,当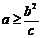 时,存在点M,使S=
时,存在点M,使S=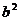 ;
;
当 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当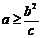 时,
时,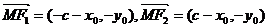 ,
,
由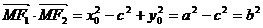 ,
,
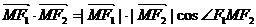 ,
,
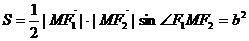 ,得
,得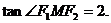
解法二:C上存在点M( )使S=
)使S=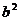 的充要条件是
的充要条件是
|
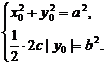
由④得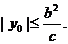 上式代入③得
上式代入③得
于是,当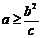 时,存在点M,使S=
时,存在点M,使S=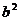 ;
;
当 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当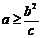 时,记
时,记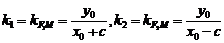 ,
,
由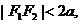 知
知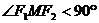 ,所以
,所以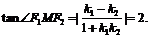 …………14分
…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com