
20.(本小题满分12分)已知数列{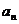 }中
}中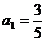 ,
,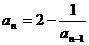 (n≥2,
(n≥2,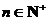 ),数列
),数列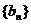 ,满足
,满足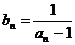 (
(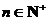 )
)
(1)求证数列{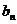 }是等差数列;
}是等差数列;
(2)若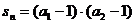 +
+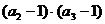 +
+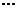
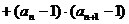
是否存在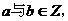 使得:
使得: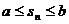 恒成立.若有,求出
恒成立.若有,求出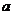 的最大值与
的最大值与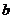 的最小值,如果没有,请说明理由.
的最小值,如果没有,请说明理由.
19.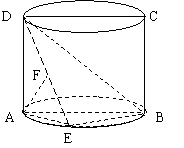 (本小题满分12分)如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
(本小题满分12分)如图,圆柱的轴截面ABCD是正方形,点E在底面圆周上,点F在DE上,且AF⊥DE,若圆柱的侧面积与△ABE的面积之比等于4π.
(1)求证:AF⊥BD;
(2)求二面角A―BD―E的正弦值.
k*s*5*u
18.(本小题满分12分)已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球。现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望。
17.(本小题满分12分)已知函数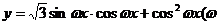 >0)的周期为
>0)的周期为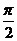 .
.
(1)求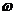 的值;
的值;
(2)当0≤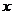 ≤
≤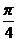 时,求函数的最大值和最小值以及相应的
时,求函数的最大值和最小值以及相应的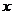 的值.
的值.
16、设命题p:|4x-3|≤1;
命题q: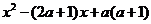 ≤0.
≤0.
若﹁ p是﹁ q的必要而不充分的条件,则实数a的取值范围是
k*s*5*u
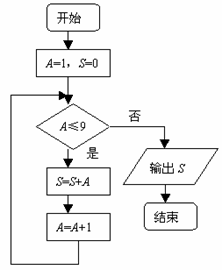
15、.如图,该程序运行后输出的结果为
14、已知函数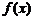 满足:
满足: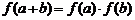 ,
,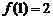 ,
,
则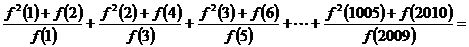
13、若不等式组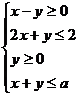 表示的平面区域是一个三角形,则a的取值范围是
表示的平面区域是一个三角形,则a的取值范围是
12、定义在R上的函数y=f(x)在(-∞,2)上是增函数,且函数y=f(x+2)的图象的对称轴是直线x=0,则
(A) f(-1)<f(3) (B) f(0)>f(3) (C) f(-1)=f(3) (D) f(2)<f(3).
第Ⅱ卷(非选择题 共90分)
11、如图,要测量河对岸A、B两点间的距离,今沿河岸选取相距40米的C、D两点,测得 ∠ACB=60°,∠BCD=45°,∠ADB=60°,∠ADC=30°,则AB的距离是.
(A)20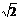 (B)20
(B)20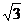 (C)40
(C)40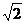 (D)20
(D)20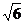
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com